
Bue (geometri) mål, buetyper, eksempler
De Bue, i geometri er det en hvilken som helst buet linje som forbinder to punkter. En buet linje, i motsetning til en rett linje, er en hvis retning er forskjellig på hvert punkt på den. Det motsatte av en bue er et segment, siden dette er en rett seksjon som forbinder to punkter.
Buen som oftest brukes i geometri er omkretsbuen. Andre buer i vanlig bruk er parabolbuen, elliptisk buen og ledningsbuen. Bueformen brukes også ofte i arkitektur som et dekorativt element og et strukturelt element. Dette er tilfellet med overligger på dører og vinduer, så vel som broer og akvedukter.

Artikkelindeks
- 1 Buen og dens mål
- 2 Typer buer
- 2.1 Sirkelbue
- 2.2 Parabolsk bue
- 2.3 Ledningsbue
- 2.4 Elliptisk bue
- 3 Eksempler på buer
- 3.1 Eksempel 1
- 3.2 Eksempel 2
- 4 Referanser
Buen og dens mål
Målene på en bue er lengden, som avhenger av kurvetypen som forbinder de to punktene og deres plassering..
Lengden på en sirkelbue er en av de enkleste å beregne, fordi lengden på hele buen eller omkretsen av en omkrets er kjent.
Omkretsen til en sirkel er to pi ganger radioen din: p = 2 π R. Å vite dette, hvis du vil beregne lengden s av en sirkulær vinkelbue α (målt i radianer) og radius R, det brukes et forhold:
(s / p) = (α / 2 π)
Så rydding s fra forrige uttrykk og erstatte omkretsen s ved sitt uttrykk som en funksjon av radiusen R, du har:
s = (α / 2 π) p = (α / 2 π) (2 π R) = α R.
Det vil si at målingen på en sirkelbue er produktet av dens vinkelåpningstid radien til den sirkulære buen.
For en bue generelt er problemet mer komplisert, til det punktet at antikkens store tenkere bekreftet at det var en umulig oppgave..
Det var ikke før adventen av differensial- og integralkalkulus i 1665, at problemet med måling av en hvilken som helst lysbue ble løst tilfredsstillende.
Før oppfinnelsen av differensialregning, kunne løsninger bare bli funnet ved å bruke polygonale linjer eller buer med omkrets som nærmet seg den virkelige buen, men disse løsningene var ikke eksakte.
Typer buer
Fra et geometrisk synspunkt klassifiseres buer i henhold til den buede linjen som forbinder to punkter på planet. Det er andre klassifiseringer i henhold til deres bruk og arkitektoniske form.
Sirkulær bue
Når linjen som forbinder to punkter i planet, er et stykke omkrets med en viss radius, har vi en sirkelbue. Figur 2 viser en sirkelbue c med radius R-forbindelsespunktene A og B.
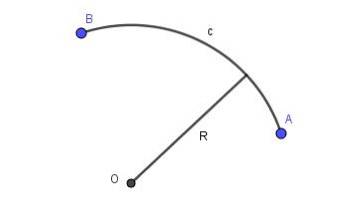
Parabolsk bue
Parabolen er stien fulgt av et objekt som er kastet skrått i luften. Når kurven som forbinder to punkter er en parabel, har vi en parabolbue som den som er vist i figur 3.
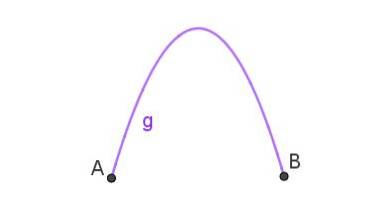
Dette er formen på vannstrålen som kommer ut av en slange som peker oppover. Parabolbuen kan observeres i vannkildene.

Koblingsbue
Koblingsbuen er en annen naturlig bue. Koblingsledningen er kurven som dannes naturlig når en kjede eller et tau henger løst fra to separate punkter.
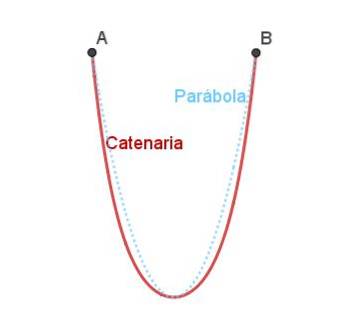
Koblingsledningen ligner parabolen, men den er ikke akkurat den samme som kan sees i figur 4.
Den omvendte ledningsbuen brukes i arkitekturen som et strukturelt element med høy trykkfasthet. Faktisk kan det vises at den er den sterkeste typen bue av alle mulige former..
For å bygge en solid ledningsbue, er det bare å kopiere formen på et hengende tau eller en kjede, så blir den kopierte formen snudd for å reprodusere den på døren eller vinduskarmen.
Elliptisk bue
En bue er elliptisk hvis kurven som forbinder to punkter, er et stykke eller en del av en ellips. Ellipsen er definert som stedet for punktene hvis avstand til to gitte punkter alltid gir en konstant størrelse.
Ellipsen er en kurve som vises i naturen: det er kurven til planetenes bane rundt solen, som demonstrert av Johannes Kepler i år 1609.
I praksis kan en ellipse tegnes ved å feste to stiver på bakken eller to pinner på papir og binde en streng til dem. Tauet blir deretter spent med markøren eller blyanten, og kurven blir sporet. Et stykke ellips er en elliptisk lysbue. Følgende animasjon illustrerer hvordan ellipsen tegnes:
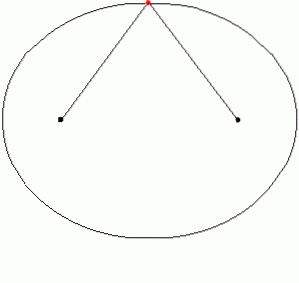
Figur 6 viser et elliptisk lysbueforbindelsespunkt G og H.
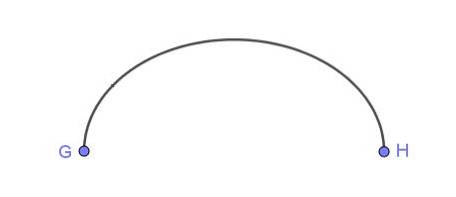
Eksempler på buer
Følgende eksempler refererer til hvordan man beregner omkretsen til noen spesifikke buer.
Eksempel 1
Figur 7 viser et vindu ferdig i en kuttet sirkelbue. Dimensjonene vist i figur er i fot. Beregn lengden på buen.
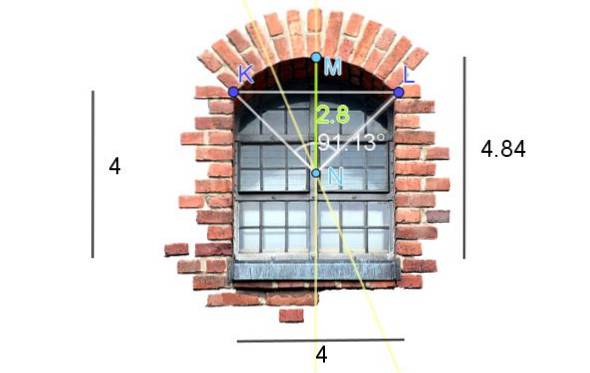
For å få sentrum og radius av den runde buen til vindusoverligningen, er følgende konstruksjoner laget på bildet:
-Segmentet KL er tegnet og halveringen tegnet.
-Etterpå ligger det høyeste punktet på overliggeren, som vi kaller M. Deretter blir segmentet vurdert og dens mediatrix spores..
Skjæringspunktet til de to halveringslinjene er punkt N, og det er også sentrum for sirkelbuen.
-Nå må vi måle lengden på segmentet NM, som sammenfaller med radien R for sirkelbuen: R = 2,8 fot.
-For å kjenne lengden på buen i tillegg til radiusen, er det nødvendig å kjenne vinkelen som buen danner. Som kan bestemmes ved to metoder, enten måles det med en vinkelmåler, eller alternativt beregnes den ved hjelp av trigonometri.
I det viste tilfellet er vinkelen dannet av buen 91,13 º, som må konverteres til radianer:
91,13º = 91,13º * π / 180º = 1,59 radianer
Til slutt beregner vi lengden s av buen ved hjelp av formelen s = α R.
s = 1,59 * 2,8 fot = 4,45 fot
Eksempel 2
Finn lengden på den elliptiske buen som er vist i figur 8, og kjenn den halv-store aksen r og den semi-mindre aksen s av ellipsen.
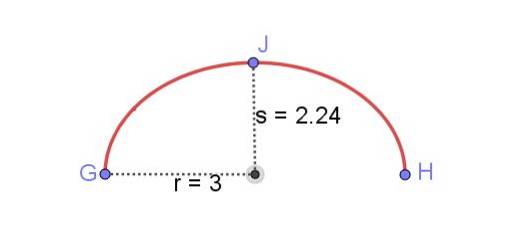
Å finne lengden på en ellips var et av de vanskeligste problemene i matematikk i lang tid. Du kan få løsninger uttrykt ved elliptiske integraler, men for å ha en numerisk verdi må du utvide disse integralene i kraftserier. Et nøyaktig resultat vil kreve uendelige vilkår for disse seriene.
Heldigvis fant det hinduiske matematiske geniet Ramanujan, som levde mellom 1887 og 1920, en formel som veldig nøyaktig tilnærmer seg omkretsen til en ellips:
Omkrets av en ellips = π [3 (r + s) - √ ((3r + s) (r + 3s))]
Omkretsen til en ellips med r = 3 cm og s = 2,24 cm er 16,55 cm. Den viste elliptiske buen har imidlertid halvparten av denne verdien:
Lengde på elliptisk bue GH = 8,28 cm.
Referanser
- Clemens S. 2008. Geometri og trigonometri. Pearson Education.
- García F. Numeriske prosedyrer i Java. Lengde på en ellips. Gjenopprettet fra: sc.ehu.es
- Dynamisk geometri. Buer. Gjenopprettet fra geometriadinamica.es
- Piziadas. Ellipser og paraboler rundt oss. Gjenopprettet fra: piziadas.com
- Wikipedia. Bue (geometri). Gjenopprettet fra: es.wikipedia.com


Ingen har kommentert denne artikkelen ennå.