
Poissons forhold, formler, verdier, eksempler
De Poissons forhold det er en dimensjonsløs mengde, karakteristisk for hvert materiale. Det er en indikasjon på deformasjonen av et stykke materiale før påføring av visse krefter.
Når et stykke materiale som er utsatt for en spenning, eller en kompresjon, gjennomgår en deformasjon, er kvotienten mellom den tverrgående deformasjonen og den langsgående deformasjonen nøyaktig Poissons forhold.
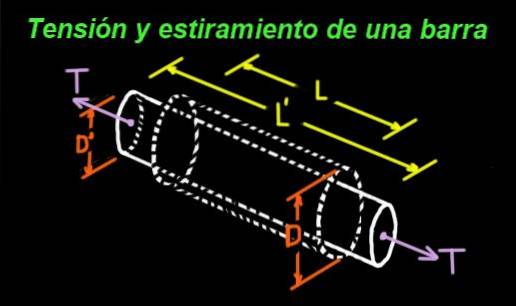
For eksempel strekker en gummisylinder som er stresset i endene i lengderetningen, men smalner på tvers. Figur 1 viser en stang med originale dimensjoner: lengde L og diameter D.
Stangen utsettes for en spenning T i endene, og som en konsekvens av denne spenningen gjennomgår den en strekk, slik at den nye lengden er L '> L. Men når den strekkes, blir dens diameter også smalere til den nye verdien: D' < D.
Kvotienten mellom strekningen (positiv) og innsnevringen (negativ) multiplisert med (-1), er et positivt tall mellom 0 og 0,5. Dette tallet er det såkalte Poissons forholdet ν (gresk bokstav nu).
Artikkelindeks
- 1 Poissons forholdsformel
- 1.1 Forholdet til elastisitetsmodulen og stivhetsmodulen
- 2 Verdi av Poissons forhold for materialer
- 3 Beregningseksempler
- 3.1 Eksempel 1
- 3.2 Eksempel 2
- 4 Referanser
Poissons forholdsformel
For å beregne Poissons forhold er det nødvendig å bestemme den langsgående og tverrgående belastningen.
Den langsgående belastningen εL er strekningen delt på den opprinnelige lengden:
εL = (L '- L) / L.
Tilsvarende er tverrstammen εT er den radiale konen delt på den originale diameteren:
εT = (D '- D) / D.
Derfor beregnes Poissons forhold ved hjelp av følgende formel:
ν = - εT / εL
Forhold til elastisitetsmodul og stivhetsmodul
Poissons forhold ν, er relatert til modulen OG elastisitet (eller Youngs modul) og med stivhetsmodulen G, ved hjelp av følgende formel:
ν = E / (2G) - 1
Poissons forholdsverdi for materialer


Beregningseksempler
Eksempel 1
En stang av et bestemt plastmateriale har en lengde på 150 mm og et sirkulært snitt på 20 mm i diameter. Når den utsettes for en kompresjonskraft F på 612,25 kg-f, observeres en forkortelse på 14 mm og samtidig en økning på 0,85 mm i stangens diameter.
Regne ut:
a) Lengdespenning.
b) Tverrstammen.
c) Poissons forhold til det materialet.
d) Youngs elastisitetsmodul som tilsvarer materialet.
e) Stivhetsmodulen for den plasten.
Løsning til
Husk at den langsgående belastningen εL er strekningen delt på den opprinnelige lengden:
εL = (L '- L) / L.
εL = (-14 mm) / 150 mm = -0,0933
Merk at den langsgående belastningen er dimensjonsløs, og i dette tilfellet har den vært negativ fordi det var en reduksjon i dens lengdedimensjon.
Løsning b
Tilsvarende er tverrstammen εT den radiale konen, delt på den opprinnelige diameteren:
εT = (D '- D) / D.
εT = (+0,85 mm) / 20 mm = 0,0425
Tverrstammen har vært positiv fordi det har vært en økning i stangens diameter.
Løsning c
For beregningen av Poissons forhold må vi huske at det er definert som det negative av kvotienten mellom den tverrgående deformasjonen og den langsgående deformasjonen:
ν = - εT / εL
v = - 0,0425 / (-0,0933) = 0,4554
Det skal huskes at Poissons forhold er et positivt dimensjonsløst tall, og for de fleste materialer er det mellom 0 og 0,5.
Løsning d
Youngs elastisitetsmodul, betegnet med bokstaven E, er proporsjonalitetskonstanten i Hookes lov. Ved E er den normale spenningen σL relatert til stammen εL, som følger:
σL = E εL
Den normale spenningen er definert som kvotienten mellom den normale kraften (i dette tilfellet parallelt med stangens akse) og tverrsnittsområdet:
σL = F / A = F / (π / 4 * D ^ 2)
I denne øvelsen er kraften F 612,25 kg-f, som må konverteres til newton, som er SI-kraftenheten:
F = 612,25 kg-f = 612,25 * 9,8 N = 6000 N = 6 kN
For sin del er tverrsnittet av område A:
A = (π / 4 * D ^ 2) = (3.1416 / 4) * (20 * 10 ^ -3 m) ^ 2 = 3.1416 * 10 ^ -4 m ^ 2
Til slutt er det normale spenningen på baren:
σL = F / A = 6000 N / 3.1416 * 10 ^ -4 m ^ 2 = 19.098.593 Pa = 19.098 MPa
For å beregne Youngs elastisitetsmodul løser vi for E fra Hookes lov σL = E εL:
E = σL / εL = 19,098,593 Pa / 0,0933 = 204,7 MPa
Løsning e
Stivhetsmodulen G er relatert til Youngs modul E og Poissons forhold ν ved denne formelen:
E / (2 G) = 1 + v
Derfra kan du løse for G:
G = E / (2 (1 + ν)) = 204,7 MPa / (2 (1 + 0,4554)) = 70,33 MPa
Eksempel 2
Det er en kobberkabel med en diameter på 4 mm og 1 m lang. Å vite at Youngs kobbermodul er 110 000 MPa og at Poissons forhold er 0,34, estimer strekkingen og innsnevringen i diameter som ledningen gjennomgår når en vekt på 100 kg-f henges på den..
Løsning
Først er det nødvendig å beregne den normale strekkbelastningen som vekten utøver på ledningen, etter denne formelen:
σL = F / A = F / (π / 4 * D ^ 2)
Kraften F er 980 N og tverrsnittsarealet er:
A = (π / 4 * D ^ 2) = (3.1416 / 4) * (4 * 10 ^ -3 m) ^ 2 = 1.2566 * 10 ^ -5 m ^ 2
Så er strekkbelastningen:
σL = 980 N / 1,2566 * 10 ^ -5 m ^ 2 = 77 986 000 Pa
Beregning av trådstamme
Youngs elastisitetsmodul, betegnet med bokstaven E, er proporsjonalitetskonstanten i Hookes lov som relaterer normal spenning σL til belastningen εL:
σL = E εL
Derfra kan kobbertrådens langsgående belastning løses:
εL = σL / E = 77,986 MPa / 110000 MPa = 7,09 * 10 ^ -4
Beregning av tverrstamme
På den annen side, for å kjenne tverrstammen, brukes Poissons forhold:
ν = - εT / εL
Til slutt har vi at tverrstammen er:
εT = -ν εL = - 0,34 * 7,09 * 10 ^ -4 = -2,41 * 10 ^ -4
Beregning av absolutt kabelstrekning
Til slutt, for å vite den absolutte strekningen av kabelen, må følgende forhold brukes:
ΔL = εL * L = 7,09 * 10 ^ -4 * 1 m = 7,09 * 10 ^ -4 m = 0,709 mm
Det vil si at med den vekten strakte kabelen knapt 0,709 millimeter.
Beregning av reduksjonen i diameter
For å oppnå absolutt krymping i diameter bruker vi følgende formel:
ΔD = εT * D = -2,41 * 10 ^ -4 * 4 mm = -9,64 * 10 ^ -4 mm = -0,000964 millimeter.
Denne innsnevringen i diameter er så liten at det er vanskelig å se med det blotte øye, selv målingen krever et instrument med høy presisjon..
Referanser
- Øl F ... Mekanikk av materialer. 5. Utgave. 2010. Mc Graw Hill. 1-130.
- Hibbeler R. Materialmekanikk. Åttende utgave. Prentice Hall. 2011. 3-60.
- Gere J. Mekanikk av materialer. Åttende utgave. Cengage læring. 4-220.
- Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. 6. utg. Prentice Hall. 238-242.
- Valera Negrete, J. 2005. Notater om generell fysikk. UNAM. 87-98.


Ingen har kommentert denne artikkelen ennå.