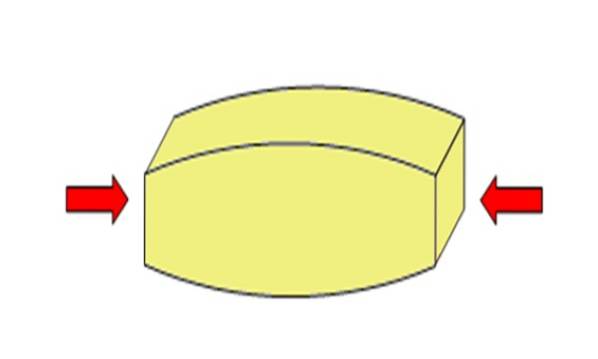
De kompresjon eller kompressionsspenning er kraften per arealeenhet hvis resultat er å presse, klemme eller komprimere en gjenstand, og har en tendens til å forkorte den. Matematisk er det:
E = F / A
Her OG betegner innsats, F størrelsen på kraften og TIL området det virker på, enheten i SI International System er newton / mto eller pascal (Pa). Kompressivt stress er en normal innsats, fordi kraften som produserer den er vinkelrett på området den utøves på.
En slik innsats kan komprimere gjenstanden eller tvert imot spenne og strekke den, slik den blir brukt. Ved kompresjonsbelastning påføres kreftene i motsatt retning for å utøve effekten av å klemme og forkorte gjenstanden..
Når kreftene opphører, går mange materialer tilbake til sine opprinnelige dimensjoner. Denne eiendommen er kjent under navnet elastisitet. Men mens det skjer, er den elastiske enhetsdeformasjonen som påføres et materiale utsatt for en påkjenning:
Stamme = (sluttstørrelse - startstørrelse) / startstørrelse
Stamme kan være lineær, overflate eller volumetrisk, selv om belastningen er uten enhet. Informasjonen den gir er imidlertid veldig viktig, siden det ikke er det samme å deformere en 10 m lang stang med 1 cm, å deformere en annen 1 m lang stang med 1 cm.
I et elastisk materiale er deformasjon og spenning proporsjonal og oppfyller Hookes lov:
Innsats Deform Enhetsdeformasjon
Artikkelindeks
Trykkbelastningen får partiklene i materialet til å komme nærmere og nærmere, og reduserer størrelsen. Avhengig av hvilken retning innsatsen påføres, vil det være en forkortelse eller reduksjon i noen av dens dimensjoner.
La oss starte med å anta en tynn stang med original lengde L, til hvilken normal belastning av størrelse OG. Hvis spenningen er komprimerende, opplever stangen en reduksjon i lengden, betegnet med δ. Hvis det er spenning, vil stangen forlenge seg.
Naturligvis er materialet som elementet er laget av avgjørende i dets evne til å motstå stress..
Disse elastiske egenskapene til materialet er inkludert i den nevnte proporsjonalitetskonstanten. Heter elastisitetsmodul eller Youngs modul og er betegnet som Y. Hvert materiale har en elastisitetsmodul, som bestemmes eksperimentelt ved laboratorietester.
Med dette i tankene, innsatsen OG Det uttrykkes i matematisk form slik:
Innsats Deform Enhetsdeformasjon
Til slutt, for å etablere denne tilstanden som en ligning, kreves en proporsjonalitetskonstant for å erstatte proporsjonalitetssymbolet ∝ og erstatte det for likhet, slik:
Stress = konstant av proporsjonalitet x enhetsstamme
E = Y. (δ / L)
Kvotienten (δ / L) er belastningen, betegnet som ε og med δ = Endelig lengde - Startlengde. På denne måten innsatsen OG ser ut som:
E = Y. ε
Siden belastning er dimensjonsløs, vil enhetene til Y er de samme som for OG: N / mto o Pa i SI-systemet, pounds / into eller psi i det britiske systemet, så vel som andre kombinasjoner av kraft og areal, som kg / cmto.
Y-verdier bestemmes eksperimentelt i laboratoriet, under kontrollerte forhold. Deretter elastisitetsmodulen for materialer som er mye brukt i konstruksjon og også for bein:
Tabell 1
| Materiale | Elastisitetsmodul Y (Pa) x 109 |
|---|---|
| Stål | 200 |
| Jern | 100 |
| Messing | 100 |
| Bronse | 90 |
| Aluminium | 70 |
| Marmor | femti |
| Granitt | Fire fem |
| Betong | tjue |
| Bein | femten |
| Furu | 10 |
Kompressorkrefter virker på forskjellige strukturer; De er underlagt virkningen av krefter som vekten til hvert av elementene som komponerer dem, så vel som krefter fra eksterne stoffer: vind, snø, andre strukturer og mer..
Det er vanlig at de fleste konstruksjoner er konstruert for å tåle påkjenninger av alle slag uten å deformere. Derfor må kompresjonsspenningen tas i betraktning for å forhindre at delen eller gjenstanden mister formen..
Også skjelettets bein er strukturer utsatt for forskjellige belastninger. Selv om beinene er motstandsdyktige mot dem, oppstår sprekker og brudd når det ved et uhell overskrides den elastiske grensen.
Byggesøyler og brygger må være laget for å motstå kompresjon, ellers har de en tendens til å bøye seg. Dette er kjent som lateral bøying eller knekk.
Kolonnene (se figur 1) er elementer hvis lengde er betydelig større enn deres tverrsnittsareal..
Et sylindrisk element er en søyle når lengden er lik eller større enn ti ganger tverrsnittets diameter. Men hvis tverrsnittet ikke er konstant, vil dets mindre diameter tas for å klassifisere elementet som en kolonne.
Når folk setter seg på møbler som stoler og benker, eller legger til gjenstander på toppen, blir bena utsatt for trykkbelastninger som har en tendens til å redusere høyden..
Møbler er vanligvis laget for å tåle vekten ganske bra og går tilbake til sin naturlige tilstand når de er fjernet. Men hvis tung vekt legges på skjøre stoler eller benker, gir bena vei til kompresjon og knusing..
Det er en stang som opprinnelig måler 12 m i lengde, og som den utsettes for et trykk på, slik at enhetsdeformasjonen er -0.0004. Hva er stangens nye lengde??
Ut fra ligningen gitt ovenfor:
ε = (δ / L) = - 0,0004
Ja LF er den endelige lengden og Leller den opprinnelige lengden, siden δ = LF - Leller du har:
(LF - Leller) / L.eller = -0.0004
Derfor: LF - Leller = -0.0004 x 12 m = -0.0048 m. Og endelig:
LF = (12 - 0,0048) m = 11,9952 m.
En solid stålstang, sylindrisk i form, er 6 m lang og 8 cm i diameter. Hvis stangen er komprimert med en last på 90.000 kg, finn:
a) Størrelsen på kompresjonsspenningen i megapascal (MPa)
b) Med hvor mye ble lengden på stangen redusert?
Først finner vi området A av tverrsnittet av stangen, som avhenger av diameteren D, noe som resulterer i:
A = π. Dto / 4 = π. (0,08 m)to / 4 = 5,03 x 10-3 mto
Kraften blir umiddelbart funnet gjennom F = m.g = 90.000 kg x 9.8 m / sto= 882.000 N.
Til slutt beregnes gjennomsnittlig innsats slik:
E = F / A = 882 000 N / 5,03 x 10-3 mto = 1,75 x 108 Pa = 175 MPa
Nå brukes ligningen for stress, vel vitende om at materialet har en elastisk respons:
E = Y. (δ / L)
Youngs modul av stål finnes i tabell 1:
δ = E.L / Y = 6 m x 1,75 x 108 Pa / 200 x 10 9 Pa = 5,25 x 10 -3 m = 5,25 mm.
Ingen har kommentert denne artikkelen ennå.