
Bevaring av det lineære momentum-prinsippet, eksempler, øvelser.
De bevaring av lineær fart av et legeme fastslår at produktet av massen og hastighetsvektoren er en konstant størrelse når kroppen er fri for interaksjon med andre legemer og med hastigheten målt i forhold til en fast eller ikke-akselerert referanseramme.
Når du har flere kropper som bare samhandler med hverandre, men ikke med det ytre miljøet, da lineær fart av settet forblir også konstant over tid.

Det lineære momentum, momentum eller bare momentum, er betegnet med brevet s y er en vektormengde:
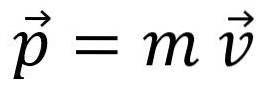
Momentum er ikke det samme som hastighet, selv om forholdet er åpenbart: for eksempel har en lastebil som går 20 km / t mer fart enn en sykkel som beveger seg i samme hastighet.
For at kroppens lineære momentum skal endres, må en netto ytre kraft virke inn på den, ellers forblir den konstant. Også det lineære øyeblikket P av et system dannet av n-kropper er vektorsummen av de enkelte øyeblikkene:
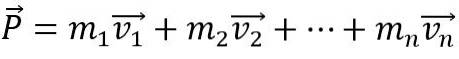
Artikkelindeks
- 1 Prinsipp for bevaring av lineær momentum
- 2 Eksempler
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 2.3 Eksempel 3
- 3 applikasjoner
- 3.1 Send i rommet
- 3.2 Dagligliv
- 4 Øvelser
- 4.1 Øvelse 1
- 4.2 Øvelse 2
- 5 Referanser
Prinsipp for bevaring av lineær momentum
I et kraftfritt legeme (eller en der alle kreftene på den avbrytes) skjer det at det lineære øyeblikket forblir konstant.
Det samme skjer i et system dannet av flere legemer som bare samhandler med hverandre, men ikke med det ytre miljøet: Systemets totale lineære momentum forblir fast under utviklingen av helhetens bevegelse..
Dette bevaringsprinsippet er angitt som følger:
Det totale momentet til et sett med n-kropper som bare samhandler med hverandre, men ikke med det ytre miljøet, er en uforanderlig mengde i tid.
Og matematisk uttrykkes det som følger:
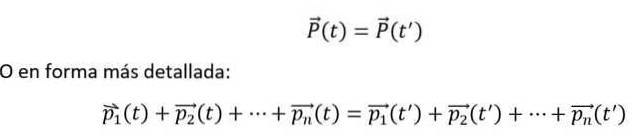
Ovennevnte likheter er oppfylt, hvis og bare hvis n-kroppene samhandler med hverandre, men ikke med det ytre miljøet. Videre må individuelle øyeblikk alltid måles i forhold til en treghetsreferanseramme..
Eksempler
Eksempel 1

To astronauter i rommet holder hender og holdes i en fast posisjon i forhold til romfartøyet. Men hvis de skyver hverandre, begynner de å skille seg i motsatt retning, sett fra skipet..
I dette tilfellet, ettersom samspillet mellom astronautene bare er mellom dem gjennom kontakten til hendene, er det totale momentumet etter skyving fortsatt den opprinnelige verdien i forhold til romfartøyet. Det vil si total momentum 0.
Imidlertid endret fremdriften til hver astronaut. Opprinnelig hadde hver et 0 lineært øyeblikk med hensyn til skipet, men etter å ha blitt presset, kommer en ut i den ene retningen og den andre i motsatt retning, med ikke-null lineære øyeblikk av samme størrelse og motsatt retning..
Når de individuelle momentene tilsettes vektorielt, oppnås således den totale totale momentum som et resultat, som er null.
På den annen side indikerer bevaring av momentummengden at astronauten med lavest masse er den som beveger seg raskere i forhold til romfartøyet. Men resultatet av å multiplisere massen med hastigheten er lik produktet oppnådd ved å multiplisere massen til den andre med hastigheten til den andre.
Eksempel 2
En valp er på en flytende plattform i en rolig innsjø, og eieren hans ser på ham fra en dokke. I begynnelsen er både plattformen og valpen i ro, men når valpen vil komme nærmere eieren, beveger plattformen seg bort fra kaien.
Forklaringen på denne observasjonen er nettopp i prinsippet om bevaring av mengden lineær momentum. Systemet består av valpen og plattformen.
Valpen kan gå på plattformen takket være friksjonskraften mellom bena og overflaten, i dette tilfellet er friksjonskraften en intern interaksjonskraft mellom den og plattformen.
Det hele er et isolert system, siden plattformen kan bevege seg horisontalt over innsjøen, uten motstand mot bevegelse. På den annen side, i vertikal retning er alle kreftene balansert og kompensert, og helheten har ingen bevegelse i den retningen..
Derfor oppfylles alle hypotesene i denne situasjonen slik at prinsippet om bevaring av lineær momentum gjelder.
Eksempel 3

En eskimo er fanget i midten av en frossen innsjø, isen er så glatt at uansett hvor hardt han prøver seg, glir eskimo og forblir alltid på samme sted.
Den eneste mulige måten for eskimoene å komme seg ut av innsjøen er at han kaster i motsatt retning som han vil flytte en tung gjenstand som han bærer i ryggsekken (forutsatt at han har en).
applikasjoner
Send i verdensrommet

Bevaring av lineær momentum påføres for å drive en rakett ut i verdensrommet der det ikke er noen eksterne krefter. I dette tilfellet oppnås impulsen til skipet ved å drive ut gasser med høy hastighet, slik at raketten kan bevege seg i motsatt retning som de ble kastet ut mot..
Hvis skipet opprinnelig er i ro, når det brenner og driver ut drivstoff, skjer utvisningskraften mot selve skipet. Det er en indre kraft mellom gassene og skipet. Det er ingen eksterne krefter, og derfor gjelder bevaring av lineær momentum.
Ettersom det lineære momentet til gassene er det samme og motsatt av skipets, klarer det å komme ut av hvile, og ved å fortsette å utdrive gasser øker det bevegelsesmengden og dermed hastigheten.
Dagliglivet

Et annet tilfelle av anvendelse av bevaring av lineær fart i hverdagen er å stikke en spiker i treet, og dra nytte av hammerens bevegelse eller fart..
Det kan hevdes at i dette tilfellet ikke prinsippet gjelder, fordi det er en ekstern kraft: motstanden som treet gir til neglen..
I kontaktøyeblikket er imidlertid kraften som hammeren påfører neglen, en indre kraft (mellom systemet som er neglen og hammeren) mye større enn motstanden som treet motarbeider, og derfor er sistnevnte ubetydelig.
Hele impulsen til hammeren, som er ganske stor på grunn av sin store masse og hastighet, overføres til neglen like etter kollisjonen. Legg merke til at hele øyeblikket, men ikke all kinetisk energi til hammeren, overføres, siden en del av dette blir transformert til termisk energi i neglen og i hammeren, noe som øker temperaturen etter støtet.
Opplæring
Øvelse 1
Astronautene Andrew og Berenice er utenfor romstasjonen og holder begge hender og i ro i forhold til stasjonen. De drives frem ved å skyve hendene på den ene mot den andre, og de blir løslatt. Hvis Andrew, 70 kg masse, beveger seg med 1 m / s i forhold til stasjonen, hva er hastigheten til Berenice med 49 kg masse?
Løsning
I dette tilfellet gjelder hypotesene om bevaring av lineær momentum tydelig, siden det ikke er noen eksterne krefter i verdensrommet. Kraften som begge astronauter skyver hendene med, er en intern styrke.
Anta at Andrews masse er Mtil og Berenice Mb. Tilsvarende er hastighetene til begge etter impulsen Vtil for Andrew og Vb for Berenice. Da gjelder bevaring av lineær momentum slik:
Mtil∙0 + Mb∙0 = Mtil∙Vtil+ Mb∙Vb
Å løse Berenices hastighet har vi:
Vb = - (Mtil / Mb) ∙ Vtil
Plassere de numeriske verdiene:
Vb = - (70/49) ∙ (1m / s) eller = -1,43m / s eller
Det vil si at Berenice beveger seg med en hastighet på 1,43 m / s i motsatt retning av Andrew.
Øvelse 2

En valp med en masse på 5 kg er i ro på en 15 kg plattform som flyter, også i ro, på en stille innsjø. Hvis valpen begynner å gå på plattformen med en hastighet på 0,5 m / s i forhold til den. Hvor raskt vil valpen og plattformen ha med hensyn til en observatør festet til bakken??
Løsning
Treghetsreferansesystemet blir tatt som kaien der eieren av valpen er. I utgangspunktet hviler både valpen og den flytende plattformen i forhold til kaien..
Når valpen bestemmer seg for å gå mot eieren raskt v ' i forhold til plattformen, så beveger plattformen seg vekk fra brygga med hastighet +V. Valpens hastighet i forhold til våren oppnås ved hjelp av vektorsummen av hastigheten i forhold til plattformen pluss hastigheten på plattformen, og vi betegner den med:
v = -v' + V
Ettersom vannets motstand mot plattformens bevegelse praktisk talt er null på grunn av dens lave hastighet, kan det oppgis at systemet består av valpen + plattformen er et isolert system og prinsippet om bevaring av lineær momentum gjelder:
0 = m ∙ v + M ∙ V
Husker at v = v '+ V vi har:
0 = -m ∙ v '+ m ∙ v + M ∙ V
Det vil si: m ∙ v '= (m + M) ∙ V
Derfor V = [m / (m + M)] v 'og v = - (M / m) V = - [M / (m + M)] v'
Erstatter de numeriske verdiene vi har:
V = [5 / (5 +15)] ∙ 0,5 m / s = 0,125 m / s
Dette er hastigheten som plattformen beveger seg vekk fra kaien.
V = - (15/20) ∙ 0,5m / s = -0,375 m / s
Og dette er hastigheten hvalpen nærmer seg kaien på.
Referanser
- Duke University. Systemer av partikler. Gjenopprettet fra: webhome.phy.duke.edu.
- Rex, A. 2011. Fundamentals of Physics. Pearson.
- Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 1. Pearson.
- Serway, R., Jewett, J. (2008). Fysikk for naturvitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning.
- .

Welcome to the world of adult Dating loveawake.ru