De absolutte konstanter er de konstantene som alltid opprettholder verdien under en beregningsprosess. Alle absolutte konstanter er numeriske verdier, og i noen tilfeller er de representert med bokstaver som utgjør det greske alfabetet.
Konseptet med konstant størrelse refererer til en hvis verdi forblir fast; Dette betyr at verdien ikke varierer og alltid forblir den samme. Denne verdien endres ikke så lenge situasjonen eller prosessen som størrelsen blir brukt på varer.
Artikkelindeks
Konstanter er absolutte fordi verdien deres aldri endres når en beregningsprosedyre utføres. Disse er også kjent som numeriske konstanter fordi de, som navnet antyder, er verdier representert av tall og i noen tilfeller med bokstaver, for eksempel:
- I ligningen: y = 4x + 1, er de absolutte konstantene 4 og 1.
Det er mange områder der absolutte konstanter implementeres; for eksempel i områder som fysikk, kjemi og matematikk, er bruken av dem veldig viktig fordi de hjelper til med å løse uendelig mange problemer.
Det er mange verdier av konstanter som fungerer som en referanse i de forskjellige alternativene for å løse øvelser; Absolutte konstanter som areal og volum er en av de mest brukte innen fagområder som ingeniørfag.
I dette området er det flere tall som representerer absolutte konstanter, som historisk har hjulpet i løsningen av mange problemer som har hjulpet i utviklingen av menneskeheten..
En av konstantene som har vært veldig relevant er pi (π), som har blitt studert siden antikken (1800 f.Kr.).
Mange århundrer senere var det Archimedes som bestemte verdien, som er et irrasjonelt tall som gjenspeiler forholdet mellom lengden på en omkrets og dens diameter..
Dette er beregnet ut fra forskjellige tilnærminger, den numeriske verdien er: 3.1415926535 ... og den består av omtrent 5000 * 109 desimaler.
Fra den konstante π var det mulig å utlede geometri området og volumet av koniske seksjoner og legemer i revolusjon, slik som sirkelen, sylinderen, kjeglen, sfæren, blant andre. Den brukes også til å uttrykke ligninger i radianer.
En annen veldig viktig konstant som brukes eller finnes i forskjellige områder er det gyldne tallet (φ), også kalt det gyldne tallet eller det gyldne middelverdiet. Det er et forhold eller proporsjon mellom to segmenter av en linje, uttrykt ved ligningen:
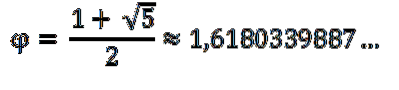
Det ble oppdaget i eldgamle tider og studert av Euklid. Dette forholdet er ikke bare representert i geometriske figurer som femkanter, men også i naturen, for eksempel i skallet på en snegl, i skjell, i frøene til solsikker og i bladene. Det kan også bli funnet i menneskekroppen.
Dette forholdet er kjent som guddommelig proporsjon, fordi det tillegger ting en estetisk karakter. På grunn av dette har den blitt brukt i arkitektonisk design, og forskjellige kunstnere som Leonardo Da Vinci har implementert den for sine verk..
Andre absolutte konstanter som er allment anerkjent og av like stor betydning er:
- Pythagoras konstant: √2 = 1.41421 ...
- Eulers konstant: γ = 0,57721 ...
- Naturlig logaritme: e = 2.71828 ...
I fysikk er en absolutt konstant den størrelsen hvis verdi, uttrykt i et enhetssystem, forblir uendret i fysiske prosesser over tid..
De er kjent som universelle konstanter fordi de har vært grunnleggende for studiet av forskjellige prosesser som spenner fra de enkleste til de mest komplekse fenomenene. Blant de mest kjente er:
Verdien er omtrent 299792458 m* s-1. Den brukes til å definere lengdenheten som lyset beveger seg i løpet av et år, og ut fra dette blir måling av lengdemåler født, noe som har vært viktig for målesystemer.
Dette bestemmer intensiteten til tyngdekraften mellom kroppene. Det er en del av studiene av Newton og Einstein, og dens omtrentlige verdi er 6,6742 (10) * 10-elleve N*mto/ kgto.
Denne konstanten er lik 8.854187817 ... * 10-12 F.*m-1.
Som er lik 1,25566370 * 10-6 N.TIL-to.
I kjemi, som i andre områder, er en absolutt konstant at data, prinsipp eller faktum som ikke er gjenstand for endringer eller variasjoner; refererer til kroppens konstanter eller til et sett med tegn som tillater oss å skille en kjemisk art fra en annen, for eksempel molekylvekten og atomvekten til hvert element.
Blant de viktigste absolutte kjemiske konstantene er:
Det er en av de viktigste konstantene. Med dette er det mulig å telle mikroskopiske partikler for å bestemme vekten av et atom; dermed etablerte forskeren Amedeo Avogadro at 1 mol = 6.022045 * 102. 3 muldvarp-1.
Lik 9, 10938 *10−31
Denne konstanten er lik 1,67262 *10−27
Tilsvarende 1,67492* 10−27
Tilsvarer 5,29177*10−11
Som er lik 2, 81794*10−15
Konstant som er lik 8.31451 (mto*kg) / (K* muldvarp* sto)
Den absolutte konstanten brukes også innen dataprogrammering, der den er definert som en verdi som ikke kan endres når et program blir utført; det vil si i dette tilfellet er det en fast lengde som er reservert fra datamaskinens minne.
I de forskjellige programmeringsspråkene blir konstantene uttrykt gjennom kommandoer.
- I C-språket blir absolutte konstanter erklært med kommandoen "#define". På den måten vil konstanten holde den samme verdien under utførelsen av et program..
For eksempel, for å indikere verdien av Pi (π) = 3.14159, skriver vi:
#inkludere
#definer PI 3.1415926
int main ()
printf ("Pi er verdt% f", PI);
retur 0;
- I både C ++ og Pascal-språk blir konstanter befalt med ordet "const".
Ingen har kommentert denne artikkelen ennå.