
Konstant av integrasjonsbetydning, beregning og eksempler

De konstant integrering Det er en merverdi for beregningen av antiderivativer eller integraler, den tjener til å representere løsningene som utgjør primitivet til en funksjon. Uttrykk en iboende tvetydighet der en hvilken som helst funksjon har et uendelig antall primitiver.
For eksempel hvis vi tar funksjonen: f (x) = 2x + 1 og vi får antiderivativ:
∫ (2x + 1) dx = xto + x + C ; Hvor C er den konstant integrering og representerer grafisk den vertikale oversettelsen mellom de uendelige mulighetene til primitivet. Det er riktig å si det (xto + x) er en av primitivene til f (x).
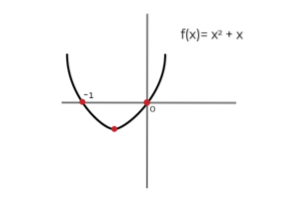
På samme måte kan vi definere en (xto + x + C ) som primitiv for f (x).
Artikkelindeks
- 1 Omvendt eiendom
- 2 Den ubestemte integralen
- 3 Andre betydninger av konstant integrasjon
- 4 Hvordan beregnes integrasjonskonstanten?
- 5 eksempler
- 5.1 Eksempel 1
- 5.2 Eksempel 2
- 5.3 Eksempel 3
- 6 Forslag til øvelser
- 6.1 Øvelse 1
- 6.2 Øvelse 2
- 6.3 Øvelse 3
- 6.4 Øvelse 4
- 7 Referanser
Omvendt eiendom
Det kan bemerkes at ved å avlede uttrykket (xto + x) funksjonen f (x) = 2x + 1 oppnås. Dette skyldes den omvendte egenskapen som eksisterer mellom avledning og integrering av funksjoner. Denne egenskapen gjør det mulig å få integrasjonsformler med utgangspunkt i differensieringen. Som tillater verifisering av integraler gjennom de samme derivatene.
Imidlertid (xto + x) er ikke den eneste funksjonen hvis derivat er lik (2x + 1).
- d (xto + x) / dx = 2x + 1
- d (xto + x + 1) / dx = 2x + 1
- d (xto + x + 2) / dx = 2x + 1
- d (xto + x + 3) / dx = 2x + 1
- d (xto + x + C) / dx = 2x + 1
Hvor 1, 2, 3 og 4 representerer bestemte primitiver av f (x) = 2x + 1. Mens 5 representerer den ubestemte eller primitive integralen av f (x) = 2x + 1.
Primitivene til en funksjon oppnås gjennom antiderivasjon eller integrert prosess. Hvor F vil være en primitiv av f hvis følgende er sant
- y = ∫ f (x) dx = F (x) + C; C = konstant integrering
- F '(x) = f (x)
Det kan sees at en funksjon har et enkelt derivat, i motsetning til dets uendelige primitiver som følge av integrasjon.
Den ubestemte integralen
∫ f (x) dx = F (x) + C
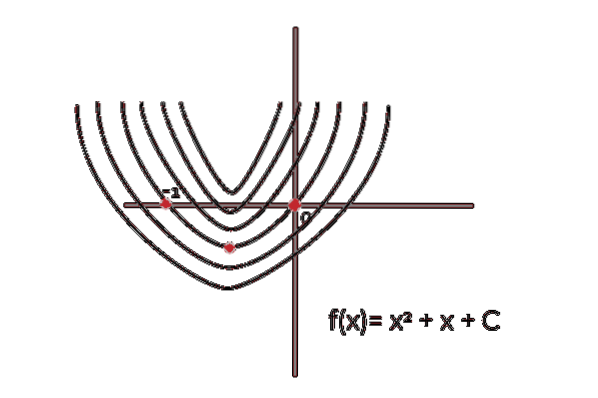
Det tilsvarer en familie av kurver med samme mønster, som opplever uoverensstemmelse i verdien av bildene til hvert punkt (x, y). Hver funksjon som oppfyller dette mønsteret vil være en individuell primitiv og settet med alle funksjoner er kjent som ubestemt integral.
Verdien av konstant integrering vil være den som skiller hver funksjon i praksis.
De konstant integrering antyder et vertikalt skifte i alle grafer som representerer primitivene til en funksjon. Hvor parallelliteten mellom dem blir observert, og det faktum at C er verdien av forskyvningen.
I henhold til vanlig praksis konstant integrering det er betegnet med bokstaven "C" etter et tillegg, selv om det i praksis ikke betyr noe om konstanten blir lagt til eller trukket fra. Dens virkelige verdi kan bli funnet på forskjellige måter i henhold til forskjellige Innledende forhold.
Andre betydninger av konstant integrasjon
Det ble allerede snakket om hvordan konstant integrering påføres i grenen av integrert kalkulator; Representerer en familie av kurver som definerer den ubestemte integralen. Men mange andre vitenskaper og grener har tildelt veldig interessante og praktiske verdier av konstant integrering, som har lagt til rette for utvikling av flere studier.
I fysisk konstanten av integrasjon kan ta flere verdier avhengig av dataenes art. Et veldig vanlig eksempel er å kjenne til funksjonen V (t) som representerer hastighet av en partikkel versus tid t. Det er kjent at når en primitiv av V (t) beregnes, oppnås funksjonen R (t) som representerer posisjon partikkel versus tid.
De konstant integrering vil representere verdien av utgangsposisjonen, det vil si på tidspunktet t = 0.
Tilsvarende, hvis funksjonen er kjent A (t) som representerer akselerasjon av partikkelen versus tid. Primitivet til A (t) vil resultere i funksjonen V (t), der konstant integrering vil være verdien av starthastigheten V.0.
I økonomi, ved å oppnå ved hjelp av integrasjon en primitiv funksjon for en kostnadsfunksjon. De konstant integrering vil representere faste kostnader. Og så mange andre applikasjoner som fortjener differensial- og integralkalkulus.
Hvordan beregnes integrasjonskonstanten?
For å beregne konstant integrering, det vil alltid være nødvendig å kjenne til Innledende forhold. Hvilke er ansvarlige for å definere hvilke av de mulige primitivene som tilsvarer.
I mange applikasjoner blir det behandlet som en uavhengig variabel på tidspunktet (t), hvor konstanten C tar verdiene som definerer Innledende forhold av den spesielle saken.
Hvis vi tar det første eksemplet: ∫ (2x + 1) dx = xto + x + C
En gyldig startbetingelse kan være å forutsette at grafen går gjennom en bestemt koordinat. For eksempel er det kjent at den primitive (xto + x + C) passerer gjennom punktet (1, 2)
F (x) = xto + x + C; dette er den generelle løsningen
F (1) = 2
Vi erstatter den generelle løsningen i denne likheten
F (1) = (1)to + (1) + C = 2
Fra hvor det lett følger det C = 0
På denne måten er den tilsvarende primitive for denne saken F (x) = xto + x
Det er flere typer numeriske øvelser som fungerer med konstanter av integrasjon. Faktisk slutter ikke differensial- og integralregningen å bli brukt i nåværende undersøkelser. På forskjellige faglige nivåer finnes de; fra innledende beregning, gjennom blant annet fysikk, kjemi, biologi, økonomi.
Det sees også i studien av differensiallikninger, hvor i konstant integrering Det kan ta forskjellige verdier og løsninger, dette på grunn av flere avledninger og integrasjoner som utføres i denne saken.
Eksempler
Eksempel 1
- En 30 meter høy kanon skyter et prosjektil vertikalt oppover. Starthastigheten til prosjektilet er kjent for å være 25 m / s. Bestemme seg for:
- Funksjonen som definerer posisjonen til prosjektilet med hensyn til tid.
- Flytidspunktet eller tidspunktet da partikkelen treffer bakken.
Det er kjent at i en jevnt variert rettlinjet bevegelse er akselerasjonen en konstant verdi. Dette er tilfellet med prosjektilskytingen, hvor akselerasjonen vil være tyngdekraften
g = - 10 m / sto
Det er også kjent at akselerasjonen er det andre derivatet av posisjonen, noe som indikerer en dobbel integrasjon i oppløsningen til øvelsen, og dermed oppnår to konstanter av integrasjon.
A (t) = -10
V (t) = ∫A (t) dt = ∫ (-10t) dt = -10t + C1
Oppgavens første forhold indikerer at starthastigheten er V0 = 25 m / s. Dette er hastigheten på tidspunktet t = 0. På denne måten er det tilfreds med at:
V (0) = 25 = -10 (0) + C1 Y C1 = 25
Hastighetsfunksjonen blir definert
V (t) = -10t + 25; Likheten med MRUV-formelen (VF = V0 + a x t)
På en homolog måte fortsetter vi med å integrere hastighetsfunksjonen for å oppnå uttrykket som definerer posisjonen:
R (t) = ∫V (t) dt = ∫ (-10t + 25) dt = -5tto + 25t + Cto
R (t) = -5tto + 25t + Cto (primitiv av posisjon)
Utgangsposisjonen R (0) = 30 m er kjent. Deretter beregnes den spesielle primitive av prosjektilet.
R (0) = 30m = -5 (0)to + 25 (0) + Cto . Hvor Cto = 30
Den første delen er løst siden R (t) = -5tto + 25t + 30 ; Dette uttrykket er homologt med forskyvningsformelen i MRUV R (t) = R0 + V0t - gtto/to
For den andre delen må den kvadratiske ligningen løses: -5tto + 25t + 30 = 0
Siden dette betinger partikkelen å nå bakken (posisjon = 0)
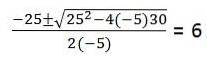
Faktisk gir 2. grads ligning oss to løsninger T: 6, -1. Verdien t = -1 ignoreres fordi det er tidsenheter hvis domene ikke inkluderer negative tall.
På denne måten løses den andre delen der flytiden er lik 6 sekunder.
Eksempel 2
- Finn den primitive f (x) som tilfredsstiller de opprinnelige betingelsene:
- f "(x) = 4; f '(2) = 2; f (0) = 7
Med informasjonen til det andre derivatet f "(x) = 4 begynner antiderivasjonsprosessen
f '(x) = ∫f "(x) dx
∫4 dx = 4x + C1
Deretter kjenner vi tilstanden f '(2) = 2, og fortsetter:
4 (2) + C1 = 2
C1 = -6 og f '(x) = 4x - 8
Fortsett på samme måte for det andre konstant integrering
f (x) = ∫f '(x) dx
∫ (4x - 8) dx = 2xto - 8x + Cto
Starttilstanden f (0) = 7 er kjent, og vi fortsetter:
2 (0)to - 8 (0) + Cto = 7
Cto = 7 og f (x) = 2xto - 8x + 7
- f "(x) = xto ; f '(0) = 6; f (0) = 3
På en lignende måte som forrige problem definerer vi de første derivatene og den opprinnelige funksjonen fra de opprinnelige forholdene.
f '(x) = ∫f "(x) dx
∫ (xto) dx = (x3/ 3) + C1
Med tilstanden f '(0) = 6 fortsetter vi:
(03/ 3) + C1 = 6; Hvor1 = 6 og f '(x) = (x3/ 3) + 6
Så den andre konstant integrering
f (x) = ∫f '(x) dx
∫ [(x3/ 3) + 6] dx = (x4/ 12) + 6x + Cto
Starttilstanden f (0) = 3 er kjent, og vi fortsetter:
[(0)4/ 12] + 6 (0) + Cto = 3; Hvorto = 3
Dermed får vi den primitive spesifikasjonen
f (x) = (x4/ 12) + 6x + 3
Eksempel 3
- Definer de primitive funksjonene gitt derivatene og et punkt på grafen:
- dy / dx = 2x - 2 som passerer gjennom punktet (3, 2)
Det er viktig å huske at derivater refererer til hellingen til linjen som tangerer kurven på et gitt punkt. Der det ikke er riktig å anta at grafen til derivatet berører det angitte punktet, siden dette tilhører grafen til den primitive funksjonen.
På denne måten uttrykker vi differensiallikningen som følger:
dy = (2x - 2) dx ; så når vi bruker anti-derivasjonskriteriene har vi:
∫dy = ∫ (2x - 2) dx
y = xto - 2x + C
Bruke den opprinnelige tilstanden:
2 = (3)to - 2 (3) + C
C = -1
Er oppnådd: f (x) = xto - 2x - 1
- dy / dx = 3xto - 1 Hva passerer gjennom punktet (0, 2)
Vi uttrykker differensiallikningen som følger:
dy = (3xto - 1) dx ; så når vi bruker anti-derivasjonskriteriene har vi:
Dy = ∫ (3xto - 1) dx
y = x3 - x + C
Bruke starttilstanden:
2 = (0)to - 2 (0) + C
C = 2
Er oppnådd: f (x) = x3 - x + 2
Foreslåtte øvelser
Øvelse 1
- Finn den primitive f (x) som tilfredsstiller de opprinnelige betingelsene:
- f "(x) = x; f '(3) = 1; f (2) = 5
- f "(x) = x + 1; f '(2) = 2; f (0) = 1
- f "(x) = 1; f '(2) = 3; f (1) = 10
- f "(x) = -x; f '(5) = 1; f (1) = -8
Øvelse 2
- En ballong som stiger med en hastighet på 16 ft / s, faller en pose med sand fra en høyde på 64 ft over bakkenivå.
- Definer flytiden
- Hva vil vektoren VF når jeg treffer gulvet?
Øvelse 3
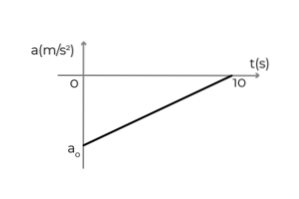
- Figuren viser akselerasjonstidsgrafen til en bil som beveger seg i positiv retning av x-aksen. Bilen kjørte med en konstant hastighet på 54 km / t da føreren trakk bremsene for å stoppe på 10 sekunder. Fastslå:
- Den første akselerasjonen av bilen
- Hastigheten på bilen ved t = 5s
- Forskyvningen av bilen under oppbremsing
Øvelse 4
- Definer de primitive funksjonene gitt derivatene og et punkt på grafen:
- dy / dx = x som passerer gjennom punktet (-1, 4)
- dy / dx = -xto + 1 Hva passerer gjennom punktet (0, 0)
- dy / dx = -x + 1 som går gjennom punktet (-2, 2)
Referanser
- Integrert kalkulator. Den ubestemte integral- og integrasjonsmetoden. Wilson, Velásquez Bastidas. Magdalena University 2014
- Stewart, J. (2001). Beregning av en variabel. Tidlige transcendentals. Mexico: Thomson Learning.
- Jiménez, R. (2011). Matematikk VI. Integrert kalkulator. Mexico: Pearson Education.
- Fysikk I. Mc Graw hill



Ingen har kommentert denne artikkelen ennå.