
Kvadrilaterale elementer, egenskaper, klassifisering, eksempler
EN firkant er en polygon med fire sider og fire hjørner. Deres motsatte sider er de som ikke har felles hjørner, mens de er påfølgende sider de med et felles toppunkt.
I en firkant er de tilstøtende vinkler de som deler en side, mens motsatte vinkler de har ingen sider til felles. En annen viktig egenskap ved en firkant er at summen av dens fire indre vinkler er to ganger planvinkelen, det vil si 360 ° eller 2π radianer.
Diagonaler er segmentene som forbinder et toppunkt med det motsatte og i en gitt firkant, fra hver toppunkt kan en enkelt diagonal tegnes. Totalt antall diagonaler i en firkant er to.
Kvadrilaterale figurer er kjent for menneskeheten siden antikken. De arkeologiske opptegnelsene, samt konstruksjonene som overlever i dag, vitner om dette..
Likeledes fortsetter firsidene i dag å ha en viktig tilstedeværelse i alles hverdag. Leseren kan finne dette skjemaet på skjermen der teksten blir lest akkurat nå, på vinduer, dører, bildeler og utallige andre steder..
Artikkelindeks
- 1 Klassifisering av firkant
- 1.1 Typer parallellogram
- 2 Trapes
- 2.1 Typer trapeser
- 3 Parallelogram
- 3.1 Område av et parallellogram
- 3.2 Diagonaler av et parallellogram
- 3.3 Parallellogramloven
- 4 rektangel
- 4.1 Diagonaler av et rektangel
- 5 kvadrat
- 6 Rhombus
- 7 Eksempler
- 7.1 Eksempel 1
- 7.2 Eksempel 2
- 7.3 Eksempel 3
- 8 Øvelser løst
- 8.1 - Øvelse 1
- 8.2 - Øvelse 2
- 9 Referanser
Quadrilateral klassifisering
I henhold til parallelliteten til de motsatte sidene, er firsidene klassifisert som følger:
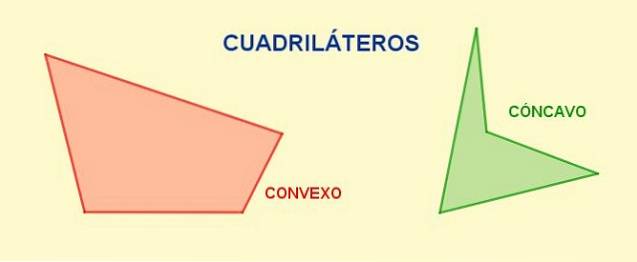
- Trapes, når det ikke er noen parallellitet og firsiden er konveks.
- Trapes, når det er parallellitet mellom et enkelt par motsatte sider.
- Parallelogram, når de motsatte sidene er parallelle to og to.
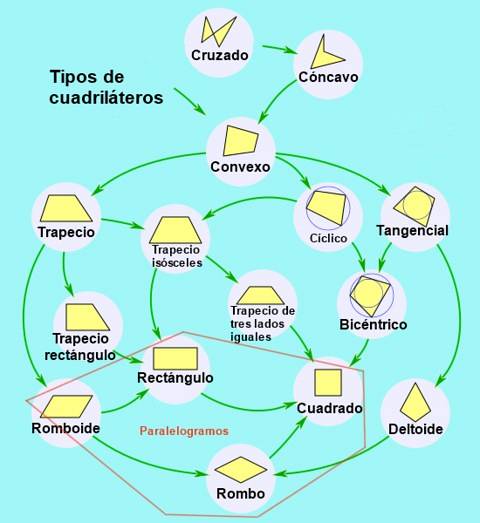
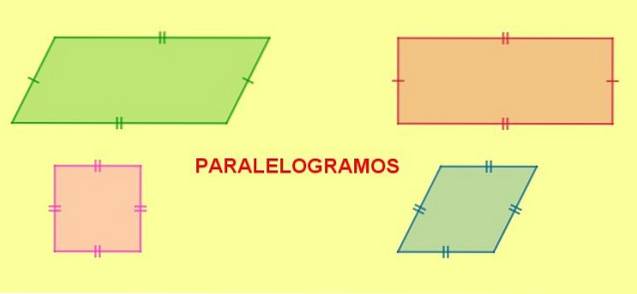
Typer parallellogram
I sin tur kan parallellogrammer klassifiseres i henhold til deres vinkler og sider som følger:
- Rektangel, er parallellogrammet som har sine fire indre vinkler med like mål. De indre vinklene til et rektangel danner en rett vinkel (90º).
- Torget, er et rektangel med sine fire sider av like mål.
- Diamant, er parallellogrammet med sine fire like sider, men forskjellige tilstøtende vinkler.
- Rhomboid, parallellogram med forskjellige tilstøtende vinkler.
Trapes
Trapesformet er en konveks firkant med to parallelle sider.
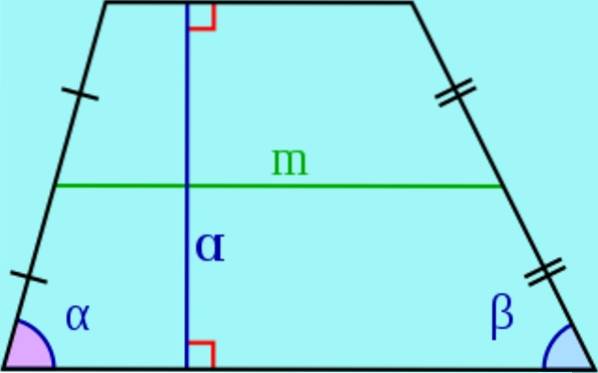
- I en trapesform kalles de parallelle sidene baser og ikke-parallellene kalles lateral.
- De høyde av en trapes er avstanden mellom de to basene, det vil si lengden på et segment med ender ved basene og vinkelrett på dem. Dette segmentet kalles også en høyde på trapesen..
- De median er segmentet som slutter seg til midtpunktene til sidene. Det kan vises at medianen er parallell med trapesformens baser, og lengden er lik halvsummen av basene.
- Området til en trapes er høyden multiplisert med halvsummen av basene:
Areal til en trapesform = høyde * (base 1 + base 2) / 2
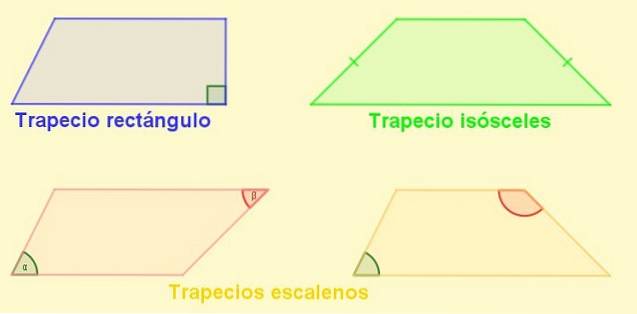
Typer trapeser
-Rektangel trapesformet: Er den med en lateral vinkelrett på basene. Denne laterale er også høyden på trapeset.
-Trapes likbenet: Den med sider av like lengde. I en likeben trapes er vinklene like ved basene like.
-Scalene trapes: Den med sidene i forskjellige lengder. Dens motsatte vinkler kan være den ene akutte og den andre stumpe, men det kan også hende at begge er stumpe eller begge er akutte..
Parallelogram
Parallellogrammet er et firkant som har motsatte sider parallelt to og to. I et parallellogram er de motsatte vinklene like og de tilstøtende vinklene er supplerende, eller med andre ord, de tilstøtende vinklene legger opp til 180º.
Hvis et parallellogram har en rett vinkel, vil alle andre vinkler være det også, og den resulterende figuren kalles rektangel. Men hvis rektangelet også har tilstøtende sider av samme lengde, er alle sidene like og den resulterende figuren er a torget.
Når et parallellogram har to tilstøtende sider av samme lengde, vil alle sidene ha samme lengde, og den resulterende figuren er a diamant.
Høyden på et parallellogram er et segment med ender på motsatte sider og vinkelrett på dem..
Område av et parallellogram
Arealet til et parallellogram er produktet av basen ganger høyden, og basen er en side vinkelrett på høyden (figur 6).
Areal av et parallellogram = base x høyde = a. h
Diagonaler av et parallellogram
Kvadratet av diagonalen som starter fra et toppunkt er lik summen av kvadratene til de to sidene ved siden av toppunktet pluss dobbeltproduktet fra disse sidene ved cosinus for vinkelen til toppunktet:
Fto = ato + dto + 2 a d Cos (α)
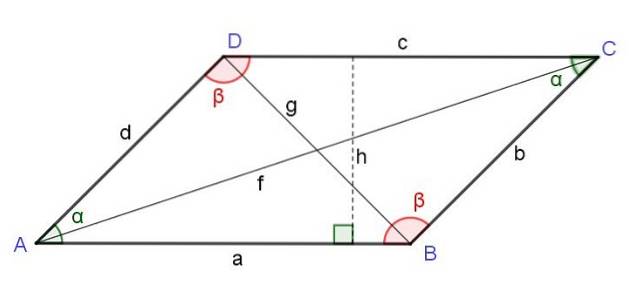
Kvadratet av diagonalen motsatt toppunktet til et parallellogram er lik summen av kvadratene til de to sidene ved siden av toppunktet og trekker dobbeltproduktet fra disse sidene ved cosinus av vinkelen til toppunktet:
gto = ato + dto - 2 a d Cos (α)
Loven om parallellogrammer
I ethvert parallellogram er summen av kvadratene på sidene lik summen av kvadratene til diagonalene:
tilto + bto + cto + dto = fto + gto
Reflette
Rektangelet er en firkant med sine motsatte sider parallelle to og to, og som også har en rett vinkel. Rektangelet er med andre ord en type parallellogram med rett vinkel. For å være parallellogram, rektangelet har motsatte sider av samme lengde a = c og b = d.
Men som i ethvert parallellogram er de tilstøtende vinklene supplerende og motsatte vinkler like, i rektangelet fordi det har en rett vinkel, vil det nødvendigvis danne rette vinkler i de andre tre vinklene. Nemlig i et rektangel måler alle innvendige vinkler 90º eller π / 2 radianer.
Diagonaler av et rektangel
I et rektangel er diagonalene like lange, som vist nedenfor. Begrunnelsen er som følger; Et rektangel er et parallellogram med alle dets rette vinkler og arver derfor alle egenskapene til parallellogrammet, inkludert formelen som gir lengden på diagonalene:
Fto = ato+ dto + 2 a d Cos (α)
gto = ato + dto - 2 a d Cos (α)
med α = 90º
Hva Cos (90º) = 0, så skjer det at:
Fto = gto = ato + dto
Det er f = g, og derfor lengdene F Y g av de to diagonalene i rektangelet er like og lengden er gitt av:
Diagonaler lengde på et rektangel = √ (ato + bto)
Også, hvis i et rektangel med tilstøtende sider til Y b den ene siden tas som basen, den andre siden vil være i høyden og følgelig vil arealet til rektangelet være:
Areal av rektangelet = a x b.
Omkretsen er summen av alle sidene av rektangelet, men siden motsetningene er like, følger det at for et rektangel med sider til Y b omkretsen er gitt med følgende formel:
Rektangelets omkrets = 2 (a + b)
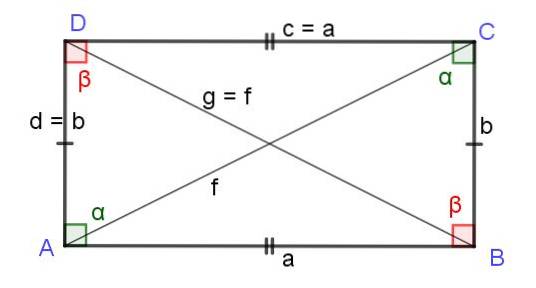
Torget
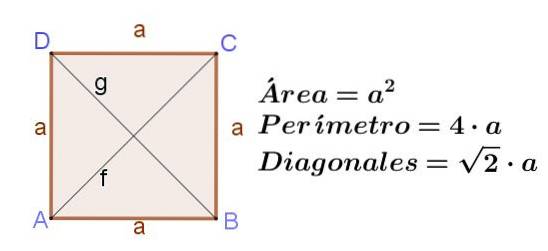
Firkanten er et rektangel med tilstøtende sider av samme lengde. Hvis torget har en side til, deretter diagonalene F Y g har samme lengde, som er f = g = (√2) a.
Området til et kvadrat er dets kvadrat:
Område av et kvadrat = ato
Omkretsen til et kvadrat er to ganger siden:
Omkrets av et kvadrat = 4 a
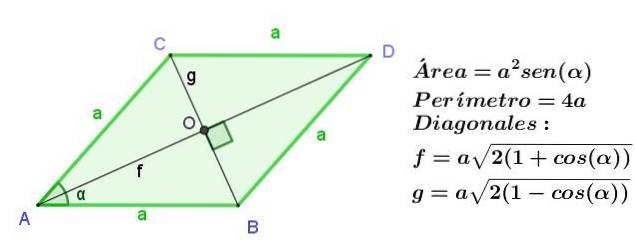
Diamant
Romben er et parallellogram med tilstøtende sider av samme lengde, men som i et parallellogram er de motsatte sidene like da, alle sider av en rombe er like lange.
Diagonalene til en rombe er av ulik lengde, men skjæres i rette vinkler.
Eksempler
Eksempel 1
Vis at de indre vinklene i en firkant (ikke krysset) til sammen 360 °.
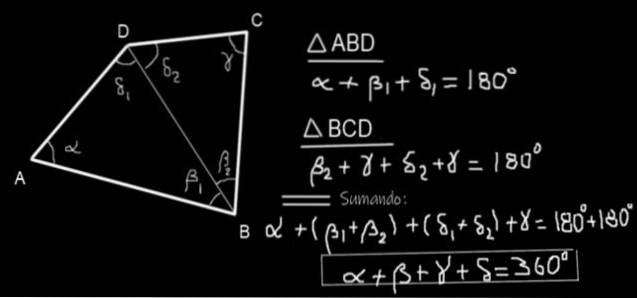
En firkantet ABCD vurderes (se figur 10) og den diagonale BD er tegnet. To trekanter ABD og BCD dannes. Summen av de innvendige vinklene til trekanten ABD er:
α + β1 + δ1 = 180º
Og summen av de indre vinklene til trekanten BCD er:
β2 + γ + δto = 180º
Legge til de to ligningene vi får:
α + β1 + δ1 + βto + γ + δto = 180º + 180º
Gruppering:
α + (β1 + βto) + (δ1 + δto) + γ = 2 * 180 °
Ved å gruppere og gi nytt navn, vises det endelig at:
α + β + δ + γ = 360º
Eksempel 2
Vis at medianen til en trapes er parallell med basene, og lengden er halvsummen av basene.
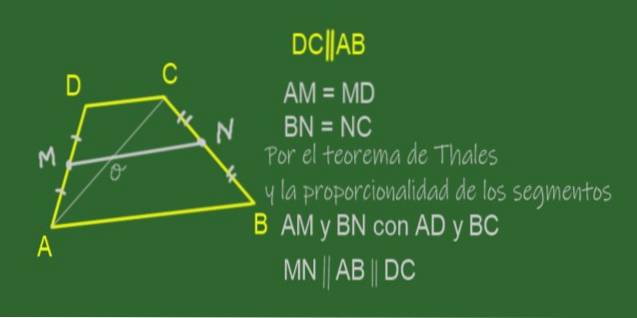
Medianen til en trapes er segmentet som forbinder midtpunktene på sidene, det vil si de ikke-parallelle sidene. I trapesformet ABCD vist i figur 11 er medianen MN.
Siden M er midtpunktet til AD og N er midtpunktet for BC, er det sant at forholdene AM / AD og BN / BC er like.
Det vil si at AM er proporsjonal med BN i samme andel som AD er mot BC, så vilkårene er gitt for anvendelse av Thales (gjensidige) setning som sier følgende:
"Hvis proporsjonale segmenter bestemmes i tre eller flere linjer kuttet av to sekanter, så er disse linjene parallelle".
I vårt tilfelle konkluderes det at linjene MN, AB og DC er parallelle med hverandre, derfor:
"Lmedianen til en trapes er parallell med basene".
Nå skal Thales-setningen brukes:
"Et sett med paralleller kuttet av to eller flere sekanter bestemmer proporsjonale segmenter".
I vårt tilfelle AD = 2 AM, AC = 2 AO, så er trekanten DAC lik trekanten MAO, og følgelig DC = 2 MO.
Et lignende argument lar oss bekrefte at CAB ligner CON, hvor CA = 2 CO og CB = 2 CN. Det følger umiddelbart at AB = 2 PÅ.
Kort sagt, AB = 2 ON og DC = 2 MO. Så når vi legger til har vi:
AB + DC = 2 PÅ + 2 MO = 2 (MO + PÅ) = 2 MN
Endelig er MN ryddet:
MN = (AB + DC) / 2
Og det konkluderes med at medianen til en trapes måler halvsummen av basene, eller med andre ord: medianen måler summen av basene, delt på to.
Eksempel 3
Vis at diagonalene i en rombe krysser vinkelrett.

Tavlen i figur 12 viser nødvendig konstruksjon. Først tegnes parallellogrammet ABCD med AB = BC, det vil si en rombe. Diagonaler AC og DB bestemmer åtte vinkler som er vist på figuren.
Ved bruk av teoremet (a.i.p.) som sier at alternative indre vinkler mellom paralleller kuttet av en sekant bestemmer like vinkler, kan vi etablere følgende:
α1 = γ1, α2 = γ2, δ1 = Β1 og δ2 = β2. (*)
På den annen side, siden de tilstøtende sidene av en rombe er like lange, bestemmes fire likestilte trekanter:
DAB, BCD, CDA og ABC
Nå påberopes trekanten (likebenede) setning, som sier at vinklene ved siden av basen er like store, og det konkluderes med at:
δ1 = β2, δ2 = β1, α2 = γ1 og α1 = γ2 (**)
Hvis relasjonene (*) og (**) kombineres, oppnås følgende vinkellikhet:
α1 = α2 = γ1 = γ1 på den ene siden og β1 = Β2 = δ1 = δ2 på den andre.
Når vi husker de like trekantsetningen som sier at to trekanter med en lik side mellom to like vinkler er like, har vi:
AOD = AOB og følgelig også vinklene ∡AOD = ∡AOB.
Da ∡AOD + ∡AOB = 180º, men siden begge vinklene er like store, har vi 2 ∡AOD = 180º som betyr at ∡AOD = 90º.
Det vil si at det er vist geometrisk at diagonalene til en rombe krysser vinkelrett.
Øvelser løst
- Øvelse 1
Vis at de ikke-rette vinklene er supplerende i riktig trapesform.
Løsning
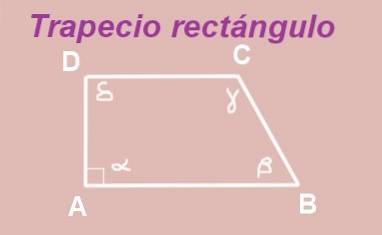
Trapesformet ABCD er konstruert med baser AB og DC parallelle. Innvendige vinkelen til toppunkt A er riktig (den måler 90º), så vi har en rett trapes.
Vinkler α og δ er indre vinkler mellom to paralleller AB og DC, derfor er de like, det vil si δ = α = 90º.
På den annen side har det blitt vist at summen av de indre vinklene til en firkant legger opp til 360 °, det vil si:
α + β + γ + δ = 90º + β + 90º + δ = 360º.
Ovennevnte fører til:
β + δ = 180º
Bekrefte hva som ønsket å vise, at vinklene β og δ er supplerende.
- Øvelse 2
Et parallellogram ABCD har AB = 2 cm og AD = 1 cm, i tillegg er vinkelen BAD 30º. Bestem arealet til nevnte parallellogram og lengden på de to diagonalene.
Løsning
Arealet til et parallellogram er produktet av lengden på basen ganger høyden. I dette tilfellet blir lengden på segmentet b = AB = 2 cm lagt til grunn, den andre siden har lengden a = AD = 1 cm og høyden h vil bli beregnet som følger:
h = AD * Sen (30º) = 1 cm * (1/2) = ½ cm.
Så: Areal = b * h = 2 cm * ½ cm = 1 cmto.
Referanser
- C. E. A. (2003). Element av geometri: med øvelser og geometri av kompasset. University of Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematikk 2. Grupo Editorial Patria.
- Freed, K. (2007). Oppdag polygoner. Referanseutdanningsfirma.
- Hendrik, V. (2013). Generelle polygoner. Birkhäuser.
- IGER. (s.f.). Matematikk Første semester Tacaná. IGER.
- Jr. geometri. (2014). Polygoner. Lulu Press, Inc..
- Miller, Heeren & Hornsby. (2006). Mathematics: Reasoning And Applications (Tiende utgave). Pearson Education.
- Patiño, M. (2006). Matematikk 5. Redaksjonell Progreso.
- Wikipedia. Quadrilaterals. Gjenopprettet fra: es.wikipedia.com



Ingen har kommentert denne artikkelen ennå.