
Derivat av kotangentberegning, bevis, øvelser
De derivat av cotangenten er lik det motsatte av kvadratet til cosecanten "-Cscto”. Denne formelen overholder lovene til derivater per definisjon og differensiering av trigonometriske funksjoner. Det er betegnet som følger:
d (ctg u) = -cscto eller. du
Hvor "du" symboliserer uttrykket avledet fra argumentfunksjonen, med hensyn til den uavhengige variabelen.

Artikkelindeks
- 1 Hvordan beregnes det?
- 2 Kjennetegn på cotangentfunksjonen
- 2.1 Vertikale asymptoter
- 2.2 Domene
- 2.3 Rekkevidde
- 2.4 Frekvens
- 2.5 Atferd
- 3 Demo
- 3.1 Trigonometrisk differensisikker
- 3.2 Bevis per definisjon av derivat
- 4 Løst øvelser
- 4.1 Øvelse 1
- 4.2 Øvelse 2
- 5 Referanser
Hvordan beregnes det?
Fremgangsmåten for å utvikle disse derivatene er ganske enkel. Alt du trenger å gjøre er å identifisere argumentet riktig og hvilken type funksjon det representerer..
For eksempel har uttrykket Ctg (f / g) en inndeling i argumentet. Dette vil kreve en differensiering av U / V etter utvikling av derivatet av cotangenten.
Cotangenten er den gjensidige av tangenten. Algebraisk betyr dette at:
(1 / tg x) = ctg x
Ctg x = Cos x / Sen x
Det er feil å si at cotangensfunksjonen er den "inverse" av tangenten. Dette er fordi den omvendte tangensfunksjonen per definisjon er buetangens.
(Tg-1 x) = arctg x
I følge Pythagoras trigonometri er cotangenten involvert i følgende seksjoner:
Ctg x = (cos x) / (sin x)
Ctgto x + 1 = Cscto x
I følge analytisk trigonometri reagerer den på følgende identiteter:
Ctg (a + b) = (1 - tg a. Tg b) / (tg a + tg b)
Ctg (a - b) = (1 + tg a. Tg b) / (tg a - tg b)
Ctg (2a) = (1 - tgto a) / (2tg a)
Kjennetegn på cotangentfunksjonen
Det er nødvendig å analysere forskjellige egenskaper ved funksjonen f (x) = ctg x for å definere de aspektene som er nødvendige for å studere dens differensialitet og anvendelse.
Vertikale asymptoter
Cotangent-funksjonen er ikke definert på verdiene som gjør uttrykket "Senx" null. På grunn av dets ekvivalente Ctg x = (cos x) / (sin x), vil den ha en ubestemmelighet i alle "nπ" med n som tilhører heltallene.
Det vil si at i hver av disse verdiene på x = nπ vil det være en vertikal asymptote. Når du nærmer deg fra venstre vil verdien av cotangenten synke raskt, og når du nærmer deg fra høyre, vil funksjonen øke på ubestemt tid.
Domene
Domenet til cotangentfunksjonen uttrykkes med settet x ∈ R / x ≠ nπ, n ∈ Z. Dette leses som "x tilhører settet med reelle tall slik at x er forskjellig fra nπ, med n tilhører settet med heltall".
Rang
Området for cotangentfunksjonen er fra minus til pluss uendelig. Derfor kan det konkluderes med at rekkevidden er settet med reelle tall R.
Frekvens
Den cotangente funksjonen er periodisk og perioden er lik π. På denne måten oppfylles likheten Ctg x = Ctg (x + nπ), hvor n tilhører Z.
Oppførsel
Det er en merkelig funksjon, siden Ctg (-x) = - Ctg x. På denne måten er det kjent at funksjonen presenterer en symmetri med hensyn til koordinatopprinnelsen. Det presenterer også en reduksjon i hvert intervall som ligger mellom to påfølgende vertikale asymptoter.
Den har ikke maksimums- eller minimumsverdier, fordi dens tilnærminger til de vertikale asymptotene viser atferd der funksjonen øker eller avtar på ubestemt tid.
Nullene eller røttene til cotangentfunksjonen er funnet med oddetallene av π / 2. Dette betyr at Ctg x = 0 holder for verdier av formen x = nπ / 2 med n oddetall.
Demonstrasjon
Det er to måter å bevise derivatet av cotangent-funksjonen.
Trigonometrisk differensial
Derivatet av cotangensfunksjonen fra dets ekvivalente i sinus og cosinus er bevist.
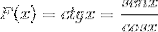
Det blir behandlet som avledet av en funksjonsdeling
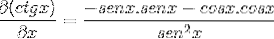
Etter å ha utledet er faktorene gruppert, og målet er å etterligne de pythagoreiske identitetene
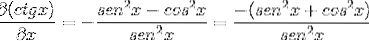
Ved å erstatte identitetene og bruke gjensidighet oppnås uttrykket
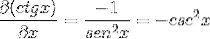
Bevis per definisjon av derivat
Følgende uttrykk tilsvarer derivatet per definisjon. Der avstanden mellom 2 punkter i funksjonen nærmer seg null.
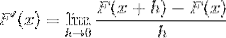
Erstatter for cotangenten vi har:
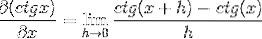
Identiteter brukes for summen av argumenter og gjensidighet
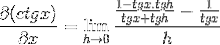
Brøken av telleren brukes tradisjonelt
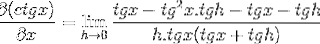
Å eliminere de motsatte elementene og ta en felles faktor, får vi
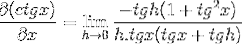
Å bruke Pythagoras identiteter og gjensidighet må vi
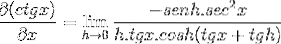
Elementene evaluert i x er konstante med hensyn til grensen, derfor kan de legge igjen argumentasjonen for dette. Da blir egenskapene til trigonometriske grenser brukt.
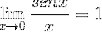
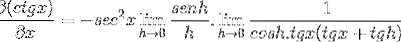
Grensen vurderes
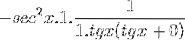
Deretter faktureres den til ønsket verdi er nådd
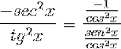
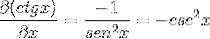
Derivatet av cotangenten demonstreres således som det motsatte av kvadratet til cosecanten.
Løst øvelser
Øvelse 1
Basert på funksjonen f (x), definer uttrykket f '(x)
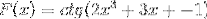
Den tilsvarende avledningen brukes med respekt for kjederegelen
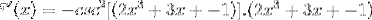
Henter argumentet
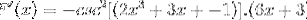
Noen ganger er det nødvendig å bruke gjensidige eller trigonometriske identiteter for å tilpasse løsningene.
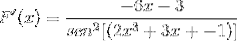
Øvelse 2
Definer differensialuttrykket som tilsvarer F (x)
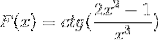
I henhold til avledningsformelen og med respekt for kjederegelen
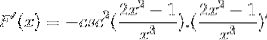
Argumentet er avledet, mens resten forblir den samme
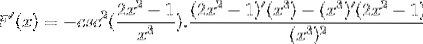
Henter alle elementene
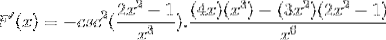
Opererer på en tradisjonell måte produktene fra samme base
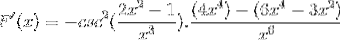
De like elementene tilsettes og den felles faktoren ekstraheres
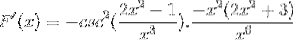
Skilt er forenklet og betjent. Gi vei til fullt avledet uttrykk
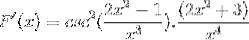
Referanser
- Trigonometrisk serie, bind 1. A. Zygmund. Cambridge University Press, 2002
- Beregning av en enkelt variabel. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. nov 2008
- Kalkulus med trigonometri og analytisk geometri. John H. Saxon, John Saxon, Frank Wang, Diana Harvey. Saxon Publishers, 1988
- Multivariabel analyse. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. des. 2010
- Systemdynamikk: modellering, simulering og kontroll av mekatroniske systemer. Dekan C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. mars 2012
- Kalkulus: Matematikk og modellering. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1. jan 1999



Ingen har kommentert denne artikkelen ennå.