
Implisitte derivater hvordan de løses og øvelser løses
De implisitte derivater De er verktøy som brukes i en differensieringsteknikk som brukes på funksjoner. De brukes når det ikke er mulig, under vanlige metoder, å fjerne den avhengige variabelen som skal utledes. Denne klareringen utføres basert på den uavhengige variabelen.
For eksempel i uttrykket 3xy3 - 2y + xyto = xy, du kan ikke få uttrykket som definerer “y” som en funksjon av “x”. Slik at ved å utlede differensialuttrykket kan dy / dx oppnås.

Artikkelindeks
- 1 Hvordan løses implisitte derivater??
- 2 Kjederegel
- 3 Driftsordre
- 4 Implisitt av en funksjon
- 5 Historie
- 6 Søknader
- 7 Løst øvelser
- 7.1 Øvelse 1
- 7.2 Øvelse 2
- 8 Referanser
Hvordan løses implisitte derivater?
For å løse et implisitt derivat starter vi med et implisitt uttrykk. For eksempel: 3xy3 - 2y + xyto - xy = 0. Dette er allerede løst riktig, men å gjøre det er ikke en nødvendig forutsetning for å oppnå derivatet av y med hensyn til x. Deretter blir hvert av elementene avledet med respekt for kjederegelen for blandede funksjoner:
3xy3 består av to variabler, derfor er d (3xy3) vil bli behandlet som avledet av et produkt av funksjoner.
d (3xy3) / dx = 3 år3 + 3 årto.(3x) y '= 3 år3 + 9xyto Y '
Der elementet y 'er kjent som “og fetter”Y representerer dy / dx
-2y Det er avledet i henhold til loven K.U = K.U '
d (-2y) = -2 y '
xyto antar en annen differensial sammensatt av et produkt av funksjoner
d (xyto) = ogto + 2xy og '
-x og behandles homologt
d (-xy) = -y - x y '
De er erstattet i likhet, vel vitende om at derivatet av null er null.
3 år3 + 9xyto y '- 2 y' + yto + 2xy y '- y - x y' = 0
Elementene som har begrepet y 'er gruppert på den ene siden av likheten
3 år3 + Yto - y = -9xyto y '+ 2 y' + x y '
Den vanlige faktoren y 'trekkes ut på høyre side av likheten
3 år3 + Yto - y = y '(-9xyto + x + 2)
Til slutt blir begrepet som multipliserer y 'fjernet. Dermed får man uttrykket som tilsvarer det implisitte derivatet av y med hensyn til x.
y '= dy / dx = (3 år3 + Yto - y) / (- 9xyto + x + 2)
Kjederegel
Ved implisitt avledning respekteres alltid kjederegelen. Alle differensialuttrykk vil bli gitt som en funksjon av den uavhengige variabelen X. Så hver variabel θ annet enn X, må inkludere begrepet dθ / dx etter at den er avledet.
Dette begrepet vises bare i første grad eller med en eksponent lik 1. Denne egenskapen gjør det helt klart under tradisjonelle factoring-metoder. Dermed er det mulig å oppnå uttrykket som definerer differensialen dθ / dx.
Kjederegelen viser den progressive naturen til differensiering eller avledet prosess. Hvor for hver sammensatte funksjon f [g (x)], har vi at differensialuttrykket til f vil være
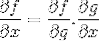
Driftsordre
I hver formel eller avledningslov som blir brukt, må rekkefølgen av variablene innbyrdes tas i betraktning. Kriteriene knyttet til den uavhengige variabelen respekteres, uten å endre korrelasjonen med den avhengige variabelen..
Forholdet mellom den avhengige variabelen på tidspunktet for avledning blir tatt direkte; med unntak av at dette vil bli betraktet som en andre funksjon, og det er derfor kjederegelkriteriet brukes for blandede funksjoner.
Dette kan utvikles i uttrykk med mer enn 2 variabler. Under de samme prinsippene vil alle differensialene som refererer til de avhengige variablene bli betegnet.
Grafisk håndteres det samme kriteriet som definerer derivatet. Mens derivatet er helling av tangentlinjen til kurven i planet, representerer resten av differensialene som hører til de avhengige variablene (dy / dx, dz / dx) plan som er tangent til vektorlegemene beskrevet av de flere variable funksjonene.
Implisitt av en funksjon
En funksjon sies å være implisitt definert, dersom uttrykket y = f (x) kan representeres som en multiplokal variabel funksjon F (x, y) = 0 så lenge F er definert i R-planetto.
3xy3 - 2y + xyto = xy kan skrives i form 3xy3 - 2y + xyto - xy = 0
Med tanke på umuligheten av å gjøre eksplisitt funksjonen y = f (x).
Historie
Differensialregningen begynte å bli navngitt av forskjellige matematiske forskere rundt det syttende århundre. Første gang det ble nevnt var gjennom bidrag fra Newton og Leibniz. Begge behandlet differensialregningen fra forskjellige synsvinkler, men konvergerte i resultatene.
Mens Newton fokuserte på differensiering som en hastighet eller endringshastighet, var Leibniz tilnærming mer geometrisk. Det kan sies at Newton angrep formodningene som Apollonius av Perge og Leibniz etterlot de geometriske ideene til Fermat..
Den implisitte avledningen vises umiddelbart når man vurderer differensial- og integralligninger. Disse utvidet Leibniz geometriske konsept til R3 og til og med flerdimensjonale rom.
applikasjoner
Implisitte derivater brukes i forskjellige situasjoner. De er vanlige i valutakursproblemer mellom relaterte variabler, hvor variablene, avhengig av følelsen av studien, vil bli ansett som avhengige eller uavhengige..
De har også interessante geometriske applikasjoner, for eksempel i refleksjon eller skyggeproblemer, på figurer hvis form kan matematisk modelleres..
De brukes ofte innen økonomi og prosjektering, samt i ulike undersøkelser av naturfenomener og eksperimentelle bygninger..
Løst øvelser
Øvelse 1
Definer det implisitte uttrykket som definerer dy / dx
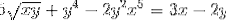
Hvert element i uttrykket er differensiert
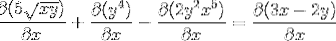
Å etablere kjederegelen i hvert kompetent tilfelle
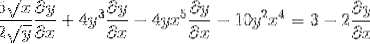
Gruppere elementene som har dy / dx på den ene siden av likhet
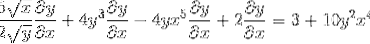
Det er fakturert ved hjelp av den vanlige faktoren
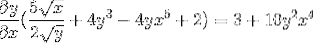
Det er løst å oppnå ønsket uttrykk
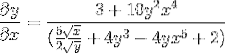
Øvelse 2
Definer det implisitte uttrykket som definerer dy / dx
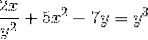
Å uttrykke derivatene som skal utføres
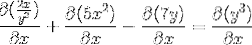
Deriverer implisitt i henhold til kjedelegelen
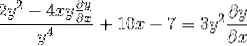
Faktorering av vanlige elementer
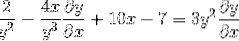
Gruppere begrepet dy / dx på den ene siden av likestillingen
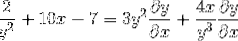
Felles faktor for differensialelementet
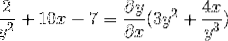
Vi isolerer og oppnår ønsket uttrykk
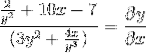
Referanser
- Beregning av en enkelt variabel. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. nov 2008
- The Implicit Function Theorem: History, Theory, and Applications. Steven G. Krantz, Harold R. Parks. Springer Science & Business Media, 9. nov. 2012
- Multivariabel analyse. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. des. 2010
- Systemdynamikk: modellering, simulering og kontroll av mekatroniske systemer. Dekan C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. mars 2012
- Kalkulus: Matematikk og modellering. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1. jan 1999


Ingen har kommentert denne artikkelen ennå.