Dynamikk i et system med partikler eksempler, øvelser

De dynamikken i et partikelsystem Den består av anvendelse av Newtons bevegelseslover på et sett med partikler, som kan være diskrete (partiklene kan telles) eller utgjøre en del av et utvidet objekt, i dette tilfellet er systemet kontinuerlig.

For å forklare bevegelsen til et system av partikler er det upraktisk å analysere hver enkelt separat og se hvilke krefter som virker på det. I stedet defineres et representativt punkt for settet, kalt Massesenter.

Å beskrive bevegelsen til massesenteret gir en veldig nøyaktig oversikt over helhetens samlede bevegelse, det gjør det også mulig å bruke Newtons lover på en måte som er analog med når objektet blir ansett som en dimensjonsfri partikkel.

Denne siste modellen, kalt partikkelmodell, Det er bra for å beskrive oversettelser og også når du ikke trenger å vurdere dimensjonene til objektet. Men vanlige gjenstander har størrelse, og hvis de også har rotasjonsbevegelse, er det nødvendig å ta hensyn til punktene som kreftene påføres.

Artikkelindeks

• 1 Eksempler
  • 1.1 Jorden og månen
  • 1.2 Utvidede objekter
• 2 Massesenteret til et system av partikler
  • 2.1 CM bevegelse
  • 2.2 Kraft på CM
• 3 Øvelsen løst
  • 3.1 Løsning a
  • 3.2 Løsning b
  • 3.3 Løsning c
• 4 Referanser

Eksempler

Jorden og månen

Et sett med diskrete partikler m₁, m_to, m₃... som til slutt beveger seg med hensyn til opprinnelsen til et koordinatsystem, på grunn av en eller annen resulterende kraft som virker på dem, er et godt eksempel på et partikelsystem.

Jorden kan betraktes som en partikkel og månen en annen, da utgjør begge et system med to partikler under påvirkning av solens tyngdekraft..

Utvidede objekter

En person, et dyr eller et hvilket som helst objekt i miljøet kan også betraktes som et partikelsystem, bare at disse er så små at de ikke kan telles en etter en. Dette er et kontinuerlig system, men når man tar hensyn til visse hensyn, er behandlingen det samme som for et diskret system.

Nedenfor er detaljene.

Massesenteret til et system av partikler

For å begynne studiet av et partikelsystem, må vi finne massesenteret (CM), som er det punktet der hele massen i systemet er konsentrert..

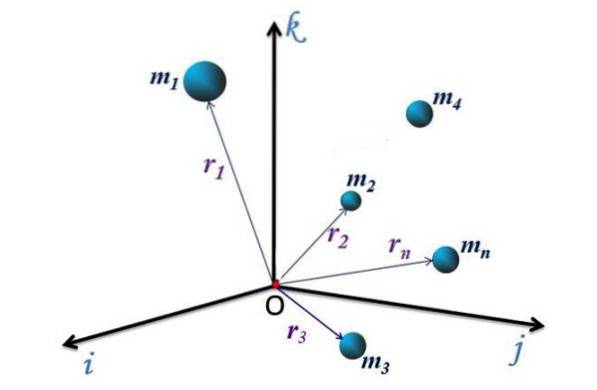
For det diskrete systemet i figur 1, med n partikler, har hver en posisjonsvektor rettet fra opprinnelsen O til koordinatsystemet til punktet P (x, y, z) hvor partikkelen er. Disse vektorene er betegnet som r₁, r_to, r₃... r_n.

Koordinatene til CM beregnes ved hjelp av følgende ligninger:

Hvor hver av massene i settet er representert som m₁, m_to, m₃... m_n. Merk at summeringen ∑ m_Jeg tilsvarer den totale massen M av enheten. Hvis systemet er kontinuerlig, erstattes summasjonene med integraler.

Hver av de vinkelrette retningene er representert av enhetsvektorene Jeg, j Y k, derav posisjonsvektoren til CM, betegnet r_CM, kan uttrykkes av:

r_CM = x_CM Jeg + Y_CM j + z_CM k

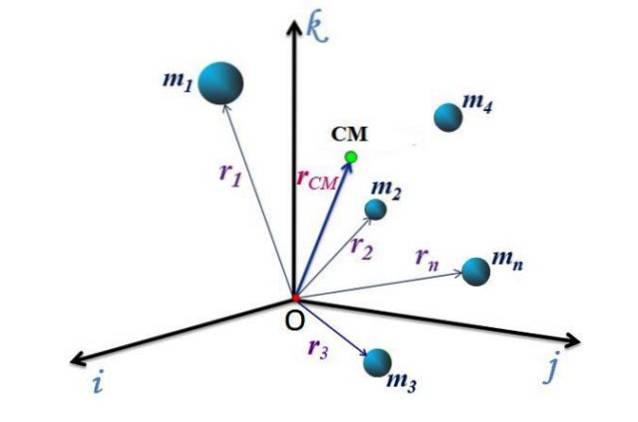
CM bevegelse

Når plasseringen av massesenteret er kjent, gjelder de kjente ligningene. Hastigheten til CM er det første derivatet av posisjonen med hensyn til tid:

I dette tilfellet har systemet total fart P som beregnes som produktet av systemets totale masse og hastigheten til massesenteret:

P = M ∙v_CM

Alternativt kan systemets totale momentum beregnes direkte:

P = m₁v₁ + m_tov_to + m₃v₃ +…. = ∑ m_Jeg v_Jeg

Mens akselerasjonen til CM er avledet av hastigheten:

Tving på CM

Kreftene som virker på et system av partikler kan være:

• Interne krefter på grunn av samspill mellom de samme partiklene.
• Eksterne krefter, forårsaket av agenter utenfor systemet.

Ettersom de indre kreftene presenteres i par, av samme størrelse og retning, men motsatt retning, ifølge Newtons tredje lov, er det sant at:

∑ F_int = 0

Derfor endrer ikke de indre kreftene bevegelsen til helheten, men de er veldig viktige for å bestemme den indre energien..

Hvis systemet er isolert og det ikke er noen eksterne krefter, er massesenteret ifølge Newtons første lov i ro eller beveger seg med jevn rettlinjet bevegelse. Ellers opplever massesenteret en akselerasjon gitt av:

∑ F_ekst = M ∙til_CM

Hvor M er systemets totale masse. Ovennevnte ligning kan skrives slik:

Og det betyr at den ytre kraften tilsvarer den tidsmessige variasjonen i momentum, en annen måte å uttrykke Newtons andre lov og den samme som den berømte engelske fysikeren brukte i sin bok Prinsipp.

Treningen løst

Massesenteret til et 2-partikelsystem er på x-aksen i et bestemt øyeblikk, i posisjonen x = 2,0 m og beveger seg med hastighet 5,0 m / s i samme retning og i positiv retning. Hvis en av partiklene har opprinnelse, og den andre med en vekt på 0,1 kg, er i ro på x = 8,0 m, beregner du:

a) Massen av partikkelen som er ved opprinnelsen.

b) Mengden bevegelse av systemet

c) Hva er hastigheten på partikkelen ved opprinnelsen?

Løsning til

Fra ligningen for posisjonen til massesenteret:

r_CM = x_CM Jeg + Y_CM j + z_CM k = 2,0 m Jeg

Siden CM bare har en x-koordinat, brukes bare den første ligningen av trioen som er gitt tidligere:

Nå er koordinatene erstattet, hvis partikkelen ved opprinnelsen er betegnet som nummer 1 og den andre som nummer 2, er de numeriske dataene:

x₁ = 0 m, x_to = 8,0 m, m_to = 0,1 kg, x_CM = 2,0 m

Gjenstående:

Løsning b

Mengden bevegelse av systemet beregnes av:

P = M ∙v_CM

Den totale massen M er lik:

M = 0,3 kg + 0,1 kg = 0,4 kg

Derfor:

P = 0,4 kg ∙ 5,0 m / s Jeg = 2 kg.m / s Jeg

Løsning c

Fra ligningen for P av et to-partikkel system, tømmer det v₁, siden de andre dataene er kjent, siden uttalelsen sier at partikkel 2 er i ro, derfor:

v_to = 0 

Y P det ser ganske enkelt ut som:

P = m₁v₁

v₁ = P / m₁ = 2 kg.m / s Jeg / 0,3 kg = 6,67 m / s Jeg

Referanser

1. Duke University. Systemer av partikler. Gjenopprettet fra: webhome.phy.duke.edu.
2. Rex, A. 2011. Fundamentals of Physics. Pearson.
3. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 1. Pearson.
4. Serway, R., Jewett, J. (2008). Fysikk for naturvitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning.
5. Tipler, P. (2006) Fysikk for vitenskap og teknologi. 5. utg. Bind 1. Redaksjonell Reverté.