De Euklidisk avstand er et positivt tall som indikerer skillet mellom to punkter i et rom der aksiomene og setningene til Euklids geometri er oppfylt.
Avstanden mellom to punkter A og B i et euklidisk rom er lengden på vektoren AB tilhører den eneste linjen som går gjennom disse punktene.
Rommet vi oppfatter og hvor vi mennesker beveger oss, er et tredimensjonalt rom (3-D), der aksiomene og teoremene til Euklids geometri blir oppfylt. To-dimensjonale delområder (plan) og endimensjonale delområder (linjer) er inneholdt i dette rommet..
Euklidiske mellomrom kan være endimensjonale (1-D), to-dimensjonale (2-D), tredimensjonale (3-D) eller n-dimensjonale (n-D).
Poeng i det endimensjonale rommet X er de som hører til den orienterte linjen (OX), retningen fra O til X er den positive retningen. For å finne punktene på denne linjen brukes det kartesiske systemet, som består i å tildele hvert punkt på linjen et tall.
Artikkelindeks
Den euklidiske avstanden d (A, B) mellom punktene A og B, plassert på en linje, er definert som kvadratroten til firkanten av forskjellene i deres X-koordinater:
d (A, B) = √ ((XB - XA) ^ 2)
Denne definisjonen garanterer at: avstanden mellom to punkter alltid er en positiv mengde. Og at avstanden mellom A og B er lik avstanden mellom B og A..
Figur 1 viser det endimensjonale euklidiske rommet dannet av linjen (OX) og flere punkter på linjen. Hvert punkt har en koordinat:
Punkt A har koordinat XA = 2,5, punkt B koordinat XB = 4 og punkt C koordinat XC = -2,5
d (A, B) = √ ((4 - 2,5) 2) = 1,5
d (B, A) = √ ((2,5 - 4) 2) = 1,5
d (A, C) = √ ((- 2,5 - 2,5) 2) = 5,0
To-dimensjonalt euklidisk rom er et plan. Punktene til et euklidisk plan oppfyller aksiomene til Euklids geometri, for eksempel:
- En enkelt linje går gjennom to punkter.
- Tre punkter på planet danner en trekant hvis indre vinkler alltid legger opp til 180º.
- I en høyre trekant er firkantet av hypotenusen lik summen av kvadratene på bena.
I to dimensjoner har et punkt X- og Y-koordinater.
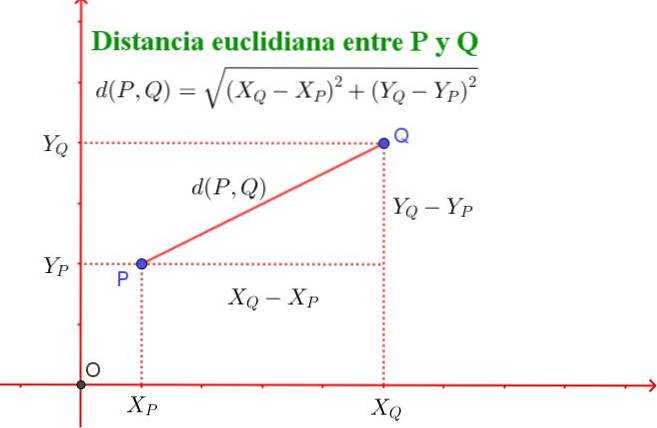
For eksempel har et punkt P koordinater (XP, YP) og et punkt Q-koordinater (XQ, YQ).
Den euklidiske avstanden mellom punkt P og Q er definert med følgende formel:
d (P, Q) = √ ((XQ - XP) ^ 2 + (YQ - YP) ^ 2)
Det skal bemerkes at denne formelen tilsvarer Pythagoras teorem, som vist i figur 2.
Ikke alle todimensjonale rom samsvarer med euklidisk geometri. Overflaten til en kule er et todimensjonalt rom.
Vinklene til en trekant på en sfærisk overflate blir ikke opptil 180º, og med dette oppfylles ikke det pythagoriske teoremet, og derfor oppfyller ikke en sfærisk overflate Euklids aksiomer.
Begrepet koordinater kan utvides til større dimensjoner:
- I 2-D punkt har P koordinater (XP, YP)
- I 3-D har et punkt Q koordinater (XQ, YQ, ZQ)
- I 4-D punkt vil R ha koordinater (XR, YR, ZR, WR)
- I n-D vil et punkt P ha koordinater (P1, P2, P3,…, Pn)
Avstanden mellom to punkter P og Q i et n-dimensjonalt euklidisk rom beregnes med følgende formel:
d (P, Q) = √ ((Q1 - P1) ^ 2 + (Q2 - P2) ^ 2 + ... + (Qn - Pn) ^ 2)
Stedet for alle punkter Q i et n-dimensjonalt euklidisk rom som er like langt fra et annet fast punkt P (sentrum), danner en n-dimensjonal hypersfære.
Det følgende viser hvordan avstanden mellom to punkter i det euklidiske tredimensjonale rommet beregnes.
Anta punkt A av kartesiske koordinater x, y, z gitt av A :( 2, 3, 1) og punkt B for koordinater B :( -3, 2, 2).
Vi vil bestemme avstanden mellom disse punktene, som det generelle forholdet brukes til:
d (A, B) = √ ((-3 - 2) 2 + (2-3) 2 + (2 - 1) 2) = √ ((-5) 2 + (-1) 2 + (1) 2 )
d (A, B) = √ (25 + 1 + 1) = √ (27) = √ (9 * 3) = 3 √ (3) = 5,196
Det er to punkter P og Q. Punktet P av kartesiske koordinater x, y, z gitt av P :( 2, 3, 1) og punktet Q for koordinatene Q :( -3, 2, 1).
Det blir bedt om å finne koordinatene til midtpunktet M i segmentet [PQ] som forbinder de to punktene.
Løsning:
Det ukjente punktet M antas å ha koordinater (X, Y, Z).
Siden M er midtpunktet til [PQ], må det være sant at d (P, M) = d (Q, M), så d (P, M) ^ 2 = d (Q, M) ^ 2 må også være sant :
(X - 2) ^ 2 + (Y - 3) ^ 2 + (Z - 1) ^ 2 = (X - (-3)) ^ 2 + (Y - 2) ^ 2 + (Z - 1) ^ 2
Som i dette tilfellet er den tredje sikt lik i begge medlemmer, forrige uttrykk forenkler til:
(X - 2) ^ 2 + (Y - 3) ^ 2 = (X + 3) ^ 2 + (Y - 2) ^ 2
Vi har da en ligning med to ukjente X og Y. Det kreves en annen ligning for å løse problemet.
Punkt M tilhører linjen som går gjennom punktene P og Q, som vi kan beregne som følger:
Først er regissørvektoren PQ av den rette: PQ = < -3-2, 2-3, 1-1> = < -5, -1, 0 >.
Seinere P.M. = OP + til PQ, hvor OP er posisjonsvektoren til punkt P og til er en parameter som hører til de reelle tallene.
Ovennevnte ligning er kjent som linjens vektorligning, som i kartesiske koordinater har følgende form:
< X-2, Y-3, Z-1> = <2, 3, 1> + til < -5, -1, 0> = < 2 - 5a, 3 - a, 0>
Likestiller de tilsvarende komponentene vi har:
X - 2 = 2-5 a; Y - 3 = 3 -a; Z - 1 = 0
Det vil si X = 4 - 5a, Y = 6 - a, til slutt Z = 1.
Det er erstattet i det kvadratiske uttrykket som relaterer X til Y:
(4 - 5a - 2) ^ 2 + (6 - a - 3) ^ 2 = (4 - 5a + 3) ^ 2 + (6 - a - 2) ^ 2
Det er forenklet:
(2 - 5a) ^ 2 + (3 -a) ^ 2 = (7 - 5a) ^ 2 + (4 - a) ^ 2
Utfolder seg nå:
4 + 25 a ^ 2 - 20a + 9 + a ^ 2 - 6a = 49 + 25 a ^ 2 - 70a + 16 + a ^ 2 - 8a
Det er forenklet og avbryter like vilkår i begge medlemmer:
4 - 20a + 9 - 6a = 49 - 70a + 16 - 8a
Parameteren a tømmes:
52 a = 49 + 16 - 4-9 = 52 som resulterer i at a = 1.
Det vil si X = 4-5, Y = 6-1, til slutt Z = 1.
Til slutt får vi de kartesiske koordinatene til midtpunktet M i segmentet [PQ]:
M: (-1, 5, 1).
Ingen har kommentert denne artikkelen ennå.