De Poisson-fordeling er en diskret sannsynlighetsfordeling, gjennom hvilken det er mulig å vite sannsynligheten for at innenfor en stor utvalgsstørrelse og i løpet av et bestemt intervall, en hendelse oppstår hvis sannsynligheten er liten.
Ofte kan Poisson-fordelingen brukes i stedet for binomialfordelingen, så lenge følgende betingelser er oppfylt: stort utvalg og liten sannsynlighet.
Siméon-Denis Poisson (1781-1840) opprettet denne distribusjonen som bærer navnet hans, veldig nyttig når det gjelder uforutsigbare hendelser. Poisson publiserte sine resultater i 1837, et forskningsarbeid om sannsynligheten for forekomst av feilaktige straffedommer.
Senere tilpasset andre forskere fordelingen i andre områder, for eksempel antall stjerner som kunne bli funnet i et visst romvolum, eller sannsynligheten for at en soldat døde av hestens spark..
Artikkelindeks
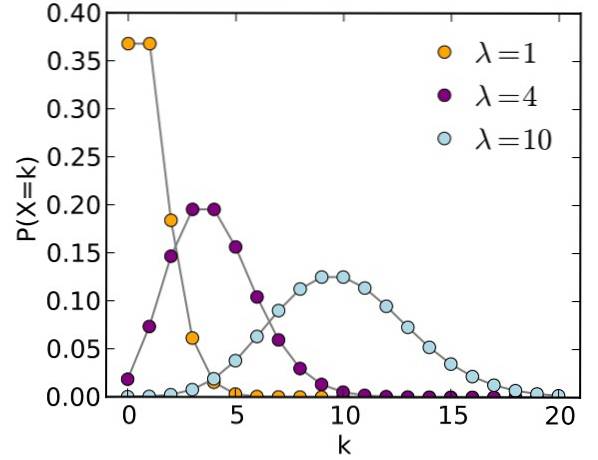
Den matematiske formen for Poisson-fordelingen er som følger:
- μ (også noen ganger betegnet som λ) er gjennomsnittet eller parameteren for fordelingen
- Euler nummer: e = 2,71828
- Sannsynligheten for å oppnå y = k er P
- k er antall suksesser 0, 1,2,3 ...
- n er antall tester eller hendelser (prøvestørrelsen)
Diskrete tilfeldige variabler, som navnet antyder, avhenger av tilfeldigheter og tar bare diskrete verdier: 0, 1, 2, 3, 4 ..., k.
Gjennomsnittet av fordelingen er gitt av:
Variansen σ, som måler spredningen av dataene, er en annen viktig parameter. For Poisson-distribusjonen er det:
σ = μ
Poisson bestemte at når n → ∞, og p → 0, ble gjennomsnittet μ -også kalt forventet verdi- har en tendens til en konstant:
μ → konstant
Viktig: s er sannsynligheten for at hendelsen skal forekomme med tanke på den totale befolkningen, mens P (y) er Poisson-spådommen på prøven.
Poisson-distribusjonen har følgende egenskaper:
-Prøvestørrelsen er stor: n → ∞.
-Hendelsene eller hendelsene som er vurdert er uavhengige av hverandre og skjer tilfeldig.
-Sannsynlighet P den bestemte hendelsen Y oppstår i løpet av en bestemt periode er veldig liten: P → 0.
-Sannsynligheten for at mer enn en hendelse inntreffer i tidsintervallet er 0.
-Gjennomsnittsverdien er tilnærmet en konstant gitt av: μ = n.p (n er prøvestørrelsen)
-Siden dispersjonen σ er lik μ, da den vedtar større verdier, blir variabiliteten også større.
-Hendelsene må fordeles jevnt i tidsintervallet som brukes.
-Settet med mulige hendelsesverdier Y er: 0,1,2,3,4 ... .
-Summen av Jeg variabler som følger en Poisson-fordeling, er også en annen Poisson-variabel. Gjennomsnittsverdien er summen av gjennomsnittsverdiene til disse variablene.
Poisson-fordelingen skiller seg fra binomialfordelingen på følgende viktige måter:
-Binomialfordelingen påvirkes av både prøvestørrelsen n og sannsynligheten P, men Poisson-fordelingen påvirkes bare av gjennomsnittet μ.
-I en binomial fordeling, de mulige verdiene til den tilfeldige variabelen Y er 0,1,2, ..., N, derimot i Poisson-fordelingen er det ingen øvre grense for disse verdiene.
Poisson brukte opprinnelig sin berømte distribusjon på rettssaker, men på industrielt nivå var en av hans tidligste bruksområder å lage øl. I denne prosessen brukes gjærkulturer til gjæring.
Gjær består av levende celler, hvis populasjon varierer over tid. Ved produksjon av øl er det nødvendig å tilsette den nødvendige mengden, derfor er det nødvendig å vite hvor mye celler det er per volumenhet.
Under andre verdenskrig ble Poisson-distribusjonen brukt til å finne ut om tyskerne faktisk siktet mot London fra Calais, eller bare skyte tilfeldig. Dette var viktig for de allierte for å avgjøre hvor god teknologien var tilgjengelig for nazistene..
Anvendelsene av Poisson-fordelingen refererer alltid til teller i tid eller teller i rommet. Og siden sannsynligheten for forekomst er liten, er den også kjent som "loven om sjeldne hendelser".
Her er en liste over hendelser som faller inn i en av disse kategoriene:
-Registrering av partiklene i et radioaktivt forfall, som som vekst av gjærceller, er en eksponentiell funksjon.
-Antall besøk på et bestemt nettsted.
-Ankomst av folk i kø for å betale eller delta (køteori).
-Antall biler som passerer et bestemt punkt på en vei i løpet av et gitt tidsintervall.
-Mutasjoner i en viss DNA-streng etter å ha mottatt strålingseksponering.
-Antall meteoritter med en diameter større enn 1 m falt i løpet av et år.
-Mangler per kvadratmeter stoff.
-Antall blodceller i 1 kubikkcentimeter.
-Samtaler per minutt til en telefonsentral.
-Sjokoladeflis til stede i 1 kg kakedeig.
-Antall trær smittet av en viss parasitt i 1 hektar skog.
Merk at disse tilfeldige variablene representerer antall ganger en hendelse inntreffer i en bestemt tidsperiode (samtaler per minutt til telefonsentralen), eller et gitt romområde (mangler på et stoff per kvadratmeter).
Disse hendelsene, som allerede er etablert, er uavhengige av tiden som har gått siden forrige forekomst..
Poisson-fordelingen er en god tilnærming til binomialfordelingen så lenge:
-Prøvestørrelsen er stor: n ≥ 100
-Sannsynlighet p er litt: p ≤ 0,1
- μ er i rekkefølgen av: np ≤ 10
I slike tilfeller er Poisson-fordelingen et utmerket verktøy, siden binomialfordeling kan være vanskelig å bruke i disse tilfellene..
En seismologisk studie bestemte at det i løpet av de siste 100 årene var 93 store jordskjelv rundt om i verden, minst 6,0 på Richters skala - logaritmisk-. Anta at Poisson-fordelingen er en passende modell i dette tilfellet. Finne:
a) Gjennomsnittlig forekomst av store jordskjelv per år.
b) Ja P (y) er sannsynligheten for forekomst Y jordskjelv i løpet av et tilfeldig valgt år, finn følgende sannsynligheter:
P(0), P(1), P (to), P (3), P (4), P (5), P (6) og P (7).
c) De sanne resultatene av studien er følgende:
- 47 år (0 jordskjelv)
- 31 år (1 jordskjelv)
- 13 år (2 jordskjelv)
- 5 år (3 jordskjelv)
- 2 år (4 jordskjelv)
- 0 år (5 jordskjelv)
- 1 år (6 jordskjelv)
- 1 år (7 jordskjelv)
Hvordan sammenlignes disse resultatene med resultatene som er oppnådd i del b? Er Poisson-distribusjonen et godt valg for å modellere disse hendelsene?
a) Jordskjelv er hendelser med sannsynlighet s det er lite, og vi vurderer en begrenset periode på ett år. Gjennomsnittlig antall jordskjelv er:
μ = 93/100 jordskjelv / år = 0,93 jordskjelv per år.
b) For å beregne de etterspurte sannsynlighetene erstattes verdiene i formelen gitt i begynnelsen:
y = 2
μ = 0,93
e = 2,71828
Det er ganske mindre enn P (2).
Resultatene er listet opp nedenfor:
P (0) = 0,395, P (1) = 0,367, P (2) = 0,171, P (3) = 0,0529, P (4) = 0,0123, P (5) = 0,00229, P (6) = 0,000355, P (7) = 0,0000471.
For eksempel kan vi si at det er 39,5% sannsynlighet for at det ikke vil oppstå noe større jordskjelv i et gitt år. Eller at det er 5,29% av tre store jordskjelv som forekommer det året.
c) Frekvensene blir analysert, multiplisert med n = 100 år:
39,5; 36,7; 17.1; 5,29; 1,23; 0,229; 0,0355 og 0,00471.
For eksempel:
- En frekvens på 39,5 indikerer at det på 39,5 av 100 år oppstår 0 store jordskjelv, vi kan si at det er ganske nær det faktiske resultatet på 47 år uten noe større jordskjelv..
La oss sammenligne et annet Poisson-resultat med de faktiske resultatene:
- Den oppnådde verdien på 36,7 betyr at det i en periode på 37 år er et stort jordskjelv. Det faktiske resultatet er at det på 31 år var 1 større jordskjelv, noe som samsvarte med modellen.
- Det forventes 17,1 år med 2 store jordskjelv, og det er kjent at det i løpet av 13 år, som er en nær verdi, faktisk var to store jordskjelv.
Derfor er Poisson-modellen akseptabel i denne saken.
Et selskap anslår at antall komponenter som svikter før de når 100 driftstimer, følger en Poisson-fordeling. Hvis gjennomsnittlig antall feil er 8 på den tiden, finn følgende sannsynligheter:
a) At en komponent svikter på 25 timer.
b) Feil på mindre enn to komponenter på 50 timer.
c) Svikt i minst tre komponenter på 125 timer.
a) Det er kjent at gjennomsnittet av feil i 100 timer er 8, derfor forventes det en kvart feil, det vil si 2 feil i løpet av 25 timer. Dette vil være parameteren μ.
Det blir bedt om sannsynligheten for at en komponent mislykkes, den tilfeldige variabelen er "komponenter som feiler før 25 timer" og verdien er y = 1. Ved å erstatte i sannsynlighetsfunksjonen:
Spørsmålet er imidlertid hvor sannsynlig de er for å mislykkes mindre enn to komponenter i løpet av 50 timer, ikke at nøyaktig to komponenter svikter på 50 timer, derfor må vi legge til sannsynlighetene for at:
-Ingen mislykkes
-Mislykkes bare 1
P (mindre enn 2 komponenter svikter) = P (0) + P (1)
P (mindre enn 2 komponenter feiler) = 0,0183 + 0,0732 = 0.0915
c) At de mislykkes i det minste 3 komponenter på 125 timer, betyr at 3, 4, 5 eller mer kan mislykkes på den tiden.
Sannsynligheten for at det oppstår i det minste en av flere hendelser er lik 1, minus sannsynligheten for at ingen av hendelsene vil inntreffe.
-Den ønskede hendelsen er at 3 eller flere komponenter svikter på 125 timer
-Hvis hendelsen ikke inntreffer, betyr det at færre enn tre komponenter feiler, og sannsynligheten er: P (0) + P (1) + P (2)
Parameteren μ av fordelingen i dette tilfellet er:
μ = 8 + 2 = 10 feil på 125 timer.
P (3 eller flere komponenter svikter) = 1- P (0) - P (1) - P (2) =
Ingen har kommentert denne artikkelen ennå.