De normal distribusjon eller Gaussisk fordeling er sannsynlighetsfordelingen i en kontinuerlig variabel, der sannsynlighetstetthetsfunksjonen er beskrevet av en eksponensiell funksjon av kvadratisk og negativt argument, som gir opphav til en klokkeform.
Navnet på normalfordeling kommer av det faktum at denne fordelingen er den som gjelder for flest mulig situasjoner der noen kontinuerlig tilfeldig variabel er involvert i en gitt gruppe eller populasjon..
Eksempler der normalfordelingen brukes er: høyden på menn eller kvinner, variasjoner i mål av en viss fysisk størrelse eller i målbare psykologiske eller sosiologiske egenskaper som den intellektuelle kvotienten eller forbruksvanene til et bestemt produkt.
På den annen side kalles det en Gaussisk fordeling eller Gaussisk bjelle, fordi det er dette tyske matematiske geniet som er kreditert sin oppdagelse for bruken han ga den for å beskrive den statistiske feilen til astronomiske målinger tilbake til år 1800..
Imidlertid heter det at denne statistiske distribusjonen tidligere ble publisert av en annen stor matematiker med fransk opprinnelse, som Abraham de Moivre, tilbake i år 1733.
Artikkelindeks
Til normalfordelingsfunksjonen i kontinuerlig variabel x, med parametere μ Y σ det er betegnet med:
N (x; μ, σ)
og det er eksplisitt skrevet slik:
N (x; μ, σ) = ∫-∞x f (s; μ, σ) ds
hvor f (u; μ, σ) er sannsynlighetstetthetsfunksjonen:
f (s; μ, σ) = (1 / (σ√ (2π)) Exp (- sto/ (2σto))
Konstanten som multipliserer den eksponensielle funksjonen i sannsynlighetstetthetsfunksjonen kalles normaliseringskonstanten, og den er valgt på en slik måte at:
N (+ ∞, μ, σ) = 1
Det forrige uttrykket sikrer at sannsynligheten for at den tilfeldige variabelen x er mellom -∞ og + ∞ er 1, det vil si 100% sannsynlighet.
Parameter μ er det aritmetiske gjennomsnittet av den kontinuerlige tilfeldige variabelen x y σ standardavviket eller kvadratroten til variansen til den samme variabelen. I tilfelle det μ = 0 Y σ = 1 vi har da standard normalfordeling eller typisk normalfordeling:
N (x; μ = 0, σ = 1)
1 - Hvis en tilfeldig statistisk variabel følger en normalfordeling av sannsynlighetstetthet f (s; μ, σ), mesteparten av dataene er gruppert rundt gjennomsnittsverdien μ og er spredt rundt på en slik måte at litt over ⅔ av dataene er mellom μ - σ Y μ + σ.
2- Standardavviket σ det er alltid positivt.
3- Formen på tetthetsfunksjonen F ligner på en bjelle, og det er grunnen til at denne funksjonen ofte kalles en Gaussisk eller en Gaussisk funksjon.
4- I en gaussisk fordeling sammenfaller gjennomsnittet, medianen og modusen.
5- Bøyningspunktene for sannsynlighetstetthetsfunksjonen ligger nøyaktig ved μ - σ Y μ + σ.
6- Funksjonen f er symmetrisk med hensyn til en akse som går gjennom middelverdien μ y har asymptotisk null for x ⟶ + ∞ og x ⟶ -∞.
7- Jo høyere verdien av σ større spredning, støy eller avstand fra dataene rundt gjennomsnittsverdien. Det vil si til større σ klokkeformen er mer åpen. I stedet σ liten indikerer at terningene er tette mot midten og at formen på bjellen er mer lukket eller spiss.
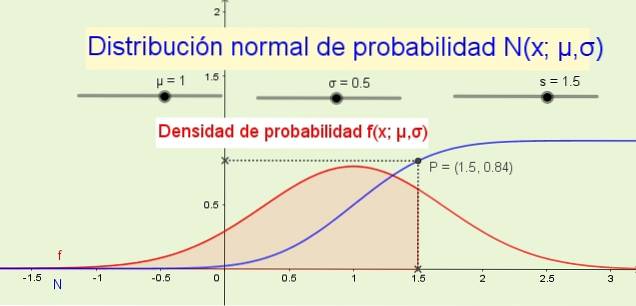
8- Distribusjonsfunksjonen N (x; μ, σ) indikerer sannsynligheten for at den tilfeldige variabelen er mindre enn eller lik x. For eksempel i figur 1 (over) sannsynligheten P for at variabelen x er mindre enn eller lik 1.5 er 84% og tilsvarer arealet under sannsynlighetstetthetsfunksjonen f (x; μ, σ) fra -∞ til x.
9- Hvis dataene følger en normalfordeling, er 68,26% av disse mellom μ - σ Y μ + σ.
10- 95,44% av dataene som følger en normalfordeling er funnet mellom μ - 2σ Y μ + 2σ.
11- 99,74% av dataene som følger en normalfordeling er mellom μ - 3σ Y μ + 3σ.
12- Hvis en tilfeldig variabel x følg en fordeling N (x; μ, σ), deretter variabelen
z = (x - μ) / σ følger standard normalfordeling N (z, 0,1).
Endringen av variabelen x til z Det kalles standardisering eller skriving, og det er veldig nyttig når du bruker tabellene for standardfordelingen på dataene som følger en ikke-standard normalfordeling..
For å bruke normalfordelingen er det nødvendig å gå gjennom beregningen av integralen av sannsynlighetstettheten, noe som fra et analytisk synspunkt ikke er lett, og det ikke alltid er et dataprogram som tillater numerisk beregning. For dette formål brukes tabellene over normaliserte eller standardiserte verdier, noe som ikke er noe mer enn normalfordelingen i saken μ = 0 og σ = 1.
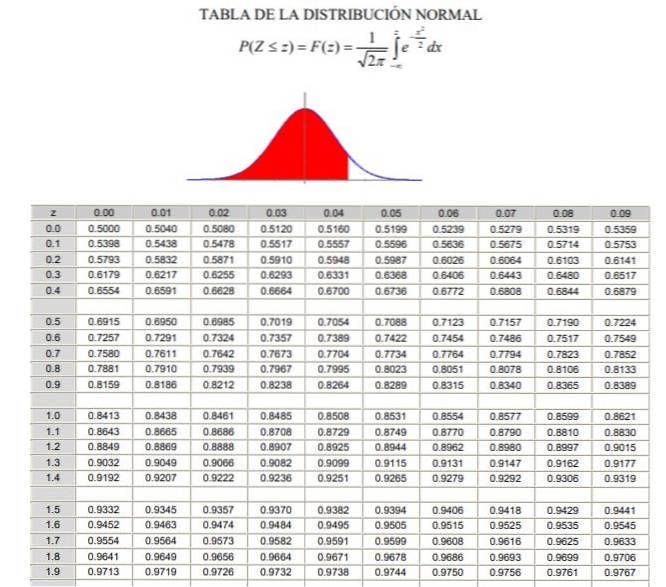
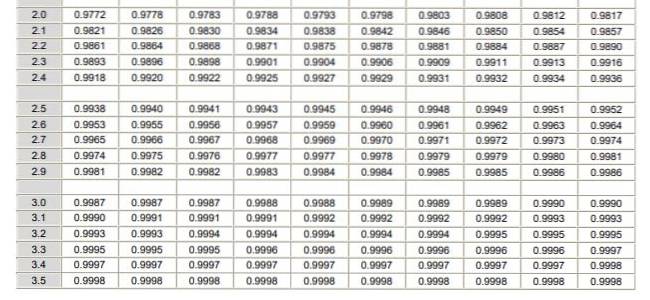
Det skal bemerkes at disse tabellene ikke inkluderer negative verdier. Imidlertid, ved bruk av symmetriegenskapene til den Gaussiske sannsynlighetstetthetsfunksjonen, kan tilsvarende verdier oppnås. I den løste øvelsen vist nedenfor er bruken av tabellen i disse tilfellene indikert.
Anta at du har et sett med tilfeldige data x som følger en normalfordeling av gjennomsnitt 10 og standardavvik 2. Du blir bedt om å finne sannsynligheten for at:
a) Den tilfeldige variabelen x er mindre enn eller lik 8.
b) Er mindre enn eller lik 10.
c) At variabelen x er under 12.
d) Sannsynligheten for at en verdi x er mellom 8 og 12.
Løsning:
a) For å svare på det første spørsmålet må du bare beregne:
N (x; μ, σ)
Med x = 8, μ = 10 Y σ = 2. Vi innser at det er en integral som ikke har en analytisk løsning i elementære funksjoner, men løsningen uttrykkes som en funksjon av feilfunksjonen erf (x).
På den annen side er det muligheten for å løse integralet i numerisk form, som er det mange kalkulatorer, regneark og dataprogrammer som GeoGebra gjør. Følgende figur viser den numeriske løsningen som tilsvarer det første tilfellet:
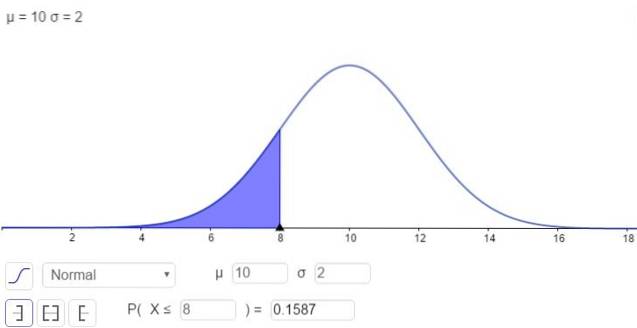
og svaret er at sannsynligheten for at x er under 8 er:
P (x ≤ 8) = N (x = 8; μ = 10, σ = 2) = 0,1587
b) I dette tilfellet prøver vi å finne sannsynligheten for at den tilfeldige variabelen x er under gjennomsnittet, som i dette tilfellet er verdt 10. Svaret krever ingen beregning, siden vi vet at halvparten av dataene er under gjennomsnittet og den andre halvparten over gjennomsnittet. Derfor er svaret:
P (x ≤ 10) = N (x = 10; μ = 10, σ = 2) = 0,5
c) For å svare på dette spørsmålet må du beregne N (x = 12; μ = 10, σ = 2), Dette kan gjøres med en kalkulator som har statistiske funksjoner eller gjennom programvare som GeoGebra:
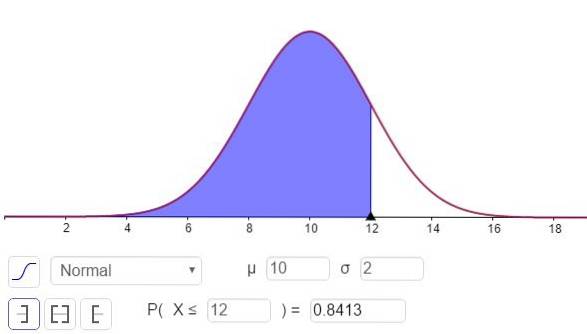
Svaret på del c kan sees i figur 3 og er:
P (x ≤ 12) = N (x = 12; μ = 10, σ = 2) = 0,8413.
d) For å finne sannsynligheten for at den tilfeldige variabelen x er mellom 8 og 12, kan vi bruke resultatene fra del a og c på følgende måte:
P (8 ≤ x ≤ 12) = P (x ≤ 12) - P (x ≤ 8) = 0,8413 - 0,1587 = 0,6826 = 68,26%.
Gjennomsnittsprisen på selskapets aksjer er $ 25 med et standardavvik på $ 4. Bestem sannsynligheten for at:
a) En handling koster mindre enn $ 20.
b) Det koster mer enn $ 30.
c) Prisen er mellom $ 20 og $ 30.
Bruk standard normalfordelingstabeller for å finne svar.
Løsning:
For å kunne bruke tabellene er det nødvendig å overføre til den normaliserte eller typte z-variabelen:
$ 20 i den normaliserte variabelen er lik z = ($ 20 - $ 25) / $ 4 = -5/4 = -1,25 og
$ 30 i den normaliserte variabelen er lik z = ($ 30 - $ 25) / $ 4 = +5/4 = +1,25.
a) $ 20 tilsvarer -1,25 i den normaliserte variabelen, men tabellen har ikke negative verdier, så vi plasserer verdien +1,25 som gir verdien på 0,8944.
Hvis 0,5 trekkes fra denne verdien, vil resultatet bli området mellom 0 og 1,25 som for øvrig er identisk (ved symmetri) med området mellom -1,25 og 0. Resultatet av subtraksjonen er 0,8944 - 0,5 = 0,3944 som er området mellom -1,25 og 0.
Men området fra -∞ til -1,25 er av interesse, som vil være 0,5 - 0,3944 = 0,1056. Det konkluderes derfor med at sannsynligheten for at en aksje er under $ 20 er 10,56%.
b) $ 30 i den typede variabelen z er 1,25. For denne verdien vises tallet 0,8944 i tabellen, som tilsvarer området fra -∞ til +1,25. Arealet mellom +1,25 og + ∞ er (1 - 0,8944) = 0,1056. Det vil si at sannsynligheten for at en aksje koster mer enn $ 30 er 10,56%.
c) Sannsynligheten for at en handling koster mellom $ 20 og $ 30 vil bli beregnet som følger:
100% -10,56% - 10,56% = 78,88%
Ingen har kommentert denne artikkelen ennå.