
Kontinuerlig jevn fordelingskarakteristikk, eksempler, applikasjoner
En tilfeldig variabel har a kontinuerlig jevn fordeling hvis sannsynligheten for at den får en verdi innen et endelig intervall [a, b], er den samme for et hvilket som helst delintervall med samme lengde.
Denne fordelingen er analog med den diskrete ensartede fordelingen, som tildelte samme sannsynlighet for hvert resultat av det tilfeldige eksperimentet, men i dette tilfellet er variabelen som skal vurderes kontinuerlig. Eksperimentet som består av å velge et reelt tall tilfeldig, mellom verdiene a og b, følger for eksempel den jevne fordelingen. Her er grafen:
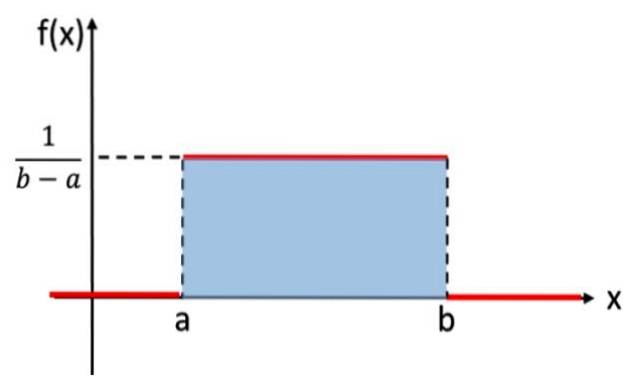
I matematisk notasjon har den kontinuerlige ensartede fordelingen en tetthetsfunksjon definert som en stykkevis eller stykkevis funksjon, som kan skrives som:
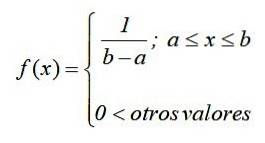
Grafen til denne funksjonen, kjent som tetthetskurve eller funksjon, er et rektangel, derfor er den kontinuerlige ensartede fordelingen også kjent som rektangulært oppsett y er den enkleste av kontinuerlige distribusjoner.
Området under grafen for en sannsynlighetsfordeling er lik 1 og tar alltid positive verdier. Den ensartede fordelingen oppfyller disse kriteriene. Det er ikke nødvendig å integrere direkte for å kontrollere at området er 1, siden området til det skyggelagte rektangelet i figur 1 kan beregnes ved hjelp av formelen:
Areal = base x høyde = (b - a) x [1 / (b - a)] = 1
Å kjenne området under tetthetskurven er veldig viktig, fordi det er et forhold mellom området og sannsynligheten for forekomst av en hendelse, som for denne fordelingen bestemmes i neste avsnitt.
Kjennetegn ved kontinuerlig jevn fordeling
Den kontinuerlige jevne fordelingen er preget av sin:
Tetthetsfunksjon
La X være den kontinuerlige tilfeldige variabelen, som tilhører intervallet [a, b], og deretter:

Distribusjonsfunksjon
Distribusjonsfunksjonen beregner sannsynligheten for at den tilfeldige variabelen X tar en verdi x blant de mulige verdiene til intervallet [a, b]. For en kontinuerlig fordeling beregnes det generelt slik:

Når det gjelder kontinuerlig jevn fordeling, er sannsynligheten F (x) lik arealet til rektangelet hvis base er (x-a) og høyden er (b-a):

Matematisk, hvis F (x) = Pr (X = x) er følgende funksjon etablert i deler, i henhold til forrige resultat:

På denne måten bekreftes det som ble sagt tidligere: sannsynligheten avhenger bare av verdien av (x-a) og ikke av plasseringen i intervallet [a, b]. Grafen for fordelingsfunksjonen er:
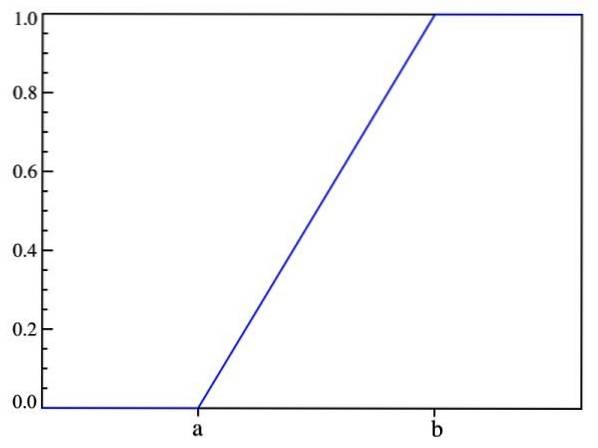
Forventet verdi, avvik og standardavvik
Etter å ha gjort mange eksperimenter med den kontinuerlige tilfeldige variabelen, kalles den gjennomsnittlige verdien forventet verdi, betegnes som E (X) og beregnes av følgende integral:

V (X) = E (Xto) - E (X)to
Derfor:


D (X) = √ V (X)

Median, modus, symmetri og kurtose
Det kan enkelt verifiseres at medianen, som er den sentrale verdien av den ensartede fordelingen, er lik gjennomsnittet, og siden det ikke er noen verdi som gjentas mer enn andre, siden alle er like sannsynlige i intervallet [a, b] , mote eksisterer ikke.
Når det gjelder symmetri, er den jevne fordelingen symmetrisk og kurtosen, som er i hvilken grad verdiene er konsentrert rundt sentrum, er -6/5.
Eksempler
Ulike situasjoner kan modelleres gjennom kontinuerlig distribusjon, og dermed kan deres atferd forutsies. Her er noen eksempler:
Eksempel 1
Et selskap som leverer elektrisk service, gir spenningsnivåer jevnt fordelt, mellom 123,0 V og 125,0 V. Dette betyr at det i husuttaket er mulig å oppnå hvilken som helst spenningsverdi som tilhører det området..
Så, som vist ovenfor, er grafen for tetthetsfunksjonen rektangelet i rødt:

Det er veldig enkelt å beregne sannsynligheten for å ha en spenning innenfor det gitte intervallet, for eksempel, hva er sannsynligheten for at selskapet sender en spenning lavere enn 123,5 V?
Denne sannsynligheten er lik arealet av rektangelet skyggelagt i blått:
P (X<123.5) = (123.5 −123.0)x 0.5 = 0.25
Og hva er sannsynligheten for at spenningen som er levert er større enn 124,0 V?
Siden det totale arealet er lik 1, er sannsynligheten som søkes:
P (X> 124,0 V) = 1 - (1 × 0,5) = 0,5
Det er fornuftig, siden 124.0 er nettopp verdien i midten av intervallet.
Eksempel 2
En viss tilfeldig variabel X har en jevn fordeling i intervallet [0,100]. Bestemme seg for:
a) Sannsynligheten for at verdien av X er mindre enn 22.
b) Sannsynligheten for at X tar verdier mellom 20 og 35.
c) Den forventede verdien, variansen og standardavviket til denne fordelingen.
Svar til
Det bestemmes på samme måte som forrige eksempel, men først må vi bestemme høyden på rektangelet, og huske at det totale arealet må være lik 1:
Areal = 100 × høyde = 1
Derfor har rektangelet en høyde lik 1/100 = 0.01
P (X<22) = 22×0.01 = 0.22
Svar b
Den etterspurte sannsynligheten er lik arealet til rektangelet hvis bredde er (35 - 20) og hvis høyde er 0,01:
P (22 Hvis du foretrekker å gå direkte til distribusjonsfunksjonen gitt ovenfor, må du bare erstatte verdiene i: P (20≤X≤35) = F (35) -F (20) Med F (x) gitt av: F (x) = (x-a) / (b-a) Verdiene du skal angi er: a = 0 b = 100 F (35) = (35-0) / (100-0) = 0,35 F (20) = (20-0) / (100-0) = 0,20 P (20≤X≤35) = 0,35-0,20 = 0,15 Den forventede verdien er: E (X) = (a + b) / 2 = (100 + 0) / 2 = 50 Avviket er: V (X) = (b-a)to/ 12 = (100-0)to/ 12 = 833,33 Og standardavviket er: D (X) = √833,33 = 28,87 Denne fordelingen er nyttig når du utfører statistiske simuleringsprosesser eller når du arbeider med hendelser der hyppigheten av forekomst er vanlig.. Noen programmeringsspråk genererer tilfeldige tall mellom 0 og 1, og som det fremgår av de foregående eksemplene, er sannsynlighetsfordelingen fulgt ensartet. I dette tilfellet er intervallet å vurdere [0,1]. Hvis du har et eksperiment der hendelsene har regelmessighet, som forklart før, kan du i prinsippet tildele hver enkelt samme sannsynlighet for forekomst. I dette tilfellet gir den sannsynlige modellen for ensartet distribusjon informasjon for analysen.. Den ensartede fordelingen brukes også til å avrunde forskjellene mellom de observerte verdiene og de reelle verdiene til en variabel, forutsatt en jevn fordeling av feilen i et gitt intervall, i henhold til avrunding, vanligvis fra -0,5 til +0,5.Svar c
applikasjoner
Tilfeldig antallgenerering
Prøvetaking av vilkårlige fordelinger
Avrunding av feil
Referanser


Ingen har kommentert denne artikkelen ennå.