Generell ligning av en linje hvis skråning er lik 2/3

Den generelle ligningen til en linje L er følgende: Ax + By + C = 0, hvor A, B og C er konstanter, x er den uavhengige variabelen og og den avhengige variabelen.

Skråningen til en linje, vanligvis betegnet med bokstaven m, som går gjennom punktene P = (x1, y1) og Q = (x0, y0) er følgende kvotient m: = (y1-y0) / (x1 -x0 ).

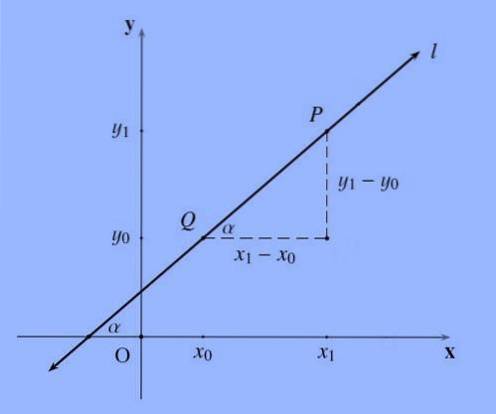
Skråningen til en linje, representerer på en viss måte hellingen; Mer formelt er hellingen til en linje tangenten til vinkelen den danner med X-aksen..

Det bør bemerkes at rekkefølgen poengene er navngitt er likegyldig, siden (y0-y1) / (x0-x1) = - (y1-y0) / (- (x1-x0)) = (y1-y0) / (x1-x0).

Helling av en linje

Hvis det er kjent to punkter som en linje går gjennom, er det enkelt å beregne helningen. Men hva om disse punktene ikke er kjent?

Gitt den generelle ligningen til en linje Ax + By + C = 0, er hellingen m = -A / B.

Hva er den generelle ligningen til en linje der hellingen er 2/3?

Siden hellingen på linjen er 2/3, blir likheten -A / B = 2/3 etablert, som vi kan se at A = -2 og B = 3. Så den generelle ligningen til en linje med stigning lik 2/3 er -2x + 3y + C = 0.

Det bør avklares at hvis A = 2 og B = -3 velges, vil samme ligning oppnås. Faktisk er 2x-3y + C = 0, som er lik den forrige ganget med -1. Tegnet på C spiller ingen rolle, da det er en generell konstant.

En annen observasjon som kan gjøres er at for A = -4 og B = 6 oppnås samme linje, til tross for at deres generelle ligning er forskjellig. I dette tilfellet er den generelle ligningen -4x + 6y + C = 0.

Er det andre måter å finne linjens generelle ligning?

Svaret er ja. Hvis hellingen til en linje er kjent, er det to måter, i tillegg til den forrige, å finne den generelle ligningen.

For dette brukes Point-Slope-ligningen og Shear-Slope-ligningen..

-Point-Slope-ligningen: hvis m er hellingen til en linje og P = (x0, y0) et punkt den går gjennom, kalles ligningen y-y0 = m (x-x0) Point-Slope-ligningen.

-Shear-Slope-ligningen: hvis m er hellingen til en linje og (0, b) er linjens kutt med Y-aksen, blir ligningen y = mx + b kalt Shear-Slope-ligningen.

Ved å bruke det første tilfellet oppnås det at Point-Slope-ligningen til en linje med hellingen er 2/3 er gitt av uttrykket y-y0 = (2/3) (x-x0).

For å komme til den generelle ligningen, multipliser med 3 på begge sider, og alle ordene er gruppert på den ene siden av likheten, som det oppnås med at -2x + 3y + (2 × 0-3y0) = 0 er den generelle ligningen av linjen, der C = 2 × 0-3y0.

Hvis det andre tilfellet brukes, oppnås det at ligningen Cut-Slope av en linje med hellingen er 2/3 er y = (2/3) x + b.

Igjen, multiplisere med 3 på begge sider, og gruppere alle variablene, får vi -2x + 3y-3b = 0. Sistnevnte er den generelle ligningen på linjen der C = -3b.

Når man ser nøye på begge tilfeller, kan det sees at det andre tilfellet bare er et spesielt tilfelle av det første (når x0 = 0).

Referanser

1. Fleming, W., & Varberg, D. E. (1989). Precalculus matematikk. Prentice Hall PTR.
2. Fleming, W., & Varberg, D. E. (1989). Precalculus matematikk: en problemløsende tilnærming (2, Illustrert utg.). Michigan: Prentice Hall.
3. Kishan, H. (2005). Integral Calculus. Atlantic Publishers & Distributors.
4. Larson, R. (2010). Precalculus (8. utgave). Cengage læring.
5. Leal, J. M., og Viloria, N. G. (2005). Flyanalytisk geometri. Mérida - Venezuela: Redaksjonelt Venezolana C. A.
6. Pérez, C. D. (2006). Forberegning. Pearson Education.
7. Saenz, J. (2005). Differensiell kalkulator med tidlige transcendente funksjoner for vitenskap og ingeniørfag (Andre utgave utg.). Hypotenuse.
8. Sullivan, M. (1997). Forberegning. Pearson Education.