De første grad eller lineære ligninger med en ukjent er de som kan uttrykkes som summen av to termer, som følger:
øks + b = 0
Hvor a og b, med til ≠ 0, er reelle tall R eller også komplekse C. For å løse det, blir termer transponert, noe som betyr å endre termer fra den ene siden av likheten til den andre.
For å løse det ukjente er begrepet + b transponert, som må gå til høyre side av likheten med endret tegn.
øks = -b
Da tømmes verdien på x, slik:
x = - b / a
Som et eksempel skal vi løse følgende ligning:
6x - 5 = 4
Vi transponerer -5-begrepet til høyre med et endret tegn:
6x = 4 + 5
Dette tilsvarer å legge 5 til begge sider av den opprinnelige ligningen:
6x - 5 + 5 = 4 + 5 → 6x = 9
Og nå løser vi det ukjente "x":
x = 9/6 = 3/2
Som tilsvarer å dele begge sider av likheten med 6. Så vi kan bruke følgende for å oppnå løsningen:
-Den samme mengden kan legges til eller trekkes fra begge sider av likheten i en ligning, uten å endre den.
-Du kan også multiplisere (eller dele) med samme mengde alle vilkårene både til venstre og til høyre for ligningen.
-Og hvis begge medlemmene av en ligning løftes til samme makt, blir heller ikke likheten endret.
Artikkelindeks
Løsningen av en ligning av første grad er også kjent som roten. Det er verdien av x som konverterer det opprinnelige uttrykket til en likhet. For eksempel i:
5x = 8x - 15
Hvis vi erstatter x = 5 i denne ligningen, får vi:
5⋅5 = 8⋅5 - 15
25 = 40 - 15
25 = 25
Siden lineære ligninger av første grad kommer i mange former, som noen ganger ikke er åpenbare, er det en rekke generelle regler som inkluderer forskjellige algebraiske manipulasjoner, for å finne verdien av det ukjente:
-Først og fremst, hvis det er angitt operasjoner, bør de utføres.
-Gruppering av symboler som parenteser, firkantede parenteser og parenteser, hvis noen, bør fjernes med beholder passende tegn.
-Vilkårene er transponert for å plassere alle de som inneholder det ukjente på den ene siden av likheten, og de som ikke inneholder det på den andre.
-Da reduseres alle like vilkår for å komme til skjemaet øks = -b.
-Og det siste trinnet er å fjerne det ukjente.
Første grads ligning hevet i begynnelsen kan avledes fra ligningen til linjen y = mx + c, noe som gjør y = 0. Den resulterende verdien på x tilsvarer krysset mellom linjen og den horisontale aksen.
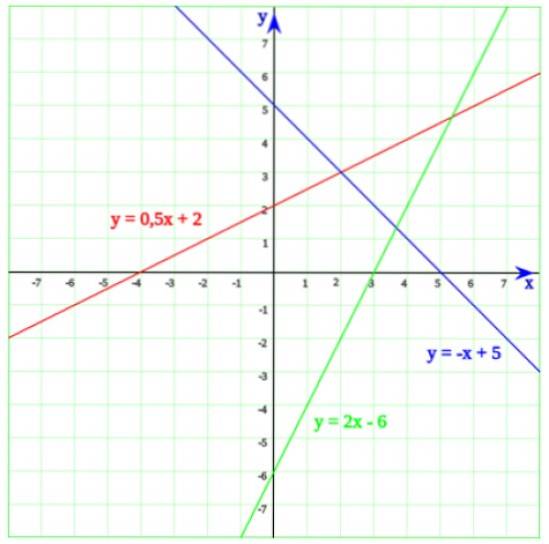
I den følgende figuren er det tre linjer. Starter med den grønne linjen, hvis ligning er:
y = 2x - 6
Gjør du y = 0 i ligningen til linjen, oppnås første grads ligning:
2x - 6 = 0
Hvis løsning er x = 6/2 = 3. Nå når vi detaljerer grafen, er det lett å innse at linjen i virkeligheten skjærer den horisontale aksen ved x = 3.
Den blå linjen krysser x-aksen ved x = 5, som er løsningen på ligningen -x + 5 = 0. Til slutt krysser linjen hvis ligning er y = 0.5x + 2 x-aksen ved x = - 4 , som lett sees fra ligningen til første grad:
0,5 x + 2 = 0
x = 2 / 0,5 = 4
Det er de som det ikke er noen nevnere i, for eksempel:
21 - 6x = 27 - 8x
Løsningen din er:
-6x + 8x = 27 - 21
2x = 6
x = 3
Disse ligningene inneholder minst en annen nevner enn 1. For å løse dem, er det tilrådelig å multiplisere alle uttrykkene med det minst vanlige multiple (LCM) av nevnerne, for å eliminere dem.
Følgende ligning er brøkstype:
Siden disse tallene er små, er det ikke vanskelig å se at m.c.m (6, 8,12) = 24. Dette resultatet oppnås lett ved å uttrykke tallene som et produkt av primtall eller deres krefter, la oss se:
6 = 3,2
8 = 23
12 = 2to⋅3
Det minst vanlige multiplumet bestemmes ved å multiplisere de vanlige og uvanlige faktorene 6, 8 og 12 med deres største eksponent, deretter:
lcm (6,8,12) = 23 ⋅3 = 8 × 3 = 24
Siden vi har minst vanlig multiplum, må det multipliseres med hver av begrepene i ligningen:
4 (x + 5) -3 (2x + 3) = 2 (1-5x)
Vi bruker distribusjonsegenskapene:
4x + 20 - 6x -9 = 2 - 10x
Alle begrepene som inneholder den ukjente "x" er gruppert på venstre side av likheten, og etterlater de uavhengige eller numeriske begrepene på høyre side:
4x - 6x + 10 x = 2 +9 - 20
8x = -9
x = - 9/8
De er lineære ligninger med en ukjent, som imidlertid er ledsaget av bokstavelige koeffisienter (bokstaver). Disse bokstavene blir behandlet på samme måte som tall. Et eksempel på en bokstavelig første grads ligning er:
-3ax + 2a = 5x - b
Denne ligningen løses på samme måte som om de uavhengige begrepene og koeffisientene var numeriske:
-3ax - 5x = - b - 2a
Faktorering av det ukjente "x":
x (-3a - 5) = - b - 2a
x = (- b - 2a) / (-3a - 5) → x = (2a + b) / (3a + 5)
Ligningssystemer består av et sett med ligninger med to eller flere ukjente. Løsningen til systemet består av verdier som tilfredsstiller ligningene samtidig, og for å bestemme det utvetydig, må det være en ligning for hver ukjent.
Den generelle formen for et system av m lineære ligninger med n ukjente er:
tilellevex1 + til12xto +… til1nxn = b1
tiltjueenx1 + til22xto +… til2nxn = bto
...
tilm1x1 + tilm2xto +… tilmnxn = bm
Hvis systemet har en løsning, sies det å være det kompatibel bestemt, når det er et uendelig sett med verdier som tilfredsstiller det ubestemt kompatibel, og til slutt hvis den ikke har noen løsning, er den det uforenlig.
Ved løsning av systemer med lineære ligninger brukes flere metoder: reduksjon, substitusjon, utjevning, grafiske metoder, Gauss-Jordan eliminering og bruk av determinanter er blant de mest brukte. Men det er andre algoritmer for å nå løsningen, mer praktisk for systemer med mange ligninger og ukjente.
Et eksempel på et system med lineære ligninger med to ukjente er:
8x - 5 = 7y - 9
6x = 3y + 6
Løsningen på dette systemet presenteres senere i avsnittet om løste øvelser..
Den absolutte verdien av et reelt tall er avstanden mellom plasseringen på tallinjen og 0 på tallinjen. Siden det er en avstand, er verdien alltid positiv.
Den absolutte verdien til et tall er betegnet med modulstengene: │x│. Den absolutte verdien av et positivt eller negativt tall er alltid positiv, for eksempel:
│ + 8│ = 8
│-3│ = 3
I en absolutt verdiligning er det ukjente mellom modulstenger. La oss vurdere følgende enkle ligning:
│x│ = 10
Det er to muligheter, den første er at x er et positivt tall, i så fall har vi:
x = 10
Og den andre muligheten er at x er et negativt tall, i dette tilfellet:
x = -10
Dette er løsningene i denne ligningen. La oss nå se på et annet eksempel:
│x + 6│ = 11
Mengden inne i stolpene kan være positiv, så:
x + 6 = 11
x = 11 -6 = 5
Eller det kan være negativt. I så fall:
-(x + 6) = 11
-x - 6 = 11 ⇒ -x = 11 + 6 = 17
Og verdien av det ukjente er:
x = -17
Denne absolutte verdi ligningen har derfor to løsninger: x1 = 5 og xto = -17. Vi kan sjekke at begge løsningene fører til en likhet i den opprinnelige ligningen:
│5 + 6│ = 11
│11│ = 11
Y
│-17 + 6│ = 11
│-11│ = 11
Løs følgende system med lineære ligninger med to ukjente:
8x - 5 = 7y -9
6x = 3y + 6
Som det er foreslått, er dette systemet ideelt for å bruke substitusjonsmetoden, siden i den andre ligningen det ukjente x er nesten klar for klarering:
x = (3y + 6) / 6
Og det kan umiddelbart erstattes i den første ligningen, som deretter blir en første grads ligning med ukjent "y":
8 [(3y + 6) / 6] - 5 = 7y - 9
Nevneren kan fjernes ved å multiplisere hvert begrep med 6:
6. 8⋅ [(3y + 6) / 6] - 6,5 = 6,77-6. 9
8⋅ (3y + 6) - 30 = 42y - 54
Å bruke distribusjonseiendommen i første periode på retten til likestilling:
24 år + 48-30 = 42 år - 54 ⇒ 24 år + 18 = 42 år - 54
Ligningen kan forenkles, siden alle koeffisientene er multipler av 6:
4y + 3 = 7y - 9
-3y = -12
y = 4
Med dette resultatet går vi til clearing av x:
x = (3y +6) / 6 → x = (12 + 6) / 6 = 3
Løs følgende ligning:
Produktene vises i denne ligningen, og i henhold til instruksjonene gitt i begynnelsen må de utvikles først:
3x - 10x +14 = 5x + 36x + 12
Så blir alle begrepene som inneholder ukjente ført til venstre side av likestillingen, og til høyre vil være de uavhengige begrepene:
3x - 10x - 5x - 36x = 12-14
-48x = -2
x = 1/24
Å legge til de tre innvendige vinklene i en trekant gir 180º. Major overskrider mindre med 35 °, og sistnevnte overskrider igjen med 20 ° forskjellen mellom dur og medium. Hva er vinklene??
Vi vil kalle “x” for større vinkel, “y” den midterste og “z” den minste. Når uttalelsen bekrefter at summen av dem er 180 º, kan det skrives:
x + y + z = 180
Da vet vi at jo større enn mindre enn 35º, kan vi skrive dette slik:
x = z + 35
Til slutt overstiger den minste forskjellen mellom den største og den midterste med 20º:
z = x - y + 20
Vi har et system med 3 ligninger og 3 ukjente:
x + y + z = 180
x = z + 35
z = x - y + 20
Løsning for z fra den første ligningen vi har:
z = 180 - x - y
Matcher med det tredje:
180 - x - y = x - y + 20
Å passere de ukjente til venstre som alltid:
-x - y - x + y = 20 - 180
"Y" avbrytes og forblir:
-2x = - 160
x = 80º
Fra den andre ligningen finner vi verdien av z:
z = x - 35 = 80 - 35 = 45º
Og verdien av y er funnet fra første eller tredje:
y = 180 - x - z = 180 - 80 - 45 = 55º
Ingen har kommentert denne artikkelen ennå.