
Rotasjonsbalanseformler og ligninger, eksempler, øvelser

En utvidet kropp er oppgitt å være i rotasjonsbalanse når summen av momentene som virker på den er null. Dette betyr ikke at objektet nødvendigvis er i ro, men heller at det ikke er noen nettotendens til å endre sin bevegelsestilstand for en annen..
Et objekt som beveger seg med konstant hastighet gjør det langs en rett linje, og vi kan vurdere det i rotasjonsvekt. Nå roterer objekter fordi det er krefter som virker på dem på en slik måte at en rotasjon oppstår. Evnen til en kraft til å produsere rotasjon, kalt moment eller torca, avhenger ikke bare av intensiteten til kraften, men også av hvor den påføres.

Vi kjenner igjen dette umiddelbart når en lukket dør skal åpnes: det blir aldri brukt kraft nær hengslene, men vekk fra dem, det er derfor håndtaket plasseres så langt som mulig, på motsatt side av døren.
Dørens rotasjonsakse går gjennom hengslene. Å insistere på å skyve den veldig nær hengslene, tar det en stor innsats for å få døren til å bevege seg litt..
I litteraturen er dreiemoment funnet under forskjellige navn: dreiemoment, torsjon, moment av en kraft og dreiemoment. De er alle synonyme.
Så vi trenger å kjenne dreiemomentene som virker på et objekt for å etablere rotasjonsvektstilstanden.
Artikkelindeks
- 1 Tilstand for rotasjonsvekt
- 1.1 Dreiemoment eller moment av en kraft
- 2 Formler og ligninger
- 3 eksempler
- 4 Øvelse løst
- 5 Referanser
Rotasjonsvektstilstand
Rotasjonsvektstilstanden er:
Summen av alle momentene eller dreiemomentene som virker på en kropp, beregnet i forhold til hvilken som helst akse, må være null.
Det aktuelle objektet må strekkes, siden partikler per definisjon bare har translasjonell likevekt.
Det kan være krefter påført kroppen og fortsatt eksisterer rotasjonsvekt, så lenge kreftene ikke får den til å rotere.
Det kan også være bevegelse, til og med akselerert, men alltid langs en rett linje, siden ikke alle krefter forårsaker dreiemomenter. Disse vises når kreftene ikke alle handler i samme handlingslinje..
Moment eller moment av en kraft
Dreiemoment er betegnet med det greske brevet τ, på Fet skrift fordi det er en vektor og dermed skiller vi den fra størrelsen eller modulen, som er en skalar. Det avhenger av den påførte kraften F, vektor r som er rettet fra rotasjonsaksen O til kraftens påføringspunkt og til slutt fra vinkelen mellom disse to vektorene.
Vektorproduktet etablerer det passende forholdet mellom disse mengdene:
τ = r x F
Og dreiemomentmodulen, betegnet uten fet skrift, er:
τ = r⋅F⋅sen θ
Hvor θ er vinkelen mellom r Y F. Enhetene til dreiemoment er ganske enkelt N⋅m i det internasjonale systemet.
På figuren er det en skiftenøkkel som den er ment å vri en mutter mot klokken (mot klokken). For dette er det testet med to krefter FTIL Y FB.
FTIL er nærmere O og har en vektor rTIL eller kortere spakarm, derfor produserer den ikke så mye dreiemoment som kraften FB, som har lik størrelse, men har en vektor rB større.
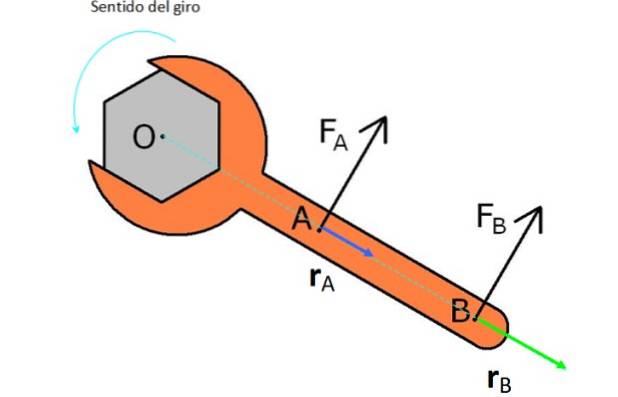
Merk at hvis du vil vri mutteren med urviseren, må du bruke kreftene i motsatt retning slik de vises i figuren..
Retning og følelse av dreiemoment
Ettersom dreiemomentet skyldes kryssproduktet mellom kraft- og posisjonsvektorene, og disse er i skiftenøkkelens plan, må dreiemomentet være en vektor vinkelrett på nevnte plan, det vil si rettet mot leseren eller mot innsiden av side.
Etter konvensjonen er dreiemoment positivt hvis det roterer mot klokken, og negativt hvis det roterer med klokken..
Retningen og følelsen av det resulterende dreiemomentet bestemmes enkelt av høyre håndregel vist nedenfor:
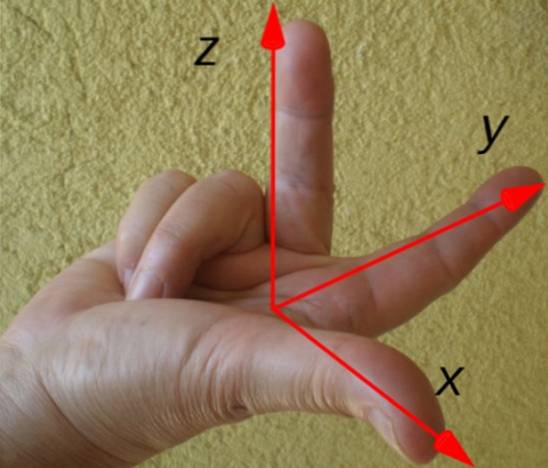
Pekefingeren peker i henhold til posisjonsvektoren r, langfinger etter styrke F og tommelen peker retning og følelse av dreiemoment τ. I dette eksemplet er dreiemomentet rettet langs x-aksen, i henhold til koordinataksene.
Formler og ligninger
Hvis dreiemoment virker på kroppen τ1, τto, τ3 ... τJeg, netto eller resulterende dreiemoment τn er vektorsummen av dem alle:
τn = τ1+ τto + τ3 +... τJeg
Med summeringsnotasjon gjenstår det:
τn = ∑ τJeg
Likevektstilstanden uttrykkes matematisk som følger:
τn = 0
O brønn:
∑ τJeg = 0
Hvor dreiemomentet τ, med hensyn til en bestemt akse O, beregnes den av:
τ = r x F
Og hvis størrelse er:
τ = r⋅F⋅sen θ
Eksempler
-Hos mennesker og dyr er vekt en kraft som kan forårsake dreiemoment og spinn og fall.
Folk opprettholder generelt en holdning slik at når de går, holder de dem i rotasjonsbalanse, med mindre de praktiserer sportsaktiviteter, som gymnastikk, skøyter eller sport generelt..
-To gutter som klarte å holde seg vannrette i rocker eller opp og ned er i rotasjonsvekt.
-Når balansepanene er balansert, er systemet i rotasjonsvekt.
-Skilt og trafikklys som henger på gater og alléer er også i rotasjonsvekt. Hvis kablene som holder dem går i stykker, går denne balansen tapt og skiltet henger eller faller..
-Hengebroer som Golden Gate i San Francisco og broen i figur 1.
Treningen løst
Støttelinjen vist på figuren er veldig lett. Styrken som støtten utøver er F og ekstrem høyre brukes kraft TIL.
Det blir bedt om å beregne størrelsen på disse kreftene med tanke på at systemet er i translasjons- og rotasjonsvekt.

Løsning
Siden systemet ikke beveger seg, avbrytes summeringen av krefter. De er alle vertikale og kan bearbeides i størrelsesorden. Den positive retningen er oppover og den negative retningen er nedover, derfor:
F - 80 - A = 0
Nå er den roterende likevektstilstanden brukt, som vi må velge en vilkårlig rotasjonsakse for. I dette tilfellet er det valgt helt til høyre, slik at vektoren rTIL er null, på denne måten dreiemomentet utøvd av TIL, men bare de av F og styrken til venstre.
Dreiemomentet produsert av F er, i henhold til høyre regel og koordinatsystemet vist:
τF = rF x F = 0,9 F (-k) N.m
Den er rettet mot innsiden av skjermen og har et negativt tegn. Mens dreiemomentet produsert av 80 N kraften er:
τ = 80 x 1,20 (k) N⋅m = 96 (k) Nm
Dette dreiemomentet ledes bort fra skjermen og tildeles et positivt tegn. Hvordan det er rotasjonsvekt:
96 - 0,9 ° F = 0
Størrelsen på F Det er:
F = (96 / 0,9) N = 106,7 N
Og siden systemet er i translasjonell likevekt, avbrytes summen av kreftene. Dette lar oss løse størrelsen på TIL:
F - A - 80 N = 0
Derfor:
A = 106,7 - 80 N = 26,7 N.
Referanser
- Rex, A. 2011. Fundamentals of Physics. Pearson.
- Serway, R., Jewett, J. (2008). Fysikk for naturvitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning.
- Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 1. Pearson.
- Tipler, P. (2006) Fysikk for vitenskap og teknologi. 5. utg. Bind 1. Redaksjonell Reverté.
- Tippens, P. 2011. Fysikk: Konsepter og applikasjoner. 7. utgave. Mcgraw hill.



Ingen har kommentert denne artikkelen ennå.