
Bestemmelse av translasjonell likevekt, applikasjoner, eksempler
De translasjonell likevekt Det er en tilstand der et objekt som en helhet blir funnet når alle kreftene som virker på det kompenseres, noe som resulterer i en null nettokraft. Matematisk tilsvarer å si at F1+ Fto + F3 +…. = 0, hvor F1, Fto, F3... de involverte styrkene.
Det at et legeme er i translasjonell likevekt betyr ikke at det nødvendigvis er i ro. Dette er et spesielt tilfelle av definisjonen gitt ovenfor. Objektet kan være i bevegelse, men i fravær av akselerasjon vil dette være en ensartet rettlinjet bevegelse.

Så hvis kroppen er i ro, fortsetter den slik. Og hvis den allerede har bevegelse, vil den ha konstant hastighet. Generelt er bevegelsen til ethvert objekt en sammensetning av oversettelser og rotasjoner. Oversettelser kan være som vist i figur 2: lineær eller krumlinjær.
Men hvis et av objektets punkter er løst, er den eneste sjansen den har til å bevege seg å rotere. Et eksempel på dette er en CD, hvis senter er løst. CD-en har muligheten til å rotere rundt en akse som går gjennom det punktet, men ikke å oversette.
Når gjenstander har faste punkter eller støttes på overflater, snakker vi om lenker. Koblingene samhandler og begrenser bevegelsene som objektet er i stand til å gjøre.
Artikkelindeks
- 1 Bestemmelse av translasjonell likevekt
- 1.1 Rotere et objekt
- 1.2 Definisjon av dreiemoment
- 1.3 likevektsforhold
- 2 Søknader
- 3 Eksempler på translasjonell likevekt
- 3.1 Løsning
- 4 Referanser
Bestemmelse av translasjonell likevekt
For en partikkel i likevekt er det gyldig å sikre at:
FR = 0
Eller i summeringsnotasjon:
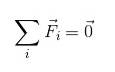
Det er klart at for at et legeme skal være i translationell likevekt, må kreftene som virker på det kompenseres på en eller annen måte, slik at deres resulterende er null..
På denne måten vil ikke objektet oppleve akselerasjon, og alle partiklene er i ro eller gjennomgår rettlinjede oversettelser med konstant hastighet..
Nå hvis objekter kan rotere, vil de generelt. Derfor består de fleste bevegelsene av kombinasjoner av oversettelse og rotasjon..
Rotere et objekt
Når rotasjonsbalanse er viktig, kan det være nødvendig å sikre at objektet ikke roterer. Da er det nødvendig å studere om det er moment eller øyeblikk som virker på det.
Dreiemoment er vektornes størrelse som rotasjonene avhenger av. Det krever at en kraft påføres, men kraftens påføringspunkt er også viktig. For å avklare ideen, vurder et utvidet objekt som en styrke virker på F og la oss se om den er i stand til å produsere en rotasjon rundt en akse O.
Det er allerede intuert at når du skyver objektet på punkt P med kraften F, det er mulig å rotere det rundt punkt O, roterende mot klokken. Men retningen kraften påføres i er også viktig. For eksempel vil ikke kraften som brukes på figuren i midten, få objektet til å rotere, selv om det absolutt kan bevege det..
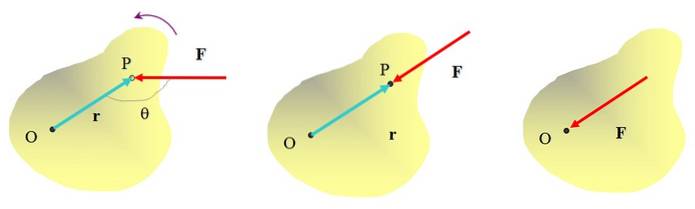
Å bruke kraft direkte på punkt O vil heller ikke snu objektet. Så det er klart at for å oppnå en rotasjonseffekt, må kraften påføres i en viss avstand fra rotasjonsaksen, og dens handlingslinje må ikke passere gjennom aksen..
Definisjon av dreiemoment
Dreiemomentet eller momentet til en kraft, betegnet som τ, vektorstørrelsen som er ansvarlig for å sette alle disse fakta sammen, er definert som:
τ = r x F
Vektoren r den er rettet fra rotasjonsaksen til kraftens påføringspunkt og deltakelsen av vinkelen mellom r og F er viktig. Derfor uttrykkes dreiemomentets størrelse som:
τ = r.F.sen hva
Det mest effektive dreiemomentet oppstår når r Y F de er vinkelrette.
Nå, hvis det er ønskelig at det ikke er noen rotasjoner eller disse skjer med konstant vinkelakselerasjon, er det nødvendig at summen av momentene som virker på objektet er null, analogt med det som ble vurdert for kreftene:
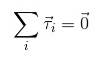
Likevektsforhold
Balanse betyr stabilitet, harmoni og balanse. For at et objekt skal bevege seg med disse egenskapene, må forholdene beskrevet i de foregående avsnittene brukes:
1) F1+ Fto + F3 +…. = 0
2) τ1+ τto + τ3 +…. = 0
Den første tilstanden garanterer translasjonell likevekt og den andre rotasjonsvekt. Begge må oppfylles hvis objektet skal forbli i statisk likevekt (fravær av bevegelse av noe slag).
applikasjoner
Likevektsforhold gjelder for mange strukturer, siden når bygninger eller forskjellige gjenstander bygges, gjøres det med den hensikt at delene deres forblir i samme relative posisjoner med hverandre. Med andre ord at objektet ikke demonteres.
Dette er viktig for eksempel når du bygger broer som forblir faste under føttene, eller når du designer beboelige strukturer som ikke endrer stilling eller har en tendens til å velte..
Selv om det antas at ensartet rettlinjet bevegelse er en ekstrem forenkling av bevegelse, som sjelden forekommer i naturen, må man huske at lysets hastighet i vakuum er konstant, og lyden i luften også hvis man anser mediet homogent..
I mange menneskeskapte mobile strukturer er det viktig at en konstant hastighet opprettholdes: for eksempel på rulletrapper og monteringslinjer.
Eksempler på translasjonell likevekt
Dette er den klassiske øvelsen av spenningene som holder lampen i balanse. Det er kjent at lampen veier 15 kg. Finn størrelsen på spenningene som er nødvendige for å holde den i denne posisjonen.
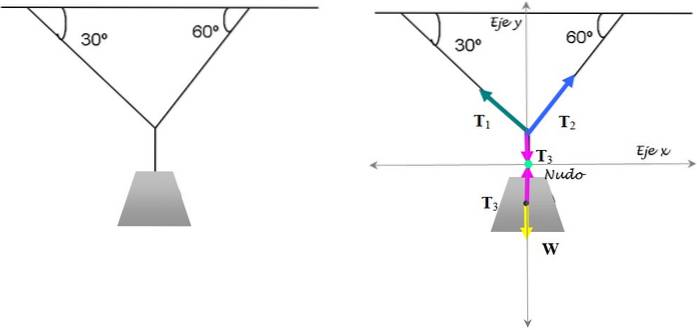
Løsning
For å løse det fokuserer vi på knuten der de tre strengene møtes. De respektive frikroppsdiagrammene for noden og lampen er vist i figuren ovenfor..
Vekten av lampen er W = 5 kg. 9,8 m / sto = 49 N. For at lampen skal være i likevekt, er det tilstrekkelig at den første likevektsbetingelsen er oppfylt:
T3 - W = 0
T3 = W = 49 N.
Spenninger T1 Y Tto må spaltes:
T1 år + T2 og - T3 = 0 (Sum av krefter langs y-aksen)
-T1x +T2x = 0 (Sum av krefter langs x-aksen)
Bruk av trigonometri:
T1.cos 60º + Tto .cos 30º = 49
- T1.sen60º + Tto.sin30º = 0
Det er et system med to ligninger med to ukjente, hvis svar er: T1 = 24,5 N Y Tto = 42,4 N.
Referanser
- Rex, A. 2011. Fundamentals of Physics. Pearson. 76 - 90.
- Serway, R., Jewett, J. (2008). Fysikk for naturvitenskap og ingeniørfag. Volum 1. 7ma. Ed. Cengage Learning. 120 - 124.
- Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9na Ed. Cengage Learning. 99-112.
- Tippens, P. 2011. Fysikk: Konsepter og applikasjoner. 7. utgave. MacGraw Hill. 71 - 87.
- Walker, J. 2010. Fysikk. Addison Wesley. 332 -346.



Ingen har kommentert denne artikkelen ennå.