
Prøvetakingsfeilformler og ligninger, beregning, eksempler
De prøvetakingsfeil eller prøvefeil I statistikk er det forskjellen mellom gjennomsnittsverdien til et utvalg og gjennomsnittsverdien til den totale befolkningen. For å illustrere ideen, la oss forestille oss at den totale befolkningen i en by er en million mennesker, hvorav den gjennomsnittlige skostørrelsen er ønsket, og det tas et tilfeldig utvalg på tusen mennesker..
Gjennomsnittsstørrelsen som kommer ut av prøven vil ikke nødvendigvis sammenfalle med den for den totale befolkningen, men hvis prøven ikke er partisk, må verdien være nær. Denne forskjellen mellom gjennomsnittsverdien av prøven og den totale befolkningen er prøvetakingsfeilen.
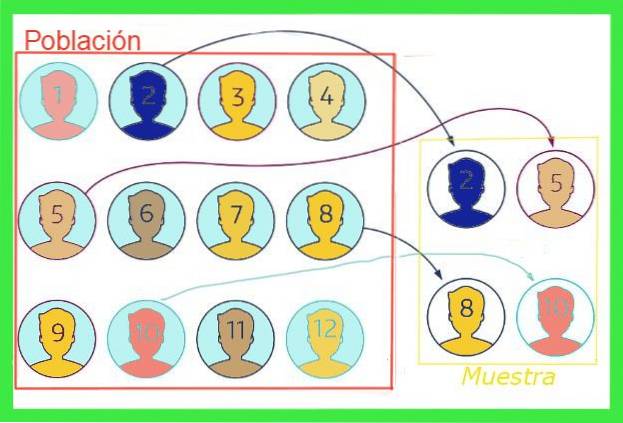
Generelt er middelverdien av den totale befolkningen ukjent, men det er teknikker for å redusere denne feilen og formler for å estimere prøvetakingsfeilmargin som vil bli eksponert i denne artikkelen.
Artikkelindeks
- 1 Formler og ligninger
- 2 Hvordan beregne prøvetakingsfeil
- 2.1 For et konfidensnivå γ
- 3 eksempler
- 3.1 - Eksempel 1
- 3.2 - Eksempel 2
- 3.3 - Eksempel 3
- 3.4 - Eksempel 4
- 3.5 - Øvelse 5
- 4 Referanser
Formler og ligninger
La oss si at du vil vite gjennomsnittsverdien til en viss målbar egenskap x i en befolkning av størrelse N, men hvordan N er et stort antall, er det ikke mulig å gjennomføre studien på den totale befolkningen, så fortsetter vi å ta en aleatory sample av størrelse n<
Gjennomsnittsverdien for prøven er betegnet med
Anta at de tar m prøver fra den totale befolkningen N, alle like store n med middelverdier
Disse middelverdiene vil ikke være identiske med hverandre, og vil alle være rundt befolkningens middelverdi μ. De prøvetakingsmargin E indikerer forventet separasjon av middelverdiene
De standard feilmargin ε størrelsesprøve n Det er:
ε = σ / √n
hvor σ er standardavviket (kvadratroten til variansen), som beregnes ved hjelp av følgende formel:
σ = √ [(x -
Meningen med standard feilmargin ε er følgende:
De middelverdi
Hvordan beregne prøvetakingsfeil
I forrige avsnitt ble formelen gitt for å finne feilområde standard av et utvalg av størrelse n, der ordet standard indikerer at det er en feilmargin med 68% konfidens.
Dette indikerer at hvis det ble tatt mange prøver av samme størrelse n, 68% av dem vil gi gjennomsnittsverdier
Det er en enkel regel, kalt regel 68-95-99.7 som lar oss finne margen på prøvetakingsfeil E for tillitsnivåer av 68%, 95% Y 99,7% lett, siden denne margen er 1⋅ε, 2⋅ε og 3⋅ε henholdsvis.
For et selvtillit γ
Hvis han konfidensnivå γ ikke er noe av det ovennevnte, så er prøvetakingsfeilen standardavviket σ multiplisert med faktoren Zγ, som oppnås gjennom følgende prosedyre:
1.- Først signifikansnivå α som beregnes fra konfidensnivå γ bruker følgende forhold: α = 1 - γ
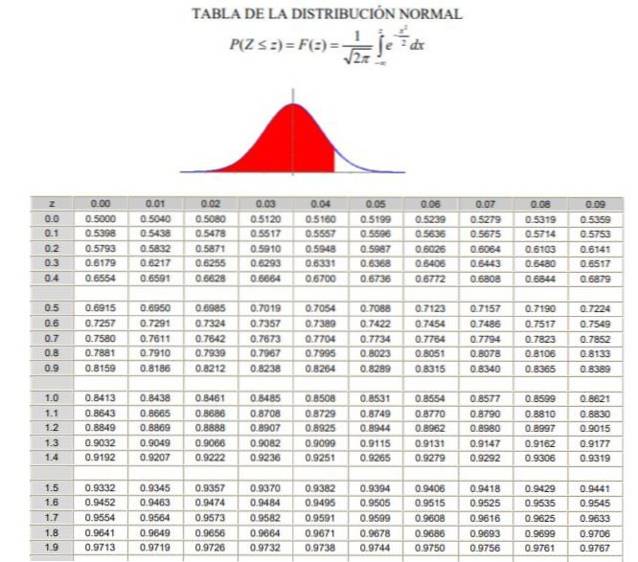
2.- Da må du beregne verdien 1 - α / 2 = (1 + γ) / 2, som tilsvarer den akkumulerte normale frekvensen mellom -∞ og Zγ, i en normal eller standardisert gaussisk fordeling F (z), hvis definisjon kan sees i figur 2.
3.- Ligningen er løst F (Zy) = 1 - α / 2 ved hjelp av tabellene for normalfordeling (kumulativ) F, eller ved hjelp av et dataprogram som har den omvendte standardiserte Gaussiske funksjonen F-1.
I sistnevnte tilfelle har vi:
Zγ = G-1(1 - α / 2).
4. - Til slutt brukes denne formelen for prøvetakingsfeilen med et pålitelighetsnivå γ:
E = Zγ⋅(σ / √n)
Eksempler
- Eksempel 1
Beregn standard feilmargin i gjennomsnittsvekten til et utvalg på 100 nyfødte. Beregningen av gjennomsnittsvekten var
Løsning
De standard feilmargin Det er ε = σ / √n = (1500 kg) / √100 = 0,15 kg. Hvilket betyr at med disse dataene kan det utledes at vekten på 68% av nyfødte er mellom 2950 kg og 3,25 kg.
- Eksempel 2
Fastslå marginen for prøvetakingsfeil E og vektområdet på 100 nyfødte med 95% konfidensnivå hvis gjennomsnittsvekten er 3100 kg med standardavvik σ = 1500 kg.
Løsning
Hvis den regel 68; 95; 99,7 → 1⋅ε; 2⋅ε; 3⋅ε, du har:
E = 2⋅ε = 2⋅0,15 kg = 0,30 kg
Det vil si at 95% av nyfødte vil ha vekter mellom 2800 kg og 3400 kg.
- Eksempel 3
Bestem vektområdet til de nyfødte fra eksempel 1 med en konfidensmargin på 99,7%.
Løsning
Prøvetakingsfeilen med 99,7% konfidens er 3 σ / √n, som for vårt eksempel er E = 3 * 0,15 kg = 0,45 kg. Herfra utledes det at 99,7% av nyfødte vil ha vekter mellom 2650 kg og 3550 kg.
- Eksempel 4
Bestem faktoren Zγ for et pålitelighetsnivå på 75%. Bestem marginen for prøvetakingsfeil med dette pålitelighetsnivået for saken presentert i eksempel 1.
Løsning
De selvtillitsnivå Det er γ = 75% = 0,75 som er relatert til Signifikansnivå α gjennom forhold γ= (1 - α), slik at signifikansnivået er α = 1 - 0,75 = 0,25.
Dette betyr at den kumulative normale sannsynligheten mellom -∞ og Zγ Det er:
P (Z ≤ Zγ ) = 1 - 0,125 = 0,875
Hva tilsvarer en verdi Zγ 1.1503, som vist i figur 3.
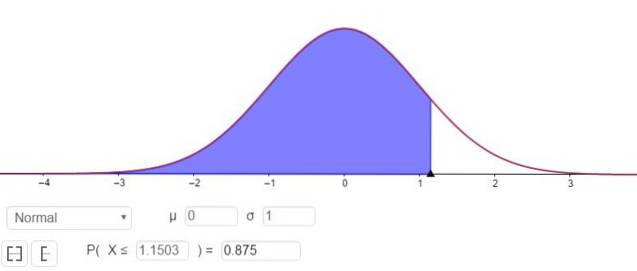
Det vil si at prøvetakingsfeilen er E = Zγ⋅(σ / √n)= 1.15⋅(σ / √n).
Når det brukes på dataene fra eksempel 1, gir det en feil på:
E = 1,15 * 0,15 kg = 0,17 kg
Med et konfidensnivå på 75%.
- Øvelse 5
Hva er konfidensnivået hvis Zα / 2 = 2,4 ?
Løsning
P (Z ≤ Zα / 2 ) = 1 - α / 2
P (Z ≤ 2,4) = 1 - α / 2 = 0,9918 → α / 2 = 1 - 0,9918 = 0,0082 → α = 0,0164
Betydningsnivået er:
α = 0,0164 = 1,64%
Og til slutt forblir tillitsnivået:
1- α = 1 - 0,0164 = 100% - 1,64% = 98,36%
Referanser
- Canavos, G. 1988. Sannsynlighet og statistikk: Applikasjoner og metoder. Mcgraw hill.
- Devore, J. 2012. Sannsynlighet og statistikk for ingeniørvitenskap og vitenskap. 8. plass. Utgave. Cengage.
- Levin, R. 1988. Statistikk for administratorer. 2. plass. Utgave. Prentice hall.
- Sudman, S. 1982. Still spørsmål: En praktisk guide til utforming av spørreskjema. San Fransisco. Jossey bass.
- Walpole, R. 2007. Sannsynlighet og statistikk for ingeniørfag og vitenskap. Pearson.
- Wonnacott, T.H. og R.J. Wonnacott. 1990. Innledende statistikk. 5. utgave Wiley
- Wikipedia. Prøvetakingsfeil. Gjenopprettet fra: en.wikipedia.com
- Wikipedia. Feilmargin. Gjenopprettet fra: en.wikipedia.com


Ingen har kommentert denne artikkelen ennå.