De volumstrøm det gjør det mulig å bestemme væskevolumet som passerer gjennom en seksjon av ledningen og tilveiebringe et mål på hastigheten som fluidet beveger seg gjennom. Derfor er målingen spesielt interessant innen så forskjellige felt som industri, medisin, konstruksjon og forskning, blant andre..
Imidlertid er det ikke så enkelt å måle hastigheten til en væske (det være seg en væske, en gass eller en blanding av begge) som å måle forskyvningshastigheten til et fast legeme. Derfor hender det at for å kjenne hastigheten til en væske er det nødvendig å kjenne dens strømning.
Dette og mange andre spørsmål knyttet til væske håndteres av grenen av fysikk kjent som væskemekanikk. Strømning er definert som hvor mye væske som passerer gjennom en seksjon av en kanal, det være seg en rørledning, en oljerørledning, en elv, en kanal, en blodledning, etc., med tanke på en tidsenhet.
Volumet som passerer gjennom et gitt område i en tidsenhet blir vanligvis beregnet, også kalt volumstrøm. Massen eller massestrømmen som passerer gjennom et gitt område på et bestemt tidspunkt er også definert, selv om den brukes sjeldnere enn volumstrøm..
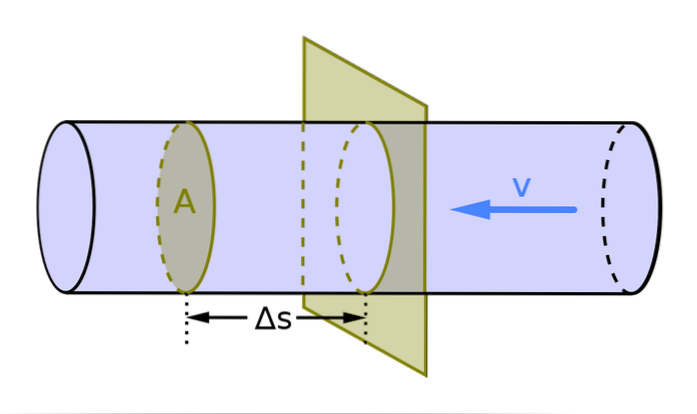
Den volumetriske strømningshastigheten er representert med bokstaven Q. For de tilfeller der strømmen beveger seg vinkelrett på lederseksjonen, bestemmes den med følgende formel:
Q = A = V / t
I denne formelen er A seksjonen av lederen (det er fluidets gjennomsnittshastighet), V er volumet og t er tiden. Siden i det internasjonale systemet måles arealet eller delen av lederen i mto og hastigheten i m / s måles strømningen m3/ s.
For de tilfellene hvor hastigheten til væskeforskyvningen skaper en vinkel θ med retningen vinkelrett på overflateseksjonen A, er uttrykket for å bestemme strømningshastigheten følgende:
Q = A cos θ
Dette er i samsvar med den forrige ligningen, siden strømmen er vinkelrett på området A, θ = 0 og derfor cos θ = 1.
Ovennevnte ligninger gjelder bare hvis væskens hastighet er jevn og hvis seksjonens område er flatt. Ellers beregnes volumstrømmen gjennom følgende integral:
Q = ∫∫s v d S
I denne integrerte dS er overflatevektoren, bestemt av følgende uttrykk:
dS = n dS
Der er n enhetsvektoren normal til kanaloverflaten og dS et overflatedifferensielt element.
Et kjennetegn ved ukomprimerbare væsker er at massen av væsken konserveres ved hjelp av to seksjoner. Av denne grunn er kontinuitetsligningen tilfredsstilt, som etablerer følgende forhold:
ρ1 TIL1 V1 = ρto TILto Vto
I denne ligningen er ρ væskens tetthet.
For tilfeller av regimer i permanent strømning, hvor tettheten er konstant, og det er derfor sant at ρ1 = ρto, koker ned til følgende uttrykk:
TIL1 V1 = Ato Vto
Dette tilsvarer bekreftelse av at strømmen er bevart, og derfor:
Spørsmål1 = Qto.
Av observasjonen av det ovennevnte følger at væske akselererer når de når en smalere del av en kanal, mens de bremser når de når en bredere del av en kanal. Dette faktum har interessante praktiske anvendelser, siden det gjør det mulig å spille med bevegelseshastigheten til en væske.
Bernoullis prinsipp bestemmer at for en ideell væske (det vil si en væske som verken har viskositet eller friksjon) som beveger seg i sirkulasjon gjennom en lukket ledning, forblir energien konstant gjennom hele forskyvningen..
Til syvende og sist er Bernoullis prinsipp ikke annet enn formuleringen av loven om bevaring av energi for strømmen av en væske. Dermed kan Bernoullis ligning formuleres som følger:
h + vto / 2g + P / ρg = konstant
I denne ligningen er h høyden og g er akselerasjonen på grunn av tyngdekraften.
Bernoulli-ligningen tar hensyn til energien til en væske når som helst, en energi som består av tre komponenter.
I dette tilfellet uttrykkes Bernoullis ligning som følger:
h ρ g + (vto ρ) / 2 + P = konstant
Logisk sett, når det gjelder en virkelig væske, oppfylles ikke uttrykket for Bernoulli-ligningen, siden friksjonstap oppstår i væskeforskyvningen, og det er nødvendig å ty til en mer kompleks ligning.
Volumstrøm vil bli påvirket hvis det er en hindring i kanalen.
I tillegg kan den volumetriske strømningshastigheten også endres på grunn av variasjoner i temperatur og trykk i den virkelige væsken som beveger seg gjennom en kanal, spesielt hvis dette er en gass, siden volumet som en gass opptar varierer som en funksjon av temperaturen og trykket på.
En veldig enkel metode for å måle volumstrøm er å la væske strømme inn i en doseringstank i en spesifisert tidsperiode..
Denne metoden er generelt ikke veldig praktisk, men sannheten er at det er ekstremt enkelt og veldig illustrerende å forstå betydningen og viktigheten av å kjenne strømningshastigheten til en væske..
På denne måten får fluidet strømme inn i en målebeholder i en periode, det akkumulerte volumet måles og det oppnådde resultatet deles med forløpt tid.
Ingen har kommentert denne artikkelen ennå.