
Transcendente funksjonstyper, definisjon, egenskaper, eksempler
De transcendente funksjoner Elementær er eksponentielle, logaritmiske, trigonometriske, inverse trigonometriske funksjoner, hyperbolsk og invers hyperbolsk. Det vil si at de er de som ikke kan uttrykkes ved hjelp av et polynom, et kvotient av polynomer eller røtter av polynomer..
De ikke-elementære transcendente funksjonene er også kjent som spesialfunksjoner, og blant dem kan feilfunksjonen navngis. De algebraiske funksjoner (polynomer, kvoter av polynomer og røtter av polynomer) sammen med transcendente funksjoner elementaler utgjør det som i matematikk er kjent som elementære funksjoner.
Transcendente funksjoner blir også betraktet som de som skyldes operasjoner mellom transcendente funksjoner eller mellom transcendente og algebraiske funksjoner. Disse operasjonene er: summen og forskjellen på funksjoner, produkt og kvotient av funksjoner, samt sammensetningen av to eller flere funksjoner.
Artikkelindeks
- 1 Definisjon og egenskaper
- 1.1 Eksponensiell funksjon
- 1.2 Egenskaper til den eksponensielle funksjonen
- 1.3 Logaritmisk funksjon
- 1.4 Egenskaper for logaritmefunksjonen
- 1.5 Sinus-, Cosine- og Tangent-funksjoner
- 2 Derivater og integraler
- 2.1 Derivat av den eksponensielle funksjonen
- 2.2 Integrering av den eksponensielle funksjonen
- 2.3 Tabell over derivater og integraler av transcendente funksjoner
- 3 eksempler
- 3.1 Eksempel 1
- 3.2 Eksempel 2
- 4 Referanser
Definisjon og egenskaper
Eksponensiell funksjon
Det er en reell funksjon av virkelig uavhengig variabel av skjemaet:
f (x) = a ^ x = ax
hvor til er et positivt reelt tall (a> 0) fast kalt basen. Omslagsfaget eller overskrift brukes til å betegne den potensierende operasjonen.
La oss si a = 2 så ser funksjonen slik ut:
f (x) = 2 ^ x = 2x
Som vil bli evaluert for flere verdier av den uavhengige variabelen x:

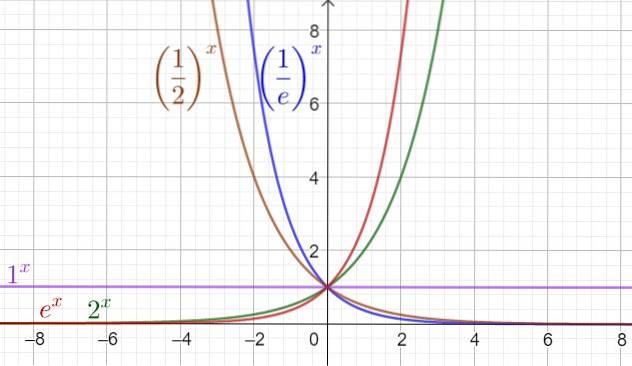
Nedenfor er en graf der den eksponensielle funksjonen er representert for forskjellige verdier av basen, inkludert basen og (Neper nummer og ≃ 2,72). Utgangspunkt og er så viktig at generelt når vi snakker om en eksponentiell funksjon vi tenker på e ^ x, som også er betegnet exp (x).

Egenskaper til den eksponensielle funksjonen
Fra figur 1 kan det sees at domenet til eksponensielle funksjoner er de reelle tallene (Dom f = R) og rekkevidden eller banen er de positive realene (Ran f = R+).
På den annen side, uavhengig av verdien til basen a, passerer alle eksponensielle funksjoner gjennom punktet (0, 1) og gjennom punktet (1, a).
Når basen a> 1, da øker funksjonen og når 0 < a < 1 funksjonen synker.
Kurver av y = a ^ x og av y = (1 / a) ^ x er symmetriske rundt aksen Y.
Bortsett fra saken a = 1, den eksponensielle funksjonen er injeksjonsdyktig, det vil si at hver verdi av bildet tilsvarer en og en startverdi.
Logaritmisk funksjon
Det er en reell funksjon av reell uavhengig variabel basert på definisjonen av logaritmen til et tall. Logaritmen som skal baseres til av et tall x, Det er tallet Y som basen må heves for å oppnå argumentet til x:
Loggtil(x) = y ⇔ a ^ y = x
Det er det logaritmefunksjon i basen til er den omvendte funksjonen til den eksponensielle funksjonen i basen til.
For eksempel:
Loggto1 = 0, siden 2 ^ 0 = 1
En annen sak, loggto4 = 2, fordi 2 ^ 2 = 4
Logaritmen til roten til 2 er loggto√2 = ½, fordi 2 ^ ½ = √2
Loggto ¼ = -2, siden 2 ^ (- 2) = ¼
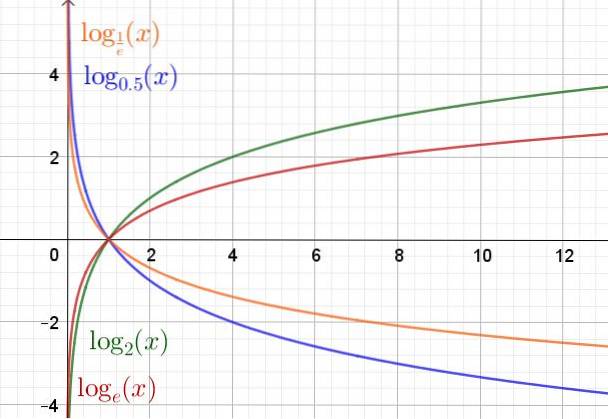
Nedenfor er en graf over logaritmefunksjonen i forskjellige baser.
Egenskaper for logaritmefunksjonen
Domenet til logaritmefunksjonen y (x) = loggtil(x) er de positive reelle tallene R+. Området eller området er de reelle tallene R.
Uavhengig av basen passerer logaritmefunksjonen alltid gjennom punktet (1,0) og punktet (a, 1) tilhører grafen til denne funksjonen.
I tilfelle at basen a er større enn enhet (a> 1) øker logaritmefunksjonen. Men hvis (0 < a < 1) entonces es una función decreciente.
Sinus, Cosine og Tangent Funksjoner
Sinusfunksjonen tilordner et reelt tall y til hver x-verdi, hvor x representerer mål for en vinkel i radianer. For å oppnå verdien av Sen (x) for en vinkel, er vinkelen representert i enhetssirkelen, og projiseringen av nevnte vinkel på den vertikale aksen er sinus som tilsvarer den vinkelen.
Følgende viser (i figur 3) trigonometrisk sirkel og sinus for forskjellige vinkelverdier X1, X2, X3 og X4.
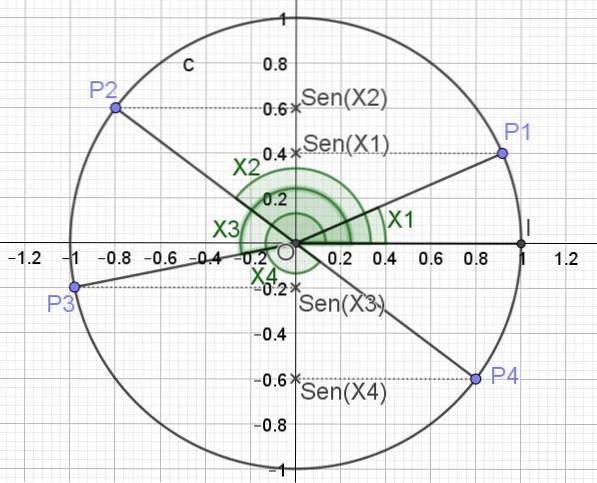
Definert på denne måten er maksimumsverdien funksjonen Sen (x) kan ha 1, som oppstår når x = π / 2 + 2π n, der n er et helt tall (0, ± 1, ± 2,). Minimumsverdien funksjonen Sen (x) kan ta oppstår når x = 3π / 2 + 2π n.
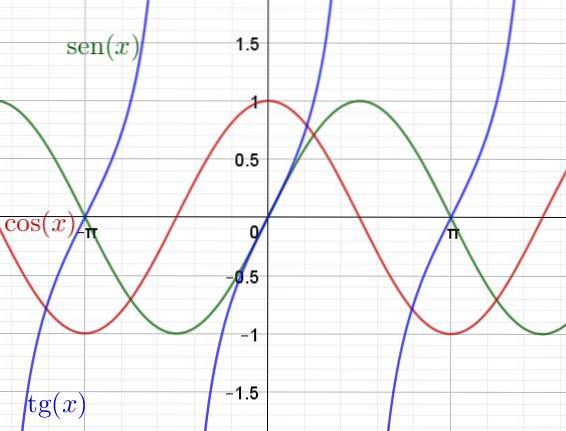
Kosinusfunksjonen y = Cos (x) er definert på en lignende måte, men projiseringen av vinkelposisjonene P1, P2, etc. utføres på den horisontale aksen til den trigonometriske sirkelen..
På den annen side er funksjonen y = Tan (x) kvotienten mellom sinusfunksjonen og cosinusfunksjonen.
Nedenfor er en graf over de transcendente funksjonene Sen (x), Cos (x) og Tan (x)
Derivater og integraler
Avledet av den eksponensielle funksjonen
Derivat Y ' av den eksponensielle funksjonen y = a ^ x er funksjonen a ^ x multiplisert med naturlig logaritme av base a:
y '= (a ^ x)' = a ^ x ln a
I det spesielle tilfellet med basen og, derivatet av den eksponensielle funksjonen er selve den eksponensielle funksjonen.
Integrert av den eksponensielle funksjonen
Den ubestemte integralen av a ^ x er selve funksjonen delt av den naturlige logaritmen til basen.
I det spesielle tilfellet av basen e er integriteten til den eksponensielle funksjonen den eksponensielle funksjonen i seg selv.
Tabell over derivater og integraler av transcendente funksjoner
Nedenfor er en oversiktstabell over de viktigste transcendente funksjonene, deres derivater og ubestemte integraler (antiderivativer):

Eksempler
Eksempel 1
Finn funksjonen som er resultatet av sammensetningen av funksjonen f (x) = x ^ 3 med funksjonen g (x) = cos (x):
(f eller g) (x) = f (g (x)) = cos3(x)
Dens derivat og dets ubestemte integral er:
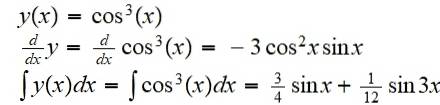
Eksempel 2
Finn sammensetningen av funksjonen g med funksjonen f, hvor g og f er funksjonene som er definert i forrige eksempel:
(g eller f) (x) = g (f (x)) = cos (x3)
Det skal bemerkes at sammensetningen av funksjoner ikke er en kommutativ operasjon.
Derivatet og den ubestemte integralen for denne funksjonen er henholdsvis:

Integralen ble igjen indikert fordi det ikke er mulig å skrive resultatet som en kombinasjon av elementære funksjoner nøyaktig.
Referanser
- Beregning av en enkelt variabel. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. nov 2008
- The Implicit Function Theorem: History, Theory, and Applications. Steven G. Krantz, Harold R. Parks. Springer Science & Business Media, 9. nov. 2012
- Multivariabel analyse. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. des. 2010
- Systemdynamikk: modellering, simulering og kontroll av mekatroniske systemer. Dekan C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. mars 2012
- Kalkulus: Matematikk og modellering. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1. jan 1999
- wikipedia. Transcendent funksjon. Gjenopprettet fra: es.wikipedia.com



Ingen har kommentert denne artikkelen ennå.