De inverse trigonometriske funksjoner, Som navnet antyder, er de de tilsvarende omvendte funksjonene til sinus-, cosinus-, tangent-, cotangent-, secant- og cosecant-funksjonene..
Inverse trigonometriske funksjoner er betegnet med samme navn som deres tilsvarende direkte trigonometriske funksjon pluss prefikset bue. Og dermed:
1.- arcsen (x) er den inverse trigonometriske funksjonen til funksjonen sen (x)
to.- arccos (x) er den inverse trigonometriske funksjonen til funksjonen cos (x)
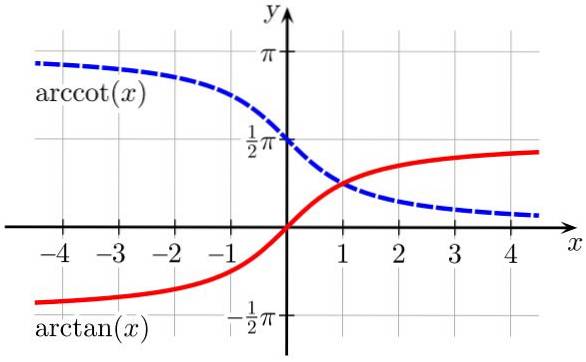
3.- arctan (x) er den inverse trigonometriske funksjonen til funksjonen så (x)
4.- arccot (x) er den inverse trigonometriske funksjonen til funksjonen barneseng (x)
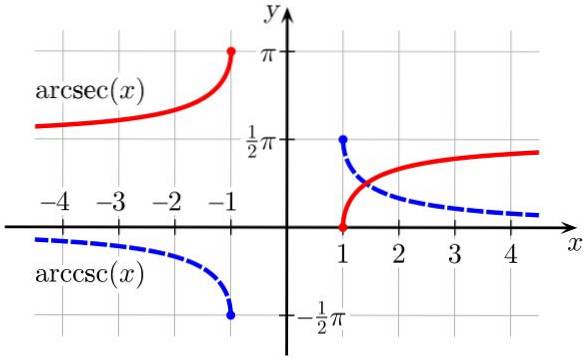
5.- buesek (x) er den inverse trigonometriske funksjonen til funksjonen sek (x)
6.- arccsc (x) er den inverse trigonometriske funksjonen til funksjonen csc (x)
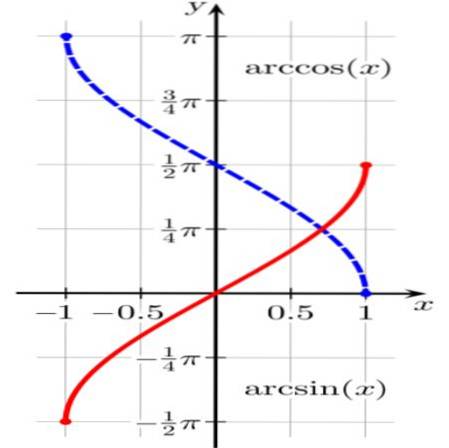
Funksjonen θ = lysbue (x) resulterer i en enhetsbue θ (eller vinkel i radianer θ) slik at sin (θ) = x.
Således er for eksempel lysbuen (√3 / 2) = π / 3 siden som kjent er sinusen til π / 3 radianer lik √3 / 2.
Artikkelindeks
For at en matematisk funksjon f (x) skal ha en invers g (x) = f-1(x) det er nødvendig at denne funksjonen er injeksjonsmiddel, som betyr at hver verdi y av ankomstsettet til funksjonen f (x) kommer fra en og bare én verdi x.
Det er klart at dette kravet ikke blir oppfylt av noen trigonometriske funksjoner. For å avklare poenget, merk at verdien y = 0,5 kan fås fra sinusfunksjonen på følgende måter:
Og mange flere, siden sinusfunksjonen er periodisk med periode 2π.
For å definere de inverse trigonometriske funksjonene, er det nødvendig å begrense domenet til deres tilsvarende direkte trigonometriske funksjoner, slik at de oppfyller injektivitetskravet.
Det begrensede domenet til den direkte funksjonen vil være området eller hovedgrenen til den tilsvarende inverse funksjonen.
For å oppnå derivatene av de inverse trigonometriske funksjonene, brukes egenskapene til derivatene, spesielt derivatet av en invers funksjon.
Hvis vi betegner med f (y) funksjonen og med f-1(x) til dens inverse funksjon, så er derivatet av den inverse funksjonen relatert til derivatet av den direkte funksjonen ved følgende forhold:
[F-1(x)] '= 1 / f' [f-1(x)]
For eksempel: hvis x = f (y) = √y er den direkte funksjonen, vil dens inverse være
y = f-1(x) = xto. La oss bruke regelen om avledet av det inverse i dette enkle tilfellet for å se at denne regelen faktisk oppfylles:
[xto] '= 1 / [√y]' = 1 / (½ y-½ = 2 og½ = 2 (xto)½ = 2x
Vel, vi kan bruke dette trikset for å finne derivatene av de inverse trigonometriske funksjonene.
For eksempel tar vi θ = lysbue (x) som den direkte funksjonen, vil dens inverse funksjon være sin (θ) = x.
[arcsen (x)] '= 1 / [sin (θ)]' = 1 / cos (θ) = 1 / √ (1 - sin (θ)to) = ...
… = 1 / √ (1 - xto) .
På denne måten kan alle derivater av de inverse trigonometriske funksjonene oppnås, som er vist nedenfor:
Disse derivatene er gyldige for ethvert argument z som tilhører de komplekse tallene, og derfor er de også gyldige for ethvert reelt argument x, siden z = x + 0i.
Finn arctan (1).
Arctan (1) er enhetsbuen (vinkel i radianer) ፀ slik at tan (ፀ) = 1. Den vinkelen er ፀ = π / 4 fordi tan (π / 4) = 1. Så arctan (1) = π / 4.
Beregn bue (cos (π / 3)).
Vinkelen π / 3 radianer er en bemerkelsesverdig vinkel hvis cosinus er ½, så problemet koker ned til å finne lysbuer (½).
Så er det et spørsmål om å finne hvilken vinkel hvis sinus gir ½. Den vinkelen er π / 6, siden sin (π / 6) = sin (30º) = ½. Derfor er arcsen (cos (π / 3)) = π / 6.
Finn resultatet av følgende uttrykk:
sek (arctan (3)) + csc (arccot (4))
Vi starter med å navngi α = arctan (3) og β = arccot (4). Så ser uttrykket vi må beregne slik ut:
sek (α) + csc (β)
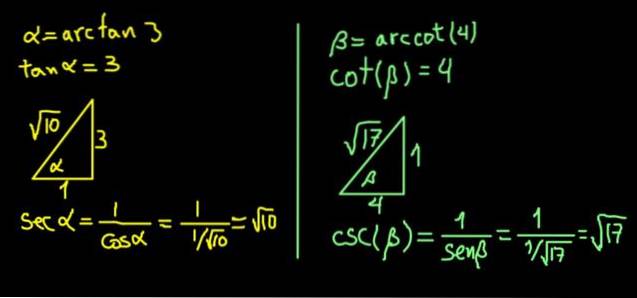
Uttrykket α = arctan (3) tilsvarer å si tan (α) = 3.
Siden tangenten er det motsatte benet over den tilstøtende, konstruerer vi en høyre trekant med benet motsatt α på 3 enheter og et tilstøtende ben på 1 enhet, slik at tan (α) = 3/1 = 3.
I en rett trekant bestemmes hypotenusen av Pythagoras teorem. Med disse verdiene er resultatet √10, slik at:
sek (α) = hypotenus / tilstøtende ben = √10 / 1 = √10.
Tilsvarende tilsvarer β = arccot (4) å bekrefte at barneseng (β) = 4.
Vi konstruerer en trekant med høyre ben ved siden av β på 4 enheter og et motsatt ben på 1 enhet, slik at barneseng (β) = 4/1.
Trekanten fullføres umiddelbart ved å finne hypotenusen takket være Pythagoras teorem. I dette tilfellet viste det seg å ha √17 enheter. Deretter beregnes csc (β) = hypotenuse / motsatt ben = √17 / 1 = √17.
Husk at uttrykket vi må beregne er:
sek (arctan (3)) + csc (arccot (4)) = sec (α) + csc (β) = ...
… = √10 + √17 = 3.16 + 4.12 = 7.28.
Finn løsningene til:
Cos (2x) = 1 - Sen (x)
Det er nødvendig at alle trigonometriske funksjoner uttrykkes i samme argument eller vinkel. Vi vil bruke identiteten til den dobbelte vinkelen:
Cos (2x) = 1-2 Sento(x)
Da reduseres det opprinnelige uttrykket til:
1 - 2 Sento(x) = 1 - Sen x
Når det er forenklet og tatt i betraktning, uttrykkes det som:
sin (x) (2 sin (x) - 1) = 0
Som gir opphav til to mulige ligninger: Sen (x) = 0 med løsning x = 0 og en annen ligning sin (x) = ½ med x = π / 6 som løsning.
Løsningene på ligningen er: x = 0 eller x = π / 6.
Finn løsningene til følgende trigonometriske ligning:
cos (x) = syndto(x)
For å løse denne ligningen er det praktisk å bare plassere en type trigonometrisk funksjon, så vi vil bruke den grunnleggende trigonometriske identiteten slik at den opprinnelige ligningen blir omskrevet som følger:
cos (x) = 1 - costo(x)
Hvis vi kaller y = cos (x), kan uttrykket skrives om som:
Yto + og - 1 = 0
Det er en ligning av andre grad i y, hvis løsninger er:
y = (-1 ± √5) / 2
Da er verdiene til x som tilfredsstiller den opprinnelige ligningen:
x = arccos ((-1 ± √5) / 2)
Den virkelige løsningen er den med et positivt tegn x = 0,9046 rad = 51,83º.
Den andre løsningen er kompleks: x = (π - 1.06 i) rad.
Ingen har kommentert denne artikkelen ennå.