
Analytisk geometri hvilke studier, historie, applikasjoner

De analytisk geometri studerer geometriske linjer og figurer ved å anvende grunnleggende teknikker for algebra og matematisk analyse i et gitt koordinatsystem.
Følgelig er analytisk geometri en gren av matematikken som analyserer i detalj alle dataene til geometriske figurer, det vil si volumet, vinklene, området, skjæringspunktene, deres avstander, blant andre..
Den grunnleggende egenskapen til analytisk geometri er at den tillater representasjon av geometriske figurer gjennom formler.
For eksempel er omkretsene representert av polynomligninger av andre grad, mens linjene uttrykkes av polynomligninger av første grad.
Analytisk geometri oppstår i det syttende århundre på grunn av behovet for å gi svar på problemer som til nå ikke hadde noen løsning. Den hadde som topprepresentanter René Descartes og Pierre de Fermat.
I dag peker mange forfattere på det som en revolusjonerende kreasjon i matematikkens historie, siden den representerer begynnelsen på moderne matematikk.
Artikkelindeks
- 1 Historie med analytisk geometri
- 1.1 Hovedrepresentanter for analytisk geometri
- 1.2 Pierre de Fermat
- 1.3 René Descartes
- 2 Grunnleggende elementer av analytisk geometri
- 2.1 Det kartesiske koordinatsystemet
- 2.2 Rektangulære koordinatsystemer
- 2.3 Polarkoordinatsystem
- 2.4 Kartesisk ligning av linjen
- 2.5 Rett linje
- 2.6 Kjegler
- 2.7 Omkrets
- 2.8 lignelse
- 2.9 Ellipse
- 2.10 Hyperbola
- 3 applikasjoner
- 3.1 Parabolantenn
- 3.2 Hengebroer
- 3.3 Astronomisk analyse
- 3.4 Cassegrain-teleskop
- 4 Referanser
Historie om analytisk geometri
Begrepet analytisk geometri oppstod i Frankrike i det syttende århundre på grunn av behovet for å gi svar på problemer som ikke kunne løses ved å bruke algebra og geometri isolert, men løsningen var i kombinert bruk av begge.
Hovedrepresentanter for analytisk geometri
I løpet av det syttende århundre utførte to franskmenn ved en tilfeldighet i livet forskning som på en eller annen måte endte i etableringen av analytisk geometri. Disse menneskene var Pierre de Fermat og René Descartes.
For tiden anses det at skaperen av analytisk geometri var René Descartes. Dette er på grunn av det faktum at han ga ut sin bok før Fermats og også i dybden med Descartes han tar for seg emnet analytisk geometri..
Imidlertid oppdaget både Fermat og Descartes at linjer og geometriske figurer kunne uttrykkes med ligninger og ligninger kunne uttrykkes som linjer eller geometriske figurer..
I følge oppdagelsene gjort av de to, kan det sies at begge er skaperne av analytisk geometri..
Pierre de Fermat
Pierre de Fermat var en fransk matematiker som ble født i 1601 og døde i 1665. I løpet av sitt liv studerte han geometrien til Euklid, Apollonius og Pappus, for å løse måleproblemene som eksisterte på den tiden.
Senere utløste disse studiene etableringen av geometri. De kom til uttrykk i boka hans "Introduksjon til flate og solide steder”(Ad Locos Planos et Solidos Isagoge), som ble utgitt 14 år etter hans død i 1679.
Pierre de Fermat anvendte i 1623 analytisk geometri på Apollonius 'teoremer på geometriske steder. Han var også den som først anvendte analytisk geometri i tredimensjonalt rom..
Rene Descartes
Også kjent som Cartesius, var han en matematiker, fysiker og filosof som ble født 31. mars 1596 i Frankrike og døde i 1650..
René Descartes publiserte i 1637 sin bok “Diskurs om metoden for å føre fornuft riktig og søke sannheten i vitenskapen"Bedre kjent som"Metoden”Og derfra ble begrepet analytisk geometri introdusert til verden. En av bilagene var "Geometrien".
Grunnleggende elementer i analytisk geometri
Analytisk geometri består av følgende elementer:
Det kartesiske koordinatsystemet
Dette systemet er oppkalt etter René Descartes.
Det var ikke han som kalte det, og heller ikke den som fullførte det kartesiske koordinatsystemet, men han var den som snakket om koordinater med positive tall som tillot fremtidige forskere å fullføre det..
Dette systemet består av det rektangulære koordinatsystemet og det polare koordinatsystemet.
Rektangulære koordinatsystemer
Rektangulære koordinatsystemer kalles planet dannet av omrisset av to tallinjer vinkelrett på hverandre, der avskjæringspunktet sammenfaller med felles null.
Da ville dette systemet bestå av en horisontal og en loddrett linje..
Den horisontale linjen er X-aksen eller abscissa-aksen. Den vertikale linjen vil være Y-aksen eller ordinataksen.
Polarkoordinatsystem
Dette systemet har ansvaret for å verifisere den relative posisjonen til et punkt i forhold til en fast linje og til et fast punkt på linjen.
Kartesisk ligning av linjen
Denne ligningen er hentet fra en linje når det er kjent to punkter som den passerer gjennom.
Rett linje
Det er en som ikke avviker og derfor verken har kurver eller vinkler.
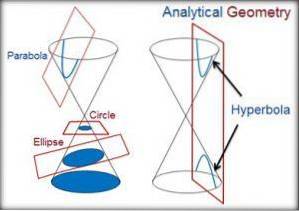
Kjegler
De er kurvene definert av linjene som går gjennom et fast punkt og av punktene i en kurve.
Ellipsen, omkretsen, parabolen og hyperbola er koniske kurver. Hver av dem er beskrevet nedenfor.
Omkrets
Omkrets kalles lukket plankurve som dannes av alle punktene i planet som er like langt fra et indre punkt, det vil si fra sentrum av omkretsen.
Lignelse
Det er stedet for punktene i planet som er like langt fra et fast punkt (fokus) og en fast linje (directrix). Deretter er directrix og fokus det som definerer parabolen.
Parabolen kan fås som et snitt av en konisk revolusjonsflate gjennom et plan parallelt med en generatrix.
Ellipse
En ellips er den lukkede kurven som beskriver et punkt når man beveger seg i et plan på en slik måte at summen av avstandene til to (2) faste punkter (kalt foci) er konstant.
Hyperbola
Kurven definert som punktet til punktene i planet kalles en hyperbola, for hvilken forskjellen mellom avstandene til to faste punkter (foci) er konstant..
Hyperbola har en symmetriakse som går gjennom foci, kalt fokalaksen. Den har også en annen som er deleskåret i segmentet som har de faste punktene i endene..
applikasjoner
Det er forskjellige anvendelser av analytisk geometri i forskjellige områder av dagliglivet. For eksempel kan vi finne parabolen, et av de grunnleggende elementene i analytisk geometri, i mange av verktøyene som brukes daglig i dag. Noen av disse verktøyene er følgende:
Parabolantenne
Parabolantenner har en reflektor generert som et resultat av en parabel som roterer på aksen til antennen. Overflaten som genereres som et resultat av denne handlingen kalles en paraboloid.
Denne evnen til paraboloid kalles den optiske egenskapen eller refleksjonsegenskapen til en parabel, og takket være dette er det mulig for paraboloidet å reflektere de elektromagnetiske bølgene den mottar fra matemekanismen som utgjør antennen..
Hengende broer
Når et tau støtter en vekt som er homogen, men som samtidig er betydelig større enn selve tauet, blir resultatet en parabel.
Dette prinsippet er grunnleggende for bygging av hengebroer, som vanligvis støttes av brede stålkabelkonstruksjoner..
Prinsippet om parabolen i hengebroer har blitt brukt i strukturer som Golden Gate Bridge, som ligger i byen San Francisco, i USA, eller den store broen i Akashi-stredet, som ligger i Japan og forbinder Øya Awaji med Honshū, hovedøya i landet.
Astronomisk analyse
Analytisk geometri har også hatt veldig spesifikke og avgjørende bruksområder innen astronomi. I dette tilfellet er elementet av analytisk geometri som er midtpunktet ellipsen; Johannes Keplers bevegelseslov av planetene er en refleksjon av dette.
Kepler, en tysk matematiker og astronom, bestemte at ellipsen var kurven som best passet Mars 'bevegelse; Han hadde tidligere prøvd den sirkulære modellen som var foreslått av Copernicus, men midt i eksperimentene hans utledet han at ellipsen tjente til å tegne en bane som var helt lik planeten han studerte..
Takket være ellipsen var Kepler i stand til å bekrefte at planetene beveget seg i elliptiske baner; dette hensynet var uttalelsen til den såkalte andre loven til Kepler.
Fra denne oppdagelsen, senere beriket av den engelske fysikeren og matematikeren Isaac Newton, var det mulig å studere planetens orbitasjonsbevegelser og øke kunnskapen vi hadde om universet som vi er en del av.
Cassegrain-teleskop
Cassegrain-teleskopet er oppkalt etter oppfinneren, den franskfødte fysikeren Laurent Cassegrain. I dette teleskopet brukes prinsippene for analytisk geometri fordi den hovedsakelig består av to speil: den første er konkav og parabolsk, og den andre er preget av å være konveks og hyperbolsk..
Plasseringen og naturen til disse speilene gjør at defekten kjent som sfærisk aberrasjon ikke kan finne sted. denne feilen forhindrer at lysstråler reflekteres i fokuset til en gitt linse.
Cassegrain-teleskopet er veldig nyttig for planetobservasjon, i tillegg til å være ganske allsidig og enkel å bruke..
Referanser
- Analytisk geometri. Hentet 20. oktober 2017 fra britannica.com
- Analytisk geometri. Hentet 20. oktober 2017 fra encyclopediafmath.org
- Analytisk geometri. Hentet 20. oktober 2017 fra khancademy.org
- Analytisk geometri. Hentet 20. oktober 2017 fra wikipedia.org
- Analytisk geometri. Hentet 20. oktober 2017 fra whitman.edu
- Analytisk geometri. Hentet 20. oktober 2017 fra stewartcalculus.com
- Flyanalytisk geometri Hentet 20. oktober 2017



Ingen har kommentert denne artikkelen ennå.