De homoscedasticity i en prediktiv statistisk modell oppstår det at i alle datagruppene til en eller flere observasjoner, variansen til modellen med hensyn til de forklarende (eller uavhengige) variablene forblir konstant.
En regresjonsmodell kan være homoscedastisk eller ikke, i så fall snakker vi om heteroscedasticity.
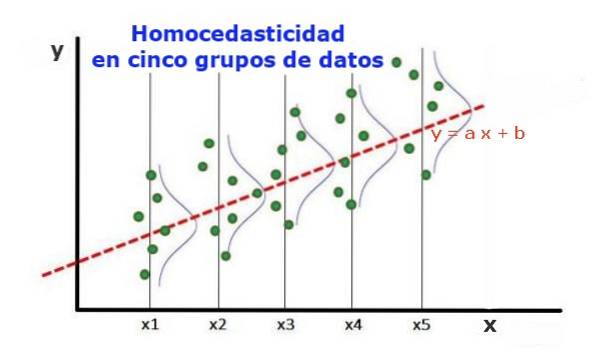
En statistisk regresjonsmodell av flere uavhengige variabler kalles homoscedastisk, bare hvis variansen til feilen til den forutsagte variabelen (eller standardavviket til den avhengige variabelen) forblir enhetlig for forskjellige gruppeverdier av de forklarende eller uavhengige variablene.
I de fem datagruppene i figur 1 er avviket i hver gruppe beregnet, med hensyn til verdien estimert av regresjonen, noe som resulterer i å være den samme i hver gruppe. Det antas videre at dataene følger normalfordelingen.
På det grafiske nivået betyr det at punktene er like spredt eller spredt rundt verdien som er forutsagt av regresjonspassformen, og at regresjonsmodellen har samme feil og gyldighet for området til den forklarende variabelen..
Artikkelindeks
For å illustrere viktigheten av homoscedasticity i prediktiv statistikk, er det nødvendig å kontrastere med det motsatte fenomenet, heteroscedasticity.
I tilfelle av figur 1, der det er homoscedasticity, er det sant at:
Var ((y1-Y1); X1) ≈ Var ((y2-Y2); X2) ≈… Var ((y4-Y4); X4)
Der Var ((yi-Yi); Xi) representerer variansen, representerer paret (xi, yi) data fra gruppe i, mens Yi er verdien som regnes for regresjonen for gjennomsnittsverdien Xi for gruppen. Variansen til n-dataene fra gruppe i beregnes som følger:
Var ((yi-Yi); Xi) = ∑j (yij - Yi) ^ 2 / n
Tvert imot, når heteroscedastisitet oppstår, kan det hende at regresjonsmodellen ikke er gyldig for hele regionen der den ble beregnet. Figur 2 viser et eksempel på denne situasjonen.
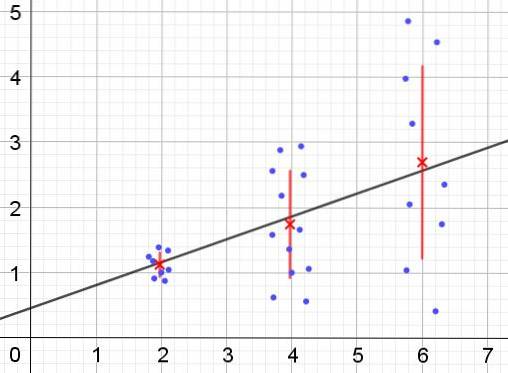
Figur 2 representerer tre grupper av data og passformen til settet ved hjelp av en lineær regresjon. Det skal bemerkes at dataene i den andre og tredje gruppen er mer spredt enn i den første gruppen. Grafen i figur 2 viser også gjennomsnittsverdien for hver gruppe og dens feilfelt ± σ, med σ standardavvik for hver datagruppe. Det skal huskes at standardavviket σ er kvadratroten til variansen.
Det er klart at når det gjelder heteroscedastisitet, endres regresjonsestimasjonsfeilen i verdiområdet til den forklarende eller uavhengige variabelen, og i intervallene der denne feilen er veldig stor, er regresjonsforutsigelsen upålitelig eller ikke anvendelig.
I en regresjonsmodell må feilene eller restene (og -Y) fordeles med lik varians (σ ^ 2) gjennom verdiområdet til den uavhengige variabelen. Det er av denne grunn at en god regresjonsmodell (lineær eller ikke-lineær) må bestå homoscedasticitetstesten..
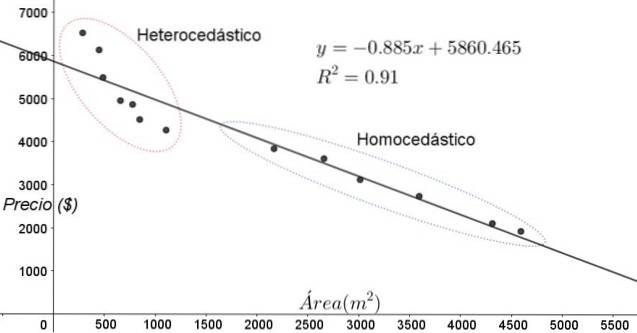
Punktene vist i figur 3 tilsvarer dataene fra en studie som ser etter et forhold mellom husprisene (i dollar) som en funksjon av størrelsen eller arealet i kvadratmeter..
Den første modellen som skal testes er en lineær regresjon. For det første bemerkes det at bestemmelseskoeffisienten R ^ 2 for tilpasningen er ganske høy (91%), så det kan tenkes at tilpasningen er tilfredsstillende..
Imidlertid kan to regioner skilles tydelig fra justeringsgrafen. En av dem, den til høyre innesluttet i en oval, oppfyller homoscedasticity, mens regionen til venstre ikke har homoscedasticity.
Dette betyr at prediksjonen til regresjonsmodellen er tilstrekkelig og pålitelig i området mellom 1800 m ^ 2 til 4800 m ^ 2, men veldig utilstrekkelig utenfor denne regionen. I den heteroscedastiske sonen er ikke bare feilen veldig stor, men også dataene ser ut til å følge en annen trend enn den som er foreslått av den lineære regresjonsmodellen..
Spredningsdiagrammet for dataene er den enkleste og mest visuelle testen av deres homoscedasticitet, men ved anledninger der det ikke er så tydelig som i eksemplet vist i figur 3, er det nødvendig å ty til grafer med hjelpevariabler..
For å skille områdene der homoscedasticitet er oppfylt og der den ikke er, introduseres de standardiserte variablene ZRes og ZPred:
ZRes = Abs (y - Y) / σ
ZPred = Y / σ
Det skal bemerkes at disse variablene avhenger av den anvendte regresjonsmodellen, siden Y er verdien av regresjonsforutsigelsen. Nedenfor er spredningsplottet ZRes vs ZPred for samme eksempel:
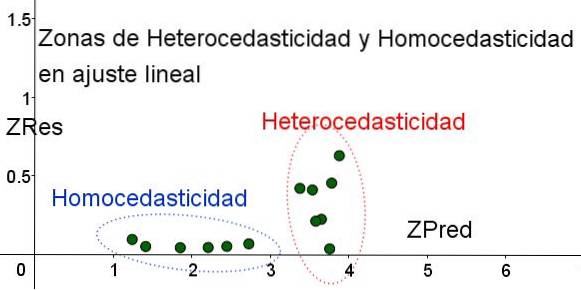
I grafen i figur 4 med standardiserte variabler er området der den gjenværende feilen er liten og ensartet, skilt tydelig fra området der den ikke er. I den første sonen oppfylles homoscedasticity mens i regionen der restfeilen er svært variabel og stor, oppfylles heteroscedasticity..
Regresjonsjustering blir brukt på samme gruppe data i figur 3, i dette tilfellet er justeringen ikke-lineær, siden modellen som brukes innebærer en potensiell funksjon. Resultatet er vist i følgende figur:
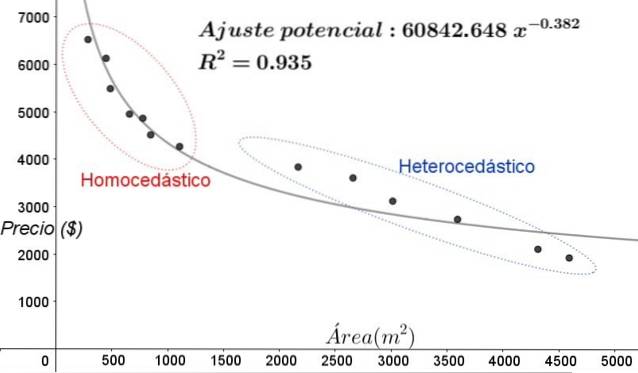
I grafen i figur 5 bør homoscedastiske og heteroscedastiske soner være tydelig bemerket. Det skal også bemerkes at disse sonene ble byttet ut med hensyn til de som ble dannet i modellen med lineær passform.
I grafen i figur 5 er det tydelig at selv når det er en ganske høy bestemmelseskoeffisient for passformen (93,5%), er ikke modellen tilstrekkelig for hele intervallet for den forklarende variabelen, siden dataene for verdier større enn 2000 m ^ 2 nåværende heteroscedasticity.
En av de ikke-grafiske testene som er mest brukt for å verifisere om homoscedasticity er oppfylt eller ikke, er Breusch-Pagan test.
Ikke alle detaljene i denne testen vil bli gitt i denne artikkelen, men dens grunnleggende egenskaper og trinnene i den er skissert i store trekk:
De fleste av de statistiske programvarepakkene som: SPSS, MiniTab, R, Python Pandas, SAS, StatGraphic og flere andre inkluderer homoscedasticity-testen av Breusch-Pagan. En annen test for å verifisere ensartethet av varians Levene-test.
Ingen har kommentert denne artikkelen ennå.