Trigonometriske identiteter (eksempler og øvelser)

De trigonometriske identiteter er forhold mellom trigonometriske forhold, som er sanne for enhver verdi av variabelen. For eksempel:

tan θ = sin θ / cos θ

Det er en trigonometrisk identitet som relaterer tre forhold mellom vinkelen θ, tangenten, sinusen og cosinusen til nevnte vinkel.

Denne identiteten gjelder for alle verdier, bortsett fra de som gjør 0 til nevneren. Cos θ er 0 for θ = ± π / 2, ± 3π / 2, ± 5π / 2 ... Et annet eksempel på trigonometrisk identitet er:

synd x. sek x. ctg x = 1

Artikkelindeks

• 1 Demo
• 2 Typer av trigonometriske identiteter
  • 2.1 - Grunnleggende trigonometriske identiteter
  • 2.2 - Pythagoras identiteter
  • 2.3 - Formler for cosinus og sinus for addisjon / subtraksjon av vinkler
  • 2.4 - Formler for dobbel vinkel
  • 2.5 - Formler for halvvinkelen
• 3 Løst øvelser
  • 3.1 - Øvelse 1
  • 3.2 - Øvelse 2
• 4 Referanser

Demonstrasjon

Det er to grunnleggende måter å vise at en trigonometrisk identitet er sann:

1 - Transformere et av medlemmene av likheten til det andre gjennom praktiske algebraiske manipulasjoner.

2- Utvikle begge medlemmene av likheten hver for seg, til de respektive endelige uttrykkene for hver enkelt er nøyaktig de samme.

I den foreslåtte identiteten skal vi transformere venstre side av likheten, som vi uttrykker ctg x og sec x for sinus og cosinus som følger:

ctg x = cos x / sin x

sek x = 1 / cos x

Vi erstatter dette uttrykket på venstre side av identiteten og forenkler:

synd x. (1 / cos x). (cos x / sin x) = (sin x. cos x / cos x. sin x) = 1

Og sannheten til identiteten er allerede bekreftet.

Typer av trigonometriske identiteter

Det er flere klasser av trigonometriske identiteter. Vi vil kort beskrive de viktigste nedenfor:

- Fundamentale trigonometriske identiteter

Vi skiller mellom to typer grunnleggende identiteter:

I) De som uttrykkes gjennom grunnforholdene sinus, cosinus og tangens:

• sek x = 1 / cos x
• cosec x / 1 / sin x
• ctg x = 1 / tg x
• tg x = sin x / cos x
• ctg x = cos x / sin x

II) De som kommer fra paritet. Vi vet fra grafen at sin x er en merkelig funksjon, noe som betyr at:

sin (-x) = - sin x

For sin del er cos x en jevn funksjon, derfor:

cos (-x) = cos x

Deretter:

tg (-x) = sin (-x) / cos (-x) = -sen x / cos x

På samme måte:

• cotg (-x) = -ctg x
• sek (-x) = sek x
• cosec (-x) = - cosec x

- Pythagoras identiteter

De er oppnådd ved anvendelse av Pythagoras teorem på høyre trekant av ben a og b og hypotenuse c. La oss se:

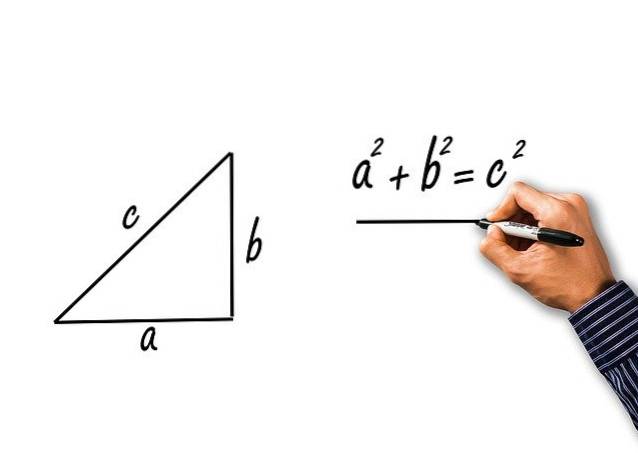
The Pythagorean teorem sier at:

c^to = a^to + b^to

Dele alt av c^to:

c^to / c^to = (a^to / c^to) + (B^to / c^to)

Begrepet til venstre er 1 og husker at sinus og cosinus i den spisse vinkelen α er definert som:

sin α = a / c

cos α = b / c

Resultat:

1 = (sin α)^to + (cos α)^to

Denne identiteten er kjent som grunnleggende identitet.

Prosedyren kan utføres ved å dele med a^to og b^to, som gir opphav til to flere identiteter:

sek^to α = 1 + tg^to α

innhøsting^to α = 1 + ctg^to α

- Formler for cosinus og sinus for tillegg / subtraksjon av vinkler

De viktigste trigonometriske identitetene for cosinus, sinus og tangens for addisjon og subtraksjon er som følger:

Bevis for synd (α + β) og cos (α + β)

Disse identitetene kan bevises geometrisk eller også ved Eulers formel:

og^iα = cos α + i sin α

La oss se hva som skjer med formelen når vi erstatter summen av to vinkler α og β:

og^{i (α +β)} = cos (α + β) + i sin (α + β)

Dette uttrykket er komplekst, dets virkelige del er cos (α + β) og dens imaginære del er i sin (α + β). Vi lagrer dette resultatet for senere bruk og fokuserer på å utvikle den eksponentielle delen:

og^{i (α +β)} = e^iα ⋅ e^iβ = (cos α + i sin α). (cos β + i sin β) =

= cos α⋅cos β + cos α⋅i sin β + i⋅sen α cos β - sin α⋅sen β

Den virkelige delen av dette uttrykket er den som ikke multipliseres med den tenkte enheten "i":

cos α⋅cos β - sin α. sin β

Den imaginære delen er derfor:

i (cos α⋅sen β + sin α⋅cos β)

For at to komplekse uttrykk skal være like, må den virkelige delen av den ene være den virkelige delen av den andre. Det samme skjer med imaginære deler.

Vi tar det lagrede resultatet og sammenligner det med dette:

cos α. cos β - sin α. sin β = cos (α + β)

i (cos α⋅sen β + sin α⋅cos β) = i sin (α + β)

sin (α + β) = (cos α. sin β + sin α⋅cos β)

- Formler for dobbel vinkel

I de forrige formlene tar vi β = α og utvikler:

sin (α + α) = sin 2 α = sin α⋅cos α + cos α. sin α = 2⋅ sin α ⋅ cos α

cos (α + α) = cos 2 α = cos α⋅cos α - sin α⋅sen α = cos^to α - synd ^to α

tg (α + α) = tg 2 α = [tg α + tg α] / [1- tg α⋅tg α] = 2tg α / 1- tg^to α

Hvis vi i det andre uttrykket erstatter cos^to α = 1 - synd^to α oppnås:

cos 2 α = cos^to α - (1- cos^to α) = 2 cos^to α -1

- Formler for halvvinkelen

I dette siste uttrykket, la oss erstatte α med α / 2, forblir følgende:

cos α = 2 cos ^to(α / 2) -1

Løser for:

Løst øvelser

- Øvelse 1

Vis det:

Vi skal jobbe venstre begrep algebraisk slik at det ser ut som det rette. Siden sin x vises i riktig begrep, er det første trinnet å uttrykke cos^tox når det gjelder sin x slik at alt er i samme trigonometriske forhold:

Da blir 1 - synd tatt med^to x fordi det er en forskjell på perfekte firkanter. For å gjøre dette, rydder det den grunnleggende identiteten:

cos^tox = 1 - synd^to x

1 - sen^to x = (1- sin x) (1 + sinx)

Og faktoriseringen er erstattet i det opprinnelige uttrykket:

Begrepet (1-sinx) er forenklet og en likhet er fortsatt:

1 + sin x = 1 + sinx

- Øvelse 2

Løs følgende trigonometriske ligning og gi løsningen for verdier mellom 0 og 360º:

tg x + sek^to x = 3

Løsning

I begrepet til venstre er det to trigonometriske forhold, derfor er det nødvendig å redusere alt til en enkelt, for å kunne løse det ukjente. Begrepet sek^to x uttrykkes gjennom en av de pytagoreiske identitetene:

sek^to α = 1 + tg^to α

Bytte i ligningen gjenstår:

tg x + 1 + tg^to x = 3

Omorganisere vilkårene:

tg^to x + tg x + 1 = 3

Denne ligningen løses ved å gjøre endringen av variabelen:

tg x = u

eller^to + u + 1 - 3 = 0 → u^to + u - 2 = 0

Denne kvadratiske ligningen løses enkelt ved å faktorisere:

(u +2) (u-1) = 0

Derfor u₁ = -2 og u_to = 1, som tilsvarer:

tg x₁ = -2

tg x_to = 1

Endelig:

x₁ = arctg (-2) = 296,6º

x_to  = arctg (1) = 45º

Referanser

1. Carena, M. 2019. Pre-University Mathematics Manual. National University of the Litoral.
2. Figuera, J. 1999. Matematikk. Første. Diversifisert. Bolivarian Collegiate Editions.
3. Hoffman, J. Selection of Mathematics Topics. Volum 4.
4. Jiménez, R. 2008. Algebra. Prentice hall.
5. Wikipedia. Trigonometri identiteter og formler. Gjenopprettet fra: es.wikipedia.org.
6. Zapata, F. 4 måter å løse en kvadratisk ligning på. Gjenopprettet fra: francesphysics.blogspot.com.
7. Zill, D. 1984. Algebra og trigonometri. Mcgraw hill.