
Ampères lovformel og ligninger, bevis, øvelser
De Ampères lov sier at sirkulasjonen av den magnetiske induksjonsvektoren B er proporsjonal med intensiteten I av strømmen som strømmer gjennom den.
I sin tur sirkulasjonen av B er summen av alle produktene mellom den tangentielle komponenten B║ og lengden på et lite segment Δℓ av en lukket kurve C, rundt en krets. I matematiske termer er det skrevet slik:
∑ B║ .Δℓ ∝ Jeg
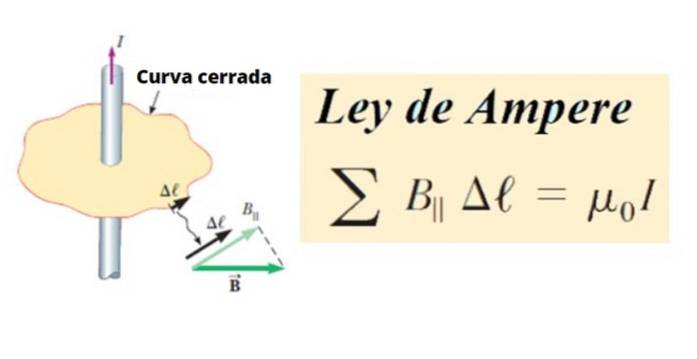
Som en vilkårlig linje eller kurve C, kan den deles inn i små segmenter Δℓ, og disse kan igjen være uendelige, da kalles de dℓ.
I dette tilfellet blir summeringen en linjeintegral av det skalære produktet mellom vektorene B og ds. Nevnte produkt inneholder tangensiell komponent av B, som er B cosθ, hvor θ er vinkelen mellom vektorene:
Den lille sirkelen gjennom integralen betyr at integrasjonen skjer over en lukket bane C, som i dette tilfellet involverer strømmen som strømmer gjennom tverrsnittet av lederen.
Konstanten av proporsjonalitet som er nødvendig for å etablere likhet er μeller, vakuumets permeabilitet. På denne måten er Ampères lov:

Ampères lov forteller oss at linjen integrert ∫C B ∙ ds er nøyaktig μellerJeg, men det gir oss ikke detaljene om hvordan magnetfeltet er orientert B med hensyn til kurve C ved hvert punkt, og heller ikke hvordan integralet skal beregnes. Det forteller oss bare at resultatet av det alltid er μellerJeg.
Artikkelindeks
- 1 Bevis på Ampères lov
- 1.1 Magnetfelt av rettlinjet og uendelig ledning
- 2 Løst øvelser
- 2.1 - Øvelse 1
- 2.2 - Øvelse 2
- 3 Referanser
Demonstrasjon av Ampères lov
Ampères lov blir verifisert eksperimentelt ved å kontrollere magnetfeltet produsert av en veldig lang rettlinjet leder. Før vi takler problemet, må vi trekke frem to tilfeller av spesiell interesse i den forrige ligningen:
-Den første er når B og ds er parallelle, noe som betyr at B er tangensiell for C. Da er vinkelen mellom begge vektorer 0º og skalarproduktet er ganske enkelt produktet av størrelsene B.ds.
-Det andre skjer hvis B og ds er vinkelrette, i hvilket tilfelle skalarproduktet er 0, siden vinkelen mellom vektorene er 90º, hvis cosinus er 0.
En annen viktig detalj er valget av kurve C som feltsirkulasjonen blir evaluert på. Ampères lov spesifiserer ikke hva det kan være, men det må innebære nåværende fordeling. Det står heller ikke i hvilken retning kurven skal kjøres, og det er to muligheter for dette.
Løsningen er å tildele tegn i henhold til regelen til høyre tommel. De fire fingrene er buet i retningen du vil integrere, vanligvis vil dette være det samme som feltet B sirkulere. Hvis strømmen peker i retning av høyre tommel, tildeles den et + tegn og hvis ikke et tegn -.
Dette gjelder når det er en fordeling med flere strømmer, noen kan være positive og noen negative. Den algebraiske summen av dem er den vi skal plassere i Ampères lov, som vanligvis kalles som gjeldende låst (etter kurve C).
Uendelig rettlinjet magnetisk felt
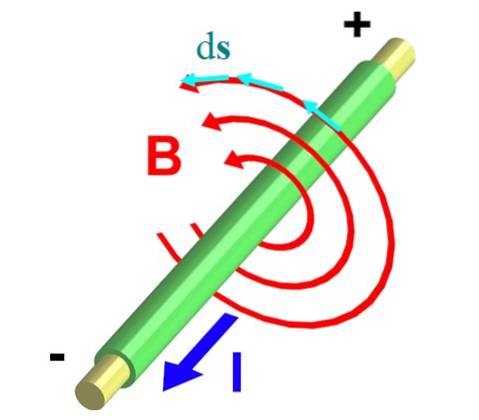
Figur 2 viser en ledning som bærer en strøm I ut av planet. Regelen om høyre tommel sørger for det B sirkulerer mot klokken, og beskriver omkretser som vist med de røde pilene.

La oss ta en av dem, hvis radius er r. Vi deler den opp i små differensielle segmenter ds, representert av vektorene i blått. Begge vektorene, B og ds, er parallelle på hvert punkt på omkretsen, og dermed integralet ∫C B ∙ ds Det forvandles til:
∫C Bds
Dette er fordi, som vi sa tidligere, prikkproduktet B ∙ ds er produktet av størrelsen på vektorene ved cosinus på 0º. Vi kjenner resultatet av integralen takket være Ampères lov, derfor skriver vi:
∫C Bds = μellerJeg
Siden feltets størrelse er konstant over hele banen, etterlater den integralen:
B ∫C ds = μellerJeg
Integralet ∫C ds representerer summen av alle uendelige segmenter som utgjør radiusens omkrets r, tilsvarer lengden, produktet av radien med 2π:
B.2πr = μellerJeg
Og derfra finner vi at størrelsen på B er:
B = μellerI / 2πr
Det bør understrekes at selv om den valgte banen (eller ampere-krets) var ikke sirkulær, resultatet av integralen forblir μellerJeg derimot ∫C B ∙ ds det ville det ikke lenger være B.2πr.
Derfor ligger nytten av Ampères lov for å bestemme magnetfeltet i å velge fordelinger med høy symmetri, slik at integralet er enkelt å evaluere. Sirkulære og rettlinjede stier oppfyller dette kravet.
Løst øvelser
- Øvelse 1
Tenk på kurvene a, b, c og d vist i figur 3. De involverer tre strømmer, to forlater planet, symbolisert med et punkt ( . ), hvis intensitet er 1 A og 5 A, og en strøm som kommer inn i planet, som er betegnet med et kors og hvis størrelse er 2 A.
Finn gjeldende vedlagt av hver kurve.
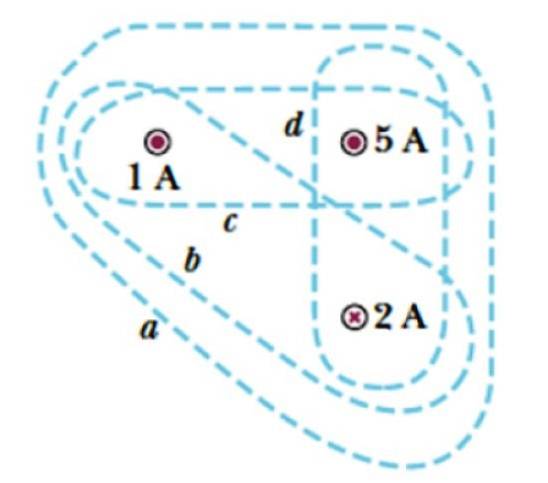
Løsning
Strømmene som kommer ut av papiret tildeles et + tegn. I følge dette:
Kurve a
Den omslutter de tre strømene, derfor er den medfølgende strømmen + 1 A + 5 A - 2 A = 4 A..
Kurve b
Bare strømmen til 1 A og - 2 A er innenfor denne kurven, derfor er den medfølgende strømmen - 2 A..
Kurve c
Den omslutter de utgående strømene 1A og 5 A, derfor er strømmen låst opp 6 A.
Kurve d
Strømmen inne i den er +5 A og - 2 A, så den inneholder en nettostrøm på 3 A..
- Øvelse 2
Beregn størrelsen på magnetfeltet som produseres av en veldig lang rett ledning, på et punkt som ligger 1 meter fra den, hvis ledningen har en strøm på 1 A.
Løsning
I følge Ampères lov er ledningens felt gitt av:
B = μellerI / 2πr = (4π x 10-7 x 1 / 2π x 1) T = 2 x 10-7 T.
Referanser
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volum 6. Elektromagnetisme. Redigert av Douglas Figueroa (USB).
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 2.
- Serway, R. 2009. College Physics. Cengage læring.
- Tipler, P. (2006) Fysikk for vitenskap og teknologi. 5. utg. Bind 2. Redaksjonell Reverté.


Ingen har kommentert denne artikkelen ennå.