
Klassemerke Hva det er for, hvordan få tak i det og eksempler
De klassemerke, Også kjent som midtpunktet, det er verdien som er i midten av en klasse, som representerer alle verdiene som er i den kategorien. Fundamentalt brukes klassemerke til å beregne visse parametere, for eksempel det aritmetiske gjennomsnittet eller standardavviket..
Klassemerket er altså midtpunktet for et hvilket som helst intervall. Denne verdien er også veldig nyttig for å finne variansen til et sett med data som allerede er gruppert i klasser, som igjen lar oss forstå hvor langt fra sentrum disse spesifikke dataene ligger.

Artikkelindeks
- 1 Frekvensfordeling
- 1.1 Hvor mange klasser du bør vurdere?
- 2 Hvordan får du det?
- 2.1 Eksempel
- 3 Hva er det til??
- 3.1 Eksempel
- 4 Referanser
Frekvensfordeling
For å forstå hva et klassemerke er, er begrepet frekvensfordeling nødvendig. Gitt et sett med data, er en frekvensfordeling en tabell som deler dataene i en rekke kategorier kalt klasser..
Nevnte tabell viser antall elementer som tilhører hver klasse; sistnevnte er kjent som frekvens.
I denne tabellen ofres en del av informasjonen vi får fra dataene, siden vi i stedet for å ha den individuelle verdien til hvert element, bare vet at den tilhører den klassen.
På den annen side får vi en bedre forståelse av datasettet, siden det på denne måten er lettere å sette pris på etablerte mønstre, som letter manipulering av nevnte data..
Hvor mange klasser du bør vurdere?
For å lage en frekvensfordeling, må vi først bestemme antall klasser vi vil ta og velge klassegrenser..
Å velge hvor mange klasser som skal ta skal være praktisk, med tanke på at et lite antall klasser kan skjule informasjon om dataene vi ønsker å studere, og en veldig stor kan generere for mange detaljer som ikke nødvendigvis er nyttige.
Faktorene vi må ta i betraktning når vi velger hvor mange klasser vi skal ta er flere, men blant disse to skiller seg ut: den første er å ta hensyn til hvor mye data vi må vurdere; det andre er å vite hvor stort distribusjonsområdet er (det vil si forskjellen mellom den største og minste observasjonen).
Etter å ha klassene allerede definert, fortsetter vi å telle hvor mye data som finnes i hver klasse. Dette tallet kalles frekvensen til klasser og er betegnet med fi.
Som vi tidligere hadde sagt, har vi at en frekvensfordeling mister informasjonen som kommer individuelt fra hver data eller observasjon. Av denne grunn blir det søkt etter en verdi som representerer hele klassen den tilhører; denne verdien er klassemerke.
Hvordan oppnås det?
Klassemerket er kjerneverdien som en klasse representerer. Det oppnås ved å legge til grensene for intervallet og dele denne verdien med to. Vi kunne uttrykke dette matematisk som følger:
xJeg= (Nedre grense + Øvre grense) / 2.
I dette uttrykket xJeg betegner merket til i-klasse.
Eksempel
Gitt følgende datasett, gi en representativ frekvensfordeling og få karakteren til tilsvarende klasser.

Siden dataene med den høyeste numeriske verdien er 391 og den laveste er 221, har vi at området er 391-221 = 170.
Vi velger 5 klasser, alle med samme størrelse. En måte å velge klasser på er som følger:

Merk at hver data er i en klasse, disse er usammenhengende og har samme verdi. En annen måte å velge klassene på er å vurdere dataene som en del av en kontinuerlig variabel, som kan nå enhver reell verdi. I dette tilfellet kan vi vurdere klasser av skjemaet:
205-245, 245-285, 285-325, 325-365, 365-405
Imidlertid kan denne måten å gruppere data på, presentere noen grenseoverskridelser. For eksempel, i tilfelle 245, oppstår spørsmålet: hvilken klasse tilhører den, den første eller den andre?
For å unngå denne forvirringen blir det laget en endepunktkonvensjon. På denne måten vil den første klassen være intervallet (205,245], den andre (245,285], og så videre.

Når klassene er definert, fortsetter vi med å beregne frekvensen, og vi har følgende tabell:
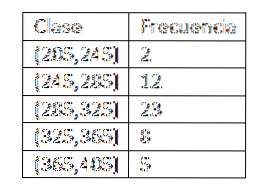
Etter å ha fått frekvensfordelingen av dataene, fortsetter vi med å finne klassemerker for hvert intervall. I virkeligheten må vi:
x1= (205+ 245) / 2 = 225
xto= (245+ 285) / 2 = 265
x3= (285+ 325) / 2 = 305
x4= (325+ 365) / 2 = 345
x5= (365+ 405) / 2 = 385
Vi kan representere dette med følgende graf:
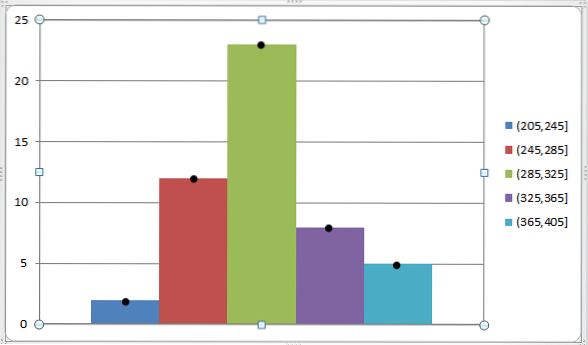
Hva er den til?
Som nevnt tidligere er klassemarkeringen veldig funksjonell for å finne det aritmetiske gjennomsnittet og variansen til en gruppe data som allerede er gruppert i forskjellige klasser..
Vi kan definere det aritmetiske gjennomsnittet som summen av observasjonene som er oppnådd mellom prøvestørrelsen. Fra et fysisk synspunkt er dens tolkning som likevektspunktet til et datasett.
Å identifisere et helt datasett med et enkelt nummer kan være risikabelt, så forskjellen mellom dette bruddpunktet og de faktiske dataene må også tas i betraktning. Disse verdiene er kjent som avvik fra det aritmetiske gjennomsnittet, og med disse søker vi å bestemme hvor mye det aritmetiske gjennomsnittet av dataene varierer..
Den vanligste måten å finne denne verdien på er variansen, som er gjennomsnittet av kvadratene til avvikene fra det aritmetiske gjennomsnittet.
For å beregne det aritmetiske gjennomsnittet og variansen til et datasett gruppert i en klasse bruker vi henholdsvis følgende formler:
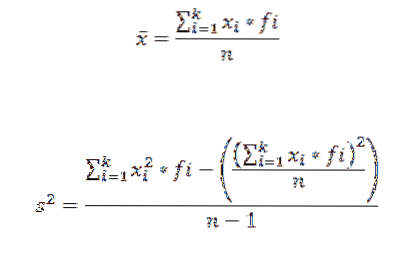
I disse uttrykkene xJeg er det i-klassemerket, fJeg representerer den korresponderende frekvensen og k antall klasser der dataene ble gruppert.
Eksempel
Ved å bruke dataene gitt i forrige eksempel, har vi at vi kan utvide dataene til frekvensfordelingstabellen litt mer. Du får følgende:
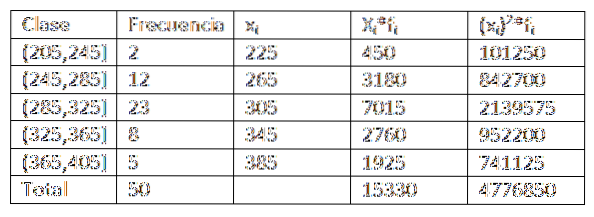
Deretter, ved å erstatte dataene i formelen, har vi igjen at det aritmetiske gjennomsnittet er:
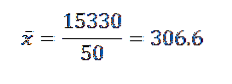
Dens avvik og standardavvik er:
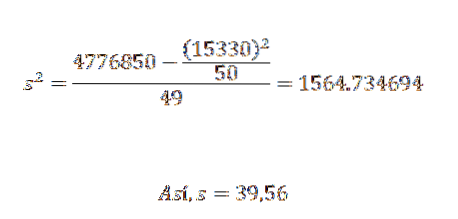
Fra dette kan vi konkludere med at de opprinnelige dataene har et aritmetisk gjennomsnitt på 306,6 og et standardavvik på 39,56..
Referanser
- Fernandez F. Santiago, Cordoba L. Alejandro, Cordero S. Jose M. Beskrivende statistikk. Esic Editorial.
- Johnson Richard A. Miller og Freund Probability and Statesmen for Engineers, Pearson Education.
- Miller I & Freund J. Probability and Statesmen for Engineers. TILBAKE.
- Sarabia A. Jose Maria, Pascual Marta. Grunnleggende statistikkurs for bedrifter
- Llinás S. Humberto, Rojas A. Carlos Beskrivende statistikk og sannsynlighetsfordeling, Universidad del Norte Editorial



Ingen har kommentert denne artikkelen ennå.