Tiltak for sentral tendens for grupperte dataformler, øvelser

De trendmål sentral de indikerer verdien dataene til en distribusjon ligger rundt. Det mest kjente er det gjennomsnittlige eller aritmetiske gjennomsnittet, som består i å legge til alle verdiene og dele resultatet med det totale antall data.

Imidlertid, hvis fordelingen består av et stort antall verdier og de ikke presenteres på en ryddig måte, er det ikke lett å utføre de nødvendige beregningene for å hente ut den verdifulle informasjonen de inneholder..

Det er derfor de er gruppert i klasser eller kategorier for å utvikle en distribusjon av frekvenser. Ved å utføre denne forrige bestillingen av dataene, er det da lettere å beregne tiltakene for sentral tendens, blant annet:

-Halv

-Median

-mote

-Geometrisk gjennomsnitt

-Harmonisk middel

Formler

Her er formlene for målingene av sentral tendens for de grupperte dataene:

Aritmetisk gjennomsnitt

Gjennomsnittet er det mest brukte for å karakterisere kvantitative data (numeriske verdier), selv om det er ganske følsomt for ekstreme verdier av fordelingen. Det beregnes av:

Med:

-X: gjennomsnitt eller aritmetisk gjennomsnitt

-F_Jeg: klassefrekvens

-m_Jeg: klassemerket

-g: antall klasser

-n: totale data

Median

For å beregne det er det nødvendig å finne intervallet som inneholder observasjonen n / 2 og interpolere for å bestemme den numeriske verdien for observasjonen, ved hjelp av følgende formel:

Hvor:

-c: bredden på intervallet som medianen tilhører

-B_M: nedre grense for intervallet

-F_m: antall observasjoner i intervallet

-n / 2: totale data delt på 2.

-F_BM: antall observasjoner før av intervallet som inneholder medianen.

Derfor er medianen et mål på posisjon, det vil si at den deler datasettet i to deler. De kan også defineres kvartiler, desiler Y persentiler, som deler fordelingen i henholdsvis fire, ti og hundre deler.

mote

I de samlede dataene blir det søkt i klassen eller kategorien som inneholder flest observasjoner. Dette er modal klasse. En distribusjon kan ha to eller flere moduser, i så fall kalles den bimodal Y multimodal, henholdsvis.

Du kan også beregne modusen i grupperte data etter ligningen:

Med:

-L₁: nedre grense for klassen der modusen er funnet

-Δ₁: trekk fra frekvensen til modalklassen og frekvensen til klassen som går foran den.

-Δ_to: trekk fra frekvensen til modalklassen og frekvensen til neste klasse.

-c: bredden på intervallet som inneholder modusen

Harmonisk middel

Det harmoniske gjennomsnittet er betegnet med H. Når du har et sett med n x-verdier₁, x_to, x₃..., Det harmoniske gjennomsnittet er det omvendte eller gjensidige av det aritmetiske gjennomsnittet av omvendt av verdiene.

Det er lettere å se det gjennom formelen:

Og når de grupperte dataene er tilgjengelige, blir uttrykket:

Hvor:

-H: harmonisk gjennomsnitt

-F_Jeg: klassefrekvens

-m_Jeg: klassemerke

-g: antall klasser

-N = f₁ + F_to + F₃ +...

Geometrisk gjennomsnitt

Hvis de har det n positive tall x₁, x_to, x₃…, Det geometriske gjennomsnittet G beregnes av den nte roten til produktet av alle tallene:

Når det gjelder grupperte data, kan det vises at desimallogaritmen til den geometriske gjennomsnittsloggen G er gitt av:

Hvor:

-G: geometrisk gjennomsnitt

-F_Jeg: klassefrekvens

-m_Jeg: klassemerket

-g: antall klasser

-N = f₁ + F_to + F₃ +...

Forholdet mellom H, G og X

Det er alltid sant at:

H ≤ G ≤ X

Mest brukte definisjoner

Følgende definisjoner kreves for å finne verdiene som er beskrevet i formlene ovenfor:

Frekvens

Frekvens er definert som antall ganger et stykke data gjentas.

Rang

Det er forskjellen mellom de høyeste og laveste verdiene, som er tilstede i fordelingen.

Antall klasser

For å vite i hvor mange klasser vi grupperer dataene, bruker vi noen kriterier, for eksempel følgende:

Grenser

De ekstreme verdiene for hver klasse eller intervall kalles grenser og hver klasse kan ha begge veldefinerte grenser, i så fall har den en lavere og en høyere grense. Eller det kan ha åpne grenser når et område er gitt, for eksempel verdier som er større eller mindre enn et bestemt tall.

Klassemerke

Det består ganske enkelt av midtpunktet i intervallet og beregnes ved å beregne gjennomsnittet av øvre og nedre grense.

Spaltebredde

Dataene kan grupperes i klasser av lik eller annen størrelse, dette er bredden eller bredden. Det første alternativet er det mest brukte, da det gjør beregningene mye enklere, selv om det i noen tilfeller er viktig at klassene har forskjellige bredder.

Bredden c Intervallet kan bestemmes av følgende formel:

c = Område / N_c

Hvor_c er antall klasser.

Treningen løst

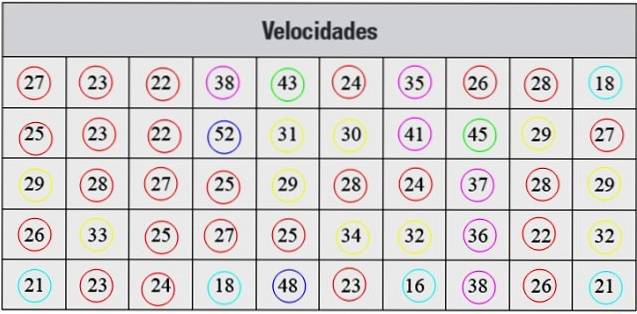
Nedenfor har vi en serie hastighetsmålinger i km / t, tatt med radar, som tilsvarer 50 biler som passerte gjennom en gate i en bestemt by:

Løsning

Dataene som presenteres på denne måten er ikke organisert, så det første trinnet er å gruppere dem i klasser.

Trinn for å gruppere dataene og lage tabellen

Trinn 1

Finn serien R:

R = (52 - 16) km / t = 36 km / t

Steg 2

Velg antall klasser N_c, i henhold til de gitte kriteriene. Siden det er 50 data, kan vi velge N_c = 6.

Trinn 3

Beregn bredde c av intervallet:

c = Område / N_c = 36/6 = 6

Trinn 4

Skjemaklasser og gruppedata som følger: for den første klassen blir en verdi litt mindre enn den laveste verdien som er tilstede i tabellen valgt som den nedre grensen, deretter legges verdien til c = 6, tidligere beregnet, til denne verdien, og dermed oppnår øvre grense for første klasse.

Vi fortsetter på samme måte med å bygge resten av klassene, som vist i følgende tabell:

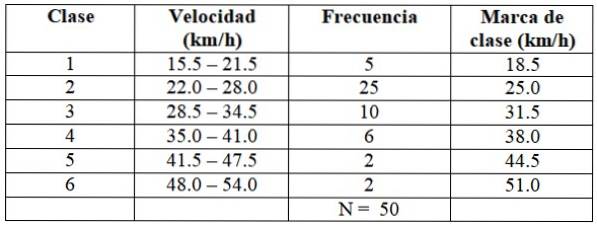
Hver frekvens tilsvarer en farge i figur 2, på denne måten sikres det at ingen verdi slipper å telles..

Beregning av gjennomsnittet

X = (5 x 18,5 + 25 x 25,0 + 10 x 31,5 + 6 x 38,0 + 2 x 44,5 + 2 x 51,0) ÷ 50 = 29,03 km / t

Beregning av medianen

Medianen er i klasse 2 i tabellen, siden det er de første 30 dataene for distribusjonen.

-Bredden på intervallet som medianen tilhører: c = 6

-Nedre grense for intervallet der medianen er: B_M = 22,0 km / t

-Antall observasjoner som intervallet f inneholder_m = 25

-Totale data delt på 2: 50/2 = 25

-Antall observasjoner det er før av intervallet som inneholder medianen: f_BM = 5

Og operasjonen er:

Median = 22,0 + [(25-5) ÷ 25] × 6 = 26,80 km / t

Mote beregning

Mote er også i klasse 2:

-Intervallbredde: c = 6

-Nedre grense for klassen der modusen finnes: L₁ = 22,0

-Trekk mellom frekvensen til modalklassen og frekvensen til klassen som går foran den: Δ₁ = 25-5 = 20

-Trekk mellom frekvensen til modalklassen og frekvensen til klassen som følger: Δ_to = 25 - 10 = 15

Med disse dataene er operasjonen:

Mode = 22,0 + [20 ÷ (20 + 15)] x6 = 25,4 km / t

Beregning av det geometriske gjennomsnittet

N = f₁ + F_to + F₃ +... = 50

logg = (5 x log 18,5 + 25 x log 25 + 10 x log 31,5 + 6 x log 38 + 2 × log 44,5 + 2 x log 51) / 50 =

logg G = 1,44916053

G = 28,13 km / t

Harmonisk middelberegning

1 / H = (1/50) x [(5 / 18,5) + (25/25) + (10 / 31,5) + (6/38) + (2 / 44,5) + (2/51)] = 0,0366

H = 27,32 km / t

Oppsummering av tiltak av sentral tendens

Enhetene til variablene er km / t:

-Gjennomsnitt: 29.03

-Median: 26.80

-Mote: 25.40

-Geometrisk gjennomsnitt: 28,13

-Harmonisk gjennomsnitt: 27,32

Referanser

1. Berenson, M. 1985. Statistikk for ledelse og økonomi. Interamericana S.A.
2. Canavos, G. 1988. Sannsynlighet og statistikk: Applikasjoner og metoder. Mcgraw hill.
3. Devore, J. 2012. Sannsynlighet og statistikk for ingeniørvitenskap og vitenskap. 8. plass. Utgave. Cengage.
4. Levin, R. 1988. Statistikk for administratorer. 2. plass. Utgave. Prentice hall.
5. Spiegel, M. 2009. Statistikk. Schaum-serien. 4. plass Utgave. Mcgraw hill.
6. Behandling av grupperte data. Gjenopprettet fra: itchihuahua.edu.mx.
7. Walpole, R. 2007. Sannsynlighet og statistikk for ingeniørfag og vitenskap. Pearson.