Dirac Jordan atommodellegenskaper og postulater

De Atommodell fra Dirac-Jordan er den relativistiske generaliseringen av den Hamilton-operatøren i ligningen som beskriver elektronens kvantebølgefunksjon. I motsetning til den forrige modellen, Schrodinger, er det ikke nødvendig å pålegge spinnet ved hjelp av Pauli-utelukkelsesprinsippet, siden det fremstår naturlig.

I tillegg inneholder Dirac-Jordan-modellen relativistiske korreksjoner, spin-bane-interaksjonen og Darwin-begrepet, som står for den fine strukturen til atomets elektroniske nivåer..

Fra 1928 satte forskerne Paul A. M. Dirac (1902-1984) og Pascual Jordan (1902-1980) seg til å generalisere kvantemekanikken utviklet av Schrodinger, for å inkludere Einsteins korreksjoner av spesiell relativitetsteori..

Dirac starter fra Schrodinger-ligningen, som består av en differensialoperatør, kalt en Hamiltonian, som opererer på en funksjon kjent som elektronbølgefunksjonen. Imidlertid tok Schrodinger ikke hensyn til de relativistiske effektene.

Løsningene til bølgefunksjonen tillater oss å beregne regionene der elektronet vil bli funnet rundt kjernen med en viss grad av sannsynlighet. Disse regionene eller sonene kalles orbitaler og avhenger av bestemte diskrete kvantetall, som definerer elektronens energi og vinkelmoment. 

Artikkelindeks

• 1 Postulater
  • 1.1 De fire postulatene til Dirac
• 2 Dirac-ligningen
  • 2.1 Dirac-Jordan-atomet
  • 2.2 Relativistiske korreksjoner til energispektret
• 3 Interessante artikler
• 4 Referanser

Postulater

I kvantemekaniske teorier, enten det er relativistisk eller ikke, er det ikke noe begrep om baner, siden verken elektronens posisjon eller hastighet kan spesifiseres samtidig. Og dessuten fører spesifisering av en av variablene til total upresisjon i den andre..

Hamiltonian er på sin side en matematisk operator som virker på kvantebølgefunksjonen og er bygget fra elektronens energi. For eksempel har et fritt elektron total energi E som avhenger av dets lineære momentum s og dermed:

E = (s^to) / 2m

For å konstruere Hamilton, starter vi fra dette uttrykket og erstatter s av kvanteoperatøren for momentum: 

s = -i ħ ∂ / ∂r 

Det er viktig å merke seg at vilkårene s Y s er forskjellige, siden den første er fremdriften, og den andre er den differensialoperatør assosiert med momentum. 

I tillegg er jeg den tenkte enheten og ħ Planck-konstanten delt på 2π, på denne måten oppnås den Hamilton-operatøren H av det frie elektronet:

H = (ħ^to/ 2m) ∂^to / ∂r^to 

For å finne Hamiltonens elektron i atomet, legg til interaksjonen mellom elektronet og kjernen: 

H = (ħ2 / 2m) ∂^to / ∂r^to  - eΦ (r)

I det forrige uttrykket -e er elektronens elektriske ladning og Φ (r) er det elektrostatiske potensialet som produseres av den sentrale kjernen.

Nå virker operatøren H på bølgefunksjonen ψ i henhold til Schrodinger-ligningen, som er skrevet slik:

H ψ = (i ħ ∂ / ∂t) ψ

Diracs fire postulater

Første postulat: Den relativistiske bølge ligningen har samme struktur som Schrodinger bølge ligningen. Det som endres er H:

H ψ = (i ħ ∂ / ∂t) ψ

Andre postulat: Hamilton-operatøren er konstruert med utgangspunkt i Einsteins energimomentforhold, som er skrevet som følger:

E = (m^to c⁴ + s^to c^to)^1/2

I det forrige forholdet, hvis partikkelen har momentum p = 0, har vi den berømte ligningen E = mc^to som relaterer hvilenergien til en hvilken som helst massepartikkel m til lysets hastighet c.

Tredje postulat: for å oppnå den Hamilton-operatøren brukes den samme kvantiseringsregelen som brukes i Schrodinger-ligningen:

s = -i ħ ∂ / ∂r

I begynnelsen var det ikke klart hvordan man skulle håndtere denne differensialoperatøren som handlet innenfor en kvadratrot, så Dirac satte seg for å skaffe seg en lineær Hamilton-operatør på momentumoperatøren, og derfra oppsto hans fjerde postulat.

Fjerde postulat: for å kvitte seg med kvadratroten i den relativistiske energiformelen, foreslo Dirac følgende struktur for E^to:

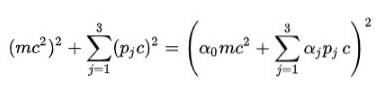
Selvfølgelig er det nødvendig å bestemme alfakoeffisientene (α0, α1, α2, α3) for at dette skal være sant.

Diracs ligning

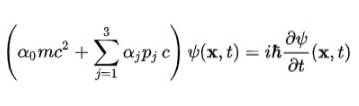
I sin kompakte form regnes Dirac-ligningen som en av de vakreste matematiske ligningene i verden:

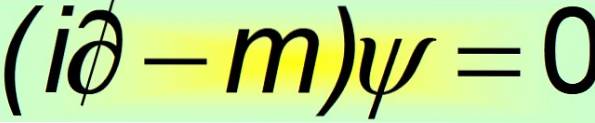
Og det er da det blir klart at den konstante alfas ikke kan være skalære størrelser. Den eneste måten som likheten til det fjerde postulatet oppfylles, er at de er 4 × 4 konstante matriser, som er kjent som Dirac matriser:

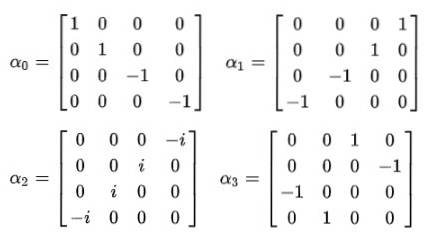
Det observeres umiddelbart at bølgefunksjonen slutter å være en skalarfunksjon og blir en firekomponentvektor kalt spinor:

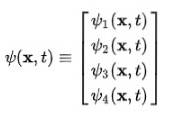
Dirac-Jordan-atomet

For å oppnå atommodellen er det nødvendig å gå fra ligningen til det frie elektronet til det til elektronet i det elektromagnetiske feltet produsert av atomkjernen. Denne interaksjonen tas i betraktning ved å innlemme skalarpotensialet Φ og vektorpotensialet TIL i Hamiltonian:

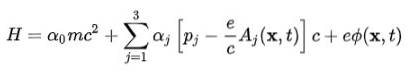
Bølgefunksjonen (spinor) som skyldes inkorporering av denne Hamilton har følgende egenskaper: 

- Den oppfyller spesiell relativitet, siden den tar hensyn til elektronens indre energi (første periode av det relativistiske Hamiltonian)

- Den har fire løsninger som tilsvarer de fire komponentene i spinor

- De to første løsningene tilsvarer den ene til + + ½ og den andre for å spinne - ½ 

- Til slutt forutsier de to andre løsningene eksistensen av antimateriale, siden de tilsvarer positroner med motsatte spinn..

Den store fordelen med Dirac-ligningen er at korreksjonene til den grunnleggende Schrodinger Hamiltonian H (o) kan brytes ned i flere termer som vi vil vise nedenfor:

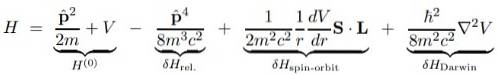
I det forrige uttrykket er V det skalære potensialet, siden vektorpotensialet TIL er null hvis den sentrale protonen antas å være stasjonær og derfor ikke vises.

Årsaken til at Dirac-korreksjonene til Schrodinger-løsningene i bølgefunksjonen er subtile. De oppstår fra det faktum at de tre siste begrepene i den korrigerte Hamiltonianen er delt med hastigheten c av lys i kvadrat, et enormt tall, noe som gjør disse begrepene numerisk små.

Relativistiske korreksjoner til energispektret

Ved å bruke Dirac-Jordan-ligningen finner vi korreksjoner til energispektret til elektronet i hydrogenatomet. Korrigeringer for energi i atomer med mer enn ett elektron i omtrentlig form er også funnet gjennom en metodikk kjent som forstyrrelsesteori..

Tilsvarende tillater Dirac-modellen å finne den korreksjonen av fin struktur i hydrogenenerginivåer.. 

Imidlertid oppnås enda mer subtile korreksjoner som hyperfin struktur og lamskift fra mer avanserte modeller som kvantefeltsteori, som ble født nettopp av bidragene fra Dirac-modellen.

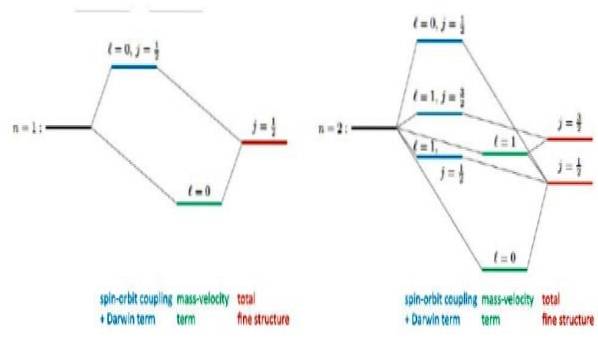
Følgende figur viser hvordan Diracs relativistiske korreksjoner til energinivå ser ut:

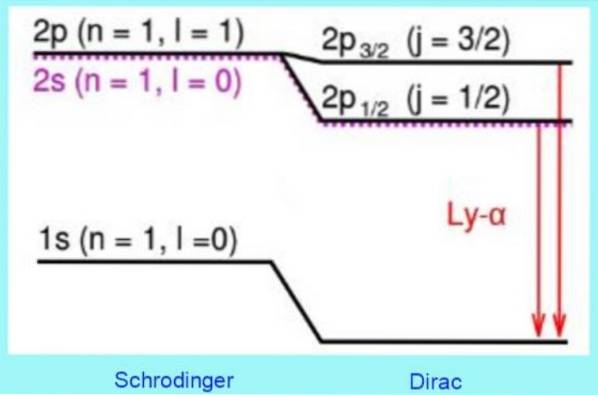
For eksempel forutsier løsninger på Dirac-ligningen riktig et observert skifte på nivå 2s. Det er den velkjente korreksjonen av fin struktur i Lyman-alfa linjen i hydrogenspektret (se figur 3).

Forresten, den fine strukturen er navnet i atomfysikk for dobling av linjene til utslippsspekteret til atomer, som er en direkte konsekvens av elektronisk spinn..

Artikler av interesse

Atomic de Broglie-modellen.

Chadwick Atomic Model.

Heisenberg atommodell.

Perrins atommodell.

Thomsons atommodell.

Dalton atommodell.

Schrödingers atommodell.

Atomic model of Democritus.

Atomisk modell av Leucippus.

Bohr atommodell.

Nåværende atommodell.

Referanser

1. Atomteori. Gjenopprettet fra wikipedia.org.
2. Elektronmagnetisk øyeblikk. Gjenopprettet fra wikipedia.org.
3. Quanta: En konseptbok. (1974). Oxford University Press. Gjenopprettet fra Wikipedia.org.
4. Dirac Jordan atommodell. Gjenopprettet fra prezi.com.
5. Det nye kvanteuniverset. Cambridge University Press. Gjenopprettet fra Wikipedia.org.