
Kvantemekanisk modell av atomatferden, eksempler
De kvantemekanisk modell av atomet antar at dette er dannet av en sentral kjerne som består av protoner og nøytroner. Negativt ladede elektroner omgir kjernen i diffuse områder kjent som orbitaler..
Formen og omfanget av elektroniske orbitaler bestemmes av forskjellige størrelser: kjernens potensial og de kvantiserte energinivåene og elektronvinkelmomentet.
I henhold til kvantemekanikk har elektroner to bølgepartikkelatferd, og i atomskala er de diffuse og ikke-punktale. Atomens dimensjoner bestemmes praktisk talt av utvidelsen av de elektroniske orbitalene som omgir den positive kjernen.
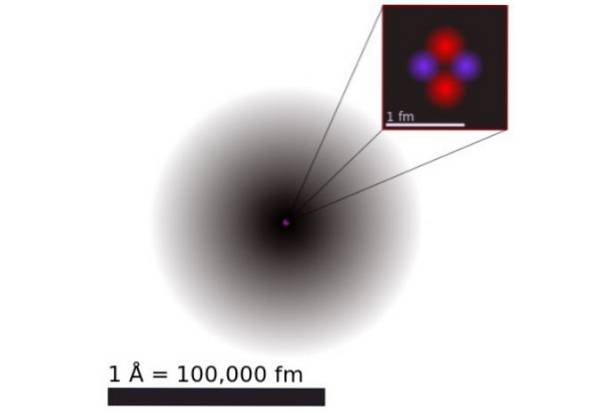
Figur 1 viser strukturen til heliumatomet, som har en kjerne med to protoner og to nøytroner. Denne kjernen er omgitt av skyen av sannsynlighet for de to elektronene som omgir kjernen, som er hundre tusen ganger mindre. I det følgende bildet kan du se heliumatomet, med protonene og nøytronene i kjernen og elektronene i orbitaler.

Størrelsen på et heliumatom er i størrelsesorden ett angstrøm (1 Å), det vil si 1 x 10 ^ -10 m. Mens størrelsen på kjernen er i størrelsesorden a femtometer (1 fm), det vil si 1 x 10 ^ -15 m.
Til tross for at den er så relativt liten, er 99,9% av atomvekten konsentrert i den lille kjernen. Dette er fordi protonene og nøytronene er 2000 ganger tyngre enn elektronene som omgir dem..
Artikkelindeks
- 1 Atomskala og kvanteoppførsel
- 1.1 Første kvantemodeller
- 2 Dynamikk av materialbølger
- 2.1 Atomiske orbitaler
- 2.2 Kvantetall
- 3 Form og størrelse på orbitaler
- 3.1 Spinnet
- 4 Referanser
Atomskala og kvanteoppførsel
Et av konseptene som hadde mest innflytelse på utviklingen av atommodellen var dualiteten bølge - partikkel: oppdagelsen at hvert materielt objekt har en materiebølge knyttet til seg.
Formelen for beregning av bølgelengden λ knyttet til et materielt objekt ble foreslått av Louis De Broglie i 1924 og er følgende:
λ = h / (m v)
Hvor h er Plancks konstant, m deigen og v hastighet.
I henhold til De Broglies prinsipp har hvert objekt en dobbel oppførsel, men avhengig av omfanget av interaksjonene, hastigheten og massen, kan bølgeoppførselen være mer fremtredende enn partikkelatferden eller omvendt..
Elektronen er lett, dens masse er 9,1 × 10 ^ -31 kg. Den typiske hastigheten til et elektron er 6000 km / s (femti ganger tregere enn lysets hastighet). Denne hastigheten tilsvarer energiverdier i området ti titalls volt..
Med ovennevnte data, og ved å bruke de Broglie-formelen, kan bølgelengden for elektronet oppnås:
λ = 6,6 x 10 ^ -34 J s / (9,1 × 10 ^ -31 kg 6 x 10 ^ 6 m / s) = 1 x 10 ^ -10 m = 1 Å
Elektronet ved de typiske energiene til atomnivåer har en bølgelengde av samme størrelsesorden som atomskalaen, slik at den på den skalaen har en bølgeatferd og ikke en partikkel..
Første kvantemodeller
Med tanken om at atomskalaelektronen har bølgeatferd, ble de første atommodellene basert på kvanteprinsipper utviklet. Blant disse skiller Bohr-atommodellen seg ut, som perfekt forutsa utslippsspekteret av hydrogen, men ikke det for andre atomer.
Bohr-modellen, og senere Sommerfeld-modellen, var semi-klassiske modeller. Det vil si at elektronet ble behandlet som en partikkel utsatt for den elektrostatiske tiltrekningskraften til kjernen som kretset rundt den, styrt av Newtons andre lov..
I tillegg til klassiske baner tok disse første modellene hensyn til at elektronet hadde en tilhørende materialbølge. Bare baner hvis omkrets var et helt antall bølgelengder var tillatt, siden de som ikke oppfyller dette kriteriet forsvinner av destruktiv interferens..
Det er da kvantiseringen av energi vises for første gang i atomstrukturen..
Ordet kvante Det kommer nettopp fra det faktum at elektronet bare kan ta på seg noen diskrete energiverdier i atomet. Dette sammenfaller med Plancks funn, som besto i oppdagelsen at en stråling av frekvens F samhandler med materie i pakker med energi E = h f, hvor h er Plancks konstant.
Dynamikk av materialbølger
Det var ikke lenger tvil om at elektronet på atomnivå oppførte seg som en materialbølge. Det neste trinnet var å finne ligningen som styrer deres oppførsel. Denne ligningen er verken mer eller mindre enn Schrodinger-ligningen, foreslått i 1925.
Denne ligningen forholder seg til og bestemmer bølgefunksjonen ψ assosiert med en partikkel, slik som elektronet, med dets interaksjonspotensial og dets totale energi OG. Dens matematiske uttrykk er:


Likhet i Schrodinger-ligningen holder bare for noen verdier av den totale energien OG, som gir opphav til kvantisering av energi. Bølgefunksjonen til elektronene som utsettes for kjernens potensial er oppnådd fra løsningen av Schrodinger-ligningen.
Atomiske orbitaler
Den absolutte verdien av bølgefunksjonen i kvadrat |ψ| ^ 2, gir sannsynlighetsamplituden for å finne elektronet i en gitt posisjon.
Dette fører til begrepet orbital, som er definert som det diffuse området okkupert av elektronet med ikke-null sannsynlighetsamplitude, for de diskrete verdiene av energi og vinkelmoment bestemt av løsningene i Schrodinger-ligningen.
Kunnskapen om orbitalene er veldig viktig, fordi den beskriver atomstrukturen, den kjemiske reaktiviteten og de mulige bindingene til å danne molekyler.
Hydrogenatomet er det enkleste av alt, fordi det har et enslig elektron og det er det eneste som innrømmer en nøyaktig analytisk løsning av Schrodinger-ligningen.
Dette enkle atomet har en kjerne som består av et proton, som produserer et sentralt potensial for Coulomb-tiltrekning som bare avhenger av radiusen. r, så det er et system med sfærisk symmetri.
Bølgefunksjonen avhenger av posisjonen gitt av de sfæriske koordinatene i forhold til kjernen, siden det elektriske potensialet har sentral symmetri.
Videre kan bølgefunksjonen skrives som et produkt av en funksjon som bare avhenger av den radiale koordinaten, og en annen som avhenger av vinkelkoordinatene:

Kvantetall
Løsningen av den radiale ligningen produserer de diskrete energiverdiene, som avhenger av et helt tall n, ringte hovedkvantetall, som kan ta positive heltallverdier 1, 2, 3, ...
Diskrete energiverdier er negative verdier gitt av følgende formel:

Vinkelligningsløsningen definerer de kvantiserte verdiene til vinkelmomentet og dets z-komponent, noe som gir opphav til kvantetallene l Y ml.
Kvantetallet for vinkelmomentet l går fra 0 til n-1. Kvantumnummer ml kalles det magnetiske kvantetallet og går fra -l før +l. For eksempel ja l var 2 det magnetiske kvantetallet ville ta verdiene -2, -1, 0, 1, 2.
Orbitalens form og størrelse
Orbitalens radiale rekkevidde bestemmes av radi bølgefunksjontil. Det er større når energien til elektronet øker, det vil si når det viktigste kvantetallet øker.
Den radiale avstanden måles vanligvis i Bohr-radier, som for den laveste energien av hydrogen er 5,3 X 10-11 m = 0,53 Å.

Men formen på orbitalene bestemmes av verdien av kvantumkvantumtallet. Hvis l = 0 har vi en sfærisk bane kalt s, hvis l = 1 har vi en lobulert bane kalt s, som kan ha tre retninger i henhold til det magnetiske kvantetallet. Følgende figur viser formen på orbitalene.
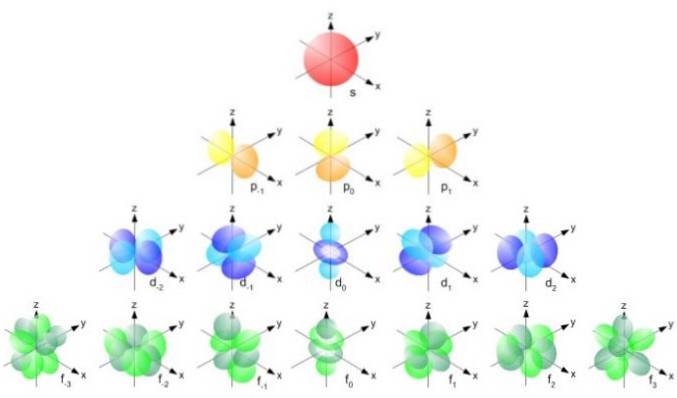
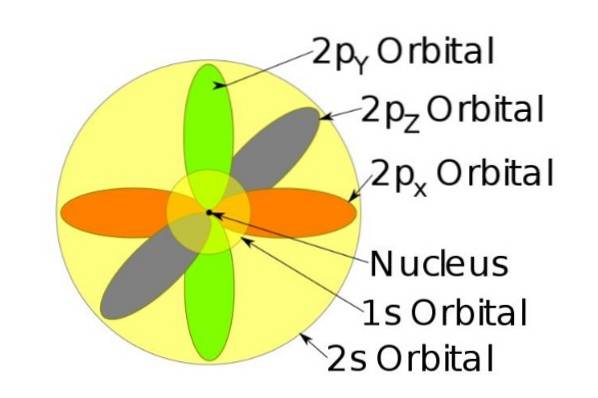
Disse orbitalene pakkes inn i hverandre i henhold til energien til elektronene. For eksempel viser følgende figur orbitalene i et natriumatom.
Snurret
Den kvantemekaniske modellen til Schrödinger-ligningen inneholder ikke elektronets spinn. Men det tas i betraktning gjennom Pauli-ekskluderingsprinsippet, som indikerer at orbitaler kan befolkes med opptil to elektroner med spinnkvantantall s = + ½ og s = -½.
For eksempel har natriumionen 10 elektroner, det vil si at hvis vi refererer til forrige figur, er det to elektroner for hver bane.
Men hvis det er det nøytrale natriumatomet, er det 11 elektroner, hvorav den siste vil okkupere en 3s orbital (ikke vist på figuren og med en større radius enn 2s). Spinnet i atomet er avgjørende for de magnetiske egenskapene til et stoff.
Referanser
- Alonso - Finn. Kvante- og statistiske grunnlag. Addison Wesley.
- Eisberg - Resnick. Kvantefysikk. Limusa - Wiley.
- Gasiorowicz. Kvantefysikk. John Wiley & Sons.
- HSC. Fysikkurs 2. Jacaranda pluss.
- Wikipedia. Schrodingers atommodell. Gjenopprettet fra: Wikipedia.com



Ingen har kommentert denne artikkelen ennå.