Dreiemomentegenskaper og formler, øvelser

De dreiemoment, moment eller moment av en kraft er evnen til en kraft til å forårsake en sving. Etymologisk får den navnet torque som en avledning av det engelske ordet dreiemoment, fra latin torquere (vri).

Dreiemomentet (i forhold til et gitt punkt) er den fysiske størrelsen som oppstår ved å lage vektorproduktet mellom posisjonsvektorene til punktet der kraften påføres og den av den utøvde kraften (i den angitte rekkefølgen). Dette øyeblikket avhenger av tre hovedelementer.

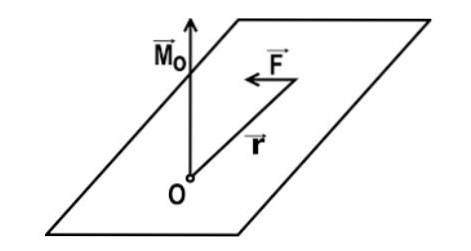
Det første av disse elementene er størrelsen på den påførte kraften, den andre er avstanden mellom punktet der den påføres og punktet med hensyn til hvilket kroppen roterer (også kalt spakarmen), og det tredje elementet er vinkelen av anvendelse av nevnte styrke.

Jo større kraft, jo større spinn. Det samme skjer med spakarmen: jo større avstand mellom punktet hvor kraften påføres og det punktet som den gir sving til, jo større vil dette være.

Selvfølgelig er dreiemomentet av spesiell interesse for bygg og industri, så vel som det er til stede i utallige bruksområder for hjemmet, for eksempel når en mutter strammes med en skiftenøkkel..

Artikkelindeks

• 1 Formler
  • 1.1 Enheter
• 2 funksjoner
• 3 Resulterende dreiemoment
• 4 Søknader
• 5 Øvelser løst
  • 5.1 Øvelse 1
  • 5.2 Øvelse 2
• 6 Referanser

Formler

Det matematiske uttrykket for dreiemomentet til en kraft i forhold til et punkt O er gitt av: M = r x F

I dette uttrykket er r vektoren som forbinder punktet O med punktet P for påføring av kraften, og F er vektoren for den påførte kraften.

Momentets måleenheter er N ∙ m, som, selv om de er dimensjonalt ekvivalente med Joule (J), har en annen betydning og ikke bør forveksles.

Derfor tar dreiemomentmodulen verdien gitt av følgende uttrykk:

M = r ∙ F ∙ sin α

I dette uttrykket er α vinkelen mellom kraftvektoren og vektoren r eller spakarmen. Dreiemomentet betraktes som positivt hvis kroppen roterer mot klokken; tvert imot, det er negativt når det roterer med klokken.

Enheter

Som allerede nevnt ovenfor, er måleenheten til dreiemomentet resultatet av produktet av en kraftenhet og en avstandsenhet. Nærmere bestemt bruker det internasjonale systemet for enheter Newton-måleren hvis symbol er N • m.

På et dimensjonsnivå kan newtonmåleren virke ekvivalent med joule; Imidlertid bør juli ikke brukes til å uttrykke øyeblikk. Joule er en enhet for å måle verk eller energier som fra et konseptuelt synspunkt er veldig forskjellige fra vridningsmomenter.

På samme måte har torsjonsmomentet et vektorkarakter, som er både skalararbeidet og energien.

Kjennetegn

Av det som er sett følger det at momentet til en kraft i forhold til et punkt representerer kapasiteten til en kraft eller et sett av krefter for å modifisere rotasjonen av legemet rundt en akse som passerer gjennom punktet..

Derfor genererer torsjonsmomentet en vinkelakselerasjon på kroppen og er størrelsen på et vektorkarakter (slik at det er definert fra en modul, en retning og en følelse) som er tilstede i mekanismene som har blitt utsatt for vridning eller bøyning.

Dreiemomentet vil være null hvis kraftvektoren og vektoren r har samme retning, siden i så fall verdien av sin α vil være null.

Resulterende dreiemoment

Gitt et bestemt legeme som en serie krefter virker på, hvis de påførte kreftene virker i samme plan, dreiemomentet som følge av påføringen av alle disse kreftene; er summen av torsjonsmomentene som skyldes hver kraft. Derfor er det sant at:

M_T = ∑ M = M₁ + M_{to +} M₃ +...

Selvfølgelig er det nødvendig å ta hensyn til tegnkriteriet for torsjonsmomenter, som forklart ovenfor.

applikasjoner

Dreiemomentet er tilstede i applikasjoner så hver dag som å stramme en mutter med en skiftenøkkel, eller åpne eller lukke en kran eller en dør.

Imidlertid går applikasjonene mye lenger; dreiemomentet finnes også i maskinens akser eller i resultatet av innsatsen som bjelkene utsettes for. Derfor er applikasjonene innen industri og mekanikk mange og varierte..

Løst øvelser

Nedenfor er et par øvelser for å gjøre det lettere å forstå ovennevnte.

Øvelse 1

Gitt følgende figur der avstandene mellom punkt O og punkt A og B er henholdsvis 10 cm og 20 cm:

a) Beregn verdien av dreiemomentets modul i forhold til punkt O hvis en kraft på 20 N påføres punkt A.

b) Beregn hva som må være verdien av kraften som påføres i B for å oppnå samme dreiemoment som oppnådd i forrige avsnitt.

Løsning

For det første er det praktisk å overføre dataene til enheter i det internasjonale systemet.

r_TIL = 0,1 m

r_B = 0,2 m

a) For å beregne dreiemomentmodulen bruker vi følgende formel:

M = r ∙ F ∙ sin α = 0,1 ∙ 20 ∙ 1 = 2 N ∙ m

b) For å bestemme den etterspurte styrken, fortsett på en lignende måte:

M = r ∙ F ∙ sin α = 0,2 ∙ F ∙ 1 = 2 N ∙ m

Løsning for F oppnås at:

F = 10 N

Øvelse 2

En kvinne utøver en styrke på 20 N på enden av en 30 cm lang skiftenøkkel. Hvis kraftvinkelen med skiftenøkkelhåndtaket er 30 °, hva er dreiemomentet på mutteren??

Løsning

Følgende formel brukes og operasjonen utføres:

M = r ∙ F ∙ sin α = 0,3 ∙ 20 ∙ 0,5 = 3 N ∙ m

Referanser

1. Kraftmoment. (n.d.). På Wikipedia. Hentet 14. mai 2018 fra es.wikipedia.org.
2. Moment (n.d.). I Wikipedia. Hentet 14. mai 2018 fra en.wikipedia.org.
3. Serway, R. A. og Jewett, Jr. J.W. (2003). Fysikk for forskere og ingeniører. 6. utgave Brooks Cole.
4. Marion, Jerry B. (1996). Klassisk dynamikk av partikler og systemer. Barcelona: Ed. Reverté.
5. Kleppner, Daniel; Kolenkow, Robert (1973). En introduksjon til mekanikk. McGraw-Hill.