I elliptisk bevegelse beskriver mobilen en ellips, akkurat som planetene gjør rundt solen, og månen og kunstige satellitter rundt jorden, for å nevne noen kjente eksempler..
Kraften som gir opphav til denne bevegelsen er tyngdekraften, en sentral kraft. Denne typen krefter er rettet mot (eller fra) et fast punkt O, og deres modul avhenger av avstanden til det punktet. Hvis r er avstanden og ellerr er enhetsvektoren i radiell retning, den sentrale kraften F er en vektorfunksjon av formen:
F = F (r) ellerr
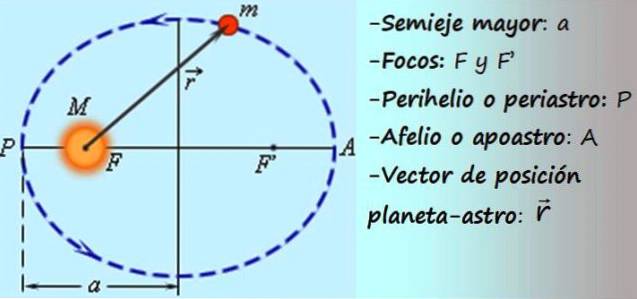
Med noen matematikker kan det vises at bevegelsen til et objekt under tyngdekraftens virkning følger en av disse fire banene: ellips, omkrets, hyperbola eller parabel.
Noen av hovedegenskapene til elliptisk bevegelse under sentral styrke er:
-Vinkelmomentet med hensyn til O er bevart, kalt L og som beregnes gjennom vektorproduktet mellom posisjons- og hastighetsvektorene: L = r × mv, hvor m representerer massen til det bevegelige objektet.
-Den elliptiske banen ligger i planet bestemt av vektorene r Y v.
-Fra bevaring av vinkelmoment den såkalte lov om områder, som fastslår at mobilen reiser like områder på like tider.
-Mekanisk energi konserveres også i elliptisk bevegelse, hvis det ikke er noen dissipative krefter.
-Tiden det tar for mobilen å gi en bane og dens totale energi, avhenger bare av lengden "a" til ellipsens semi-hovedakse..
Selv om objektet beveger seg i en lukket og repeterende bane i sirkulær og elliptisk bevegelse, det vil si periodisk, er det åpenbare forskjeller mellom en bevegelse og en annen, for eksempel:
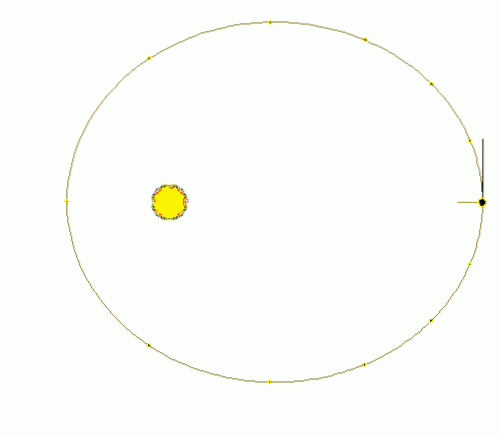
-I sirkulær bevegelse beskriver mobilen en omkrets, hvis radius (avstand til sentrum av stien) er konstant, mens den i elliptisk bevegelse beskriver en ellipse, der avstanden til sentrum av stien er variabel (se figur 1).
-I tilfelle av ensartet sirkulær bevegelse MCU, sveiper mobilen like vinkler på like tid, men i planet elliptisk bevegelse blir like områder feid på like tid. Dette er loven i områder, også kjent som Keplers andre lov om planetbevegelse..
I elliptisk bevegelse avledet fra gravitasjonsattraksjon er perioden T bevegelse den tiden det tar for planeten eller satellitten (m) å gjøre en elliptisk sving rundt solen eller jorden (M). Ved å bruke bevaring av energi følger det at den er proporsjonal med kuben til lengden på ellipsens semi-hovedakse:
Der G er den universelle gravitasjonskonstanten: 6,67 × 10-elleve N ∙ mto/ kgto, M er solens, jordens eller gjenstandens masse som forårsaker samspillet på m og "a" er lengden på den semi-hovedaksen.
Den totale energien for planeten (m) - Sun (M) -systemet er:
Størrelsen på vinkelmomentet ved et punkt på den elliptiske bane avhenger også av lengden på den semi-hovedaksen, samt på eksentrisiteten "e", en dimensjonsfri parameter som indikerer hvor flatt ellipsen er. Hvis e = 0, blir ellipsen en sirkel.
Størrelsen på hastigheten er gitt av følgende ligning:
Hvor r er avstanden mellom et punkt på bane (plassering av planeten) og fokus (sol).
Keplers første lov sier at bevegelsen av planetene rundt solen følger en elliptisk vei, med solen i en av fokussene. Noen kometer som med jevne mellomrom besøker jorden, som Halleys komet, følger også en elliptisk bevegelse..
Bortsett fra denne elliptiske translasjonsbevegelsen og rotasjonen rundt aksen, har planetene sine egne bevegelser på grunn av de komplekse gravitasjonsinteraksjonene med de andre planetene og himmellegemene i solsystemet. På denne måten er det presesjons- og nutasjonsbevegelsene som jorden har, og som skyldes den felles gravitasjonsattraksjonen til solen og månen..
I presesjon beskriver jordaksen en kjegle når den roterer rundt aksen vinkelrett på planen eller ekliptikken. Og i nutasjon, som er lagt over på presesjon, svinger jordaksen opp og ned i en elliptisk sløyfe hvert 18,6 år. Totalt 1385 av disse løkkene siden på 25 767 år, som er perioden med nedgangen til jordaksen.
I havvann utfører en partikkel en elliptisk bevegelse, med ellipsen som blir mer og mer flat med økende dybde. På den annen side, når vannet er dypt, er partikkelenes bevegelse sirkulær.
Det som skjer er at når bølgen nærmer seg kysten, vises friksjonskrefter takket være dens nærhet til bunnen, og denne friksjonen har en tendens til å bremse bevegelsen i den nedre delen av banen, mens toppen fortsetter bevegelsen..
Resultatet er at omkretsen flater, og effekten forsterkes når dybden øker..
En fysisk pendel består av et stivt fast stoff som kan svinge i et plan rundt en akse vinkelrett på den. Hvis gjenstanden får bevege seg fritt, kan den beskrive hvilken som helst vinkel rundt aksen som forbinder massesenteret med opphengspunktet, samt rotere rundt den..
Takket være jordens rotasjon, er pendelen i stand til å beskrive baner med omtrent elliptisk form, som er kjent som elliptisk svingemodus, preget av en annen vinkelmoment enn 0.
Det er også planmodus (vinkelmoment 0) og konisk modus (vinkelmoment annet enn 0), sistnevnte med en sirkulær bane på et horisontalt plan.
De elliptiske bevegelsene som er beskrevet tidligere, forekommer i naturen, men kan også brukes til å lage nyttige dingser, som elliptiske sykler, som er veldig populære maskiner for aerobic..
De er stasjonære sykler som i utgangspunktet består av et styr og to pedaler som personen aktiverer ved å skyve seg selv med vekten, og beskrive en ellips med føttene. Dette er en naturlig bevegelse med lite innvirkning som er gunstig fordi den beveger mange muskelgrupper i hele kroppen..
Ingen har kommentert denne artikkelen ennå.