De tilfeldig prøvetaking det er måten å velge et statistisk representativt utvalg fra en gitt populasjon. En del av prinsippet om at hvert element i prøven skal ha samme sannsynlighet for å bli valgt.
En uavgjort er et eksempel på tilfeldig utvalg, der hvert medlem av deltakerpopulasjonen tildeles et nummer. For å velge tallene som tilsvarer loddpremiene (prøven), brukes en tilfeldig teknikk, for eksempel å hente ut tallene som ble registrert på identiske kort fra en postkasse.
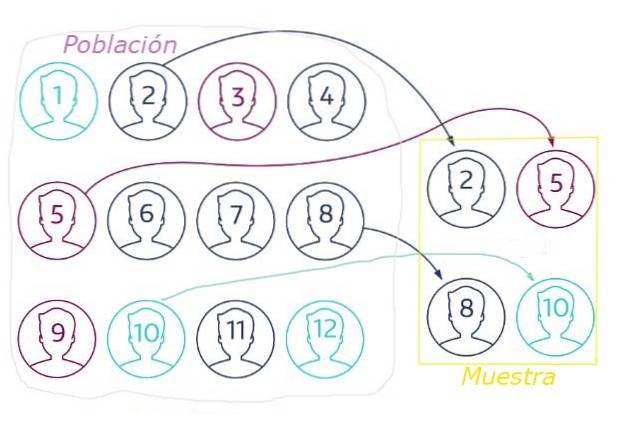
Ved tilfeldig prøvetaking er det viktig å velge utvalgsstørrelse riktig, fordi et ikke-representativt utvalg av befolkningen kan føre til feil konklusjoner på grunn av statistiske svingninger..
Artikkelindeks
Det finnes formler for å bestemme riktig størrelse på et utvalg. Den viktigste faktoren å vurdere er om populasjonsstørrelsen er kjent eller ikke. La oss se på formlene for å bestemme prøvestørrelsen:
Når populasjonsstørrelsen N er ukjent, er det mulig å velge et utvalg av tilstrekkelig størrelse n, for å avgjøre om en bestemt hypotese er sann eller falsk.
For dette brukes følgende formel:
n = (Zto p q) / (E.to)
Hvor:
-p er sannsynligheten for at hypotesen er sann.
-q er sannsynligheten for at den ikke er det, derfor er q = 1 - p.
-E er den relative feilmarginen, for eksempel har en feil på 5% en margin E = 0,05.
-Z har å gjøre med nivået på selvtillit som kreves av studien.
I en standardisert (eller normalisert) normalfordeling har et konfidensnivå på 90% Z = 1,645, fordi sannsynligheten for at resultatet er mellom -1,645σ og + 1,645σ er 90%, der σ er standardavviket.
1.- 50% konfidensnivå tilsvarer Z = 0,675.
2.- 68,3% konfidensnivå tilsvarer Z = 1.
3.- 90% konfidensnivå tilsvarer Z = 1.645.
4.- 95% konfidensnivå tilsvarer Z = 1,96
5.- 95,5% konfidensnivå tilsvarer Z = 2.
6.- 99,7% konfidensnivå tilsvarer Z = 3.
Et eksempel der denne formelen kan brukes, vil være i en studie for å bestemme gjennomsnittsvekten av småstein på en strand.
Det er tydelig at det ikke er mulig å studere og veie alle småsteinene på stranden, så det anbefales å trekke ut en prøve så tilfeldig som mulig og med riktig antall elementer..
Når antall N av elementene som utgjør en bestemt populasjon (eller univers) er kjent, hvis du vil velge et statistisk signifikant utvalg av størrelse n ved enkel tilfeldig prøvetaking, er dette formelen:
n = (Ztop q N) / (N Eto + Ztop q)
Hvor:
-Z er koeffisienten assosiert med konfidensnivået.
-p er sannsynligheten for at hypotesen lykkes.
-q er sannsynligheten for feil i hypotesen, p + q = 1.
-N er størrelsen på den totale befolkningen.
-E er den relative feilen i studieresultatet.
Metoden for å trekke ut prøvene avhenger mye av hvilken type undersøkelse som må gjøres. Derfor har tilfeldig prøvetaking et uendelig antall applikasjoner:
I telefonundersøkelser velges for eksempel personene som skal konsulteres ved hjelp av en tilfeldig tallgenerator, som gjelder for regionen som studeres..
Hvis du vil bruke et spørreskjema til de ansatte i et stort selskap, kan du ty til utvalget av respondentene gjennom deres ansattnummer eller identitetskortnummer..
Dette tallet må også velges tilfeldig, for eksempel ved å bruke en tilfeldig tallgenerator.
I tilfelle studien er på deler produsert av en maskin, må delene velges tilfeldig, men fra batcher produsert på forskjellige tidspunkter av dagen, eller på forskjellige dager eller uker..
Enkel tilfeldig prøvetaking:
- Det gjør det mulig å redusere kostnadene ved en statistisk studie, siden det ikke er nødvendig å studere den totale befolkningen for å oppnå statistisk pålitelige resultater, med ønsket konfidensnivå og feilnivået som kreves i studien..
- Unngå skjevhet: ettersom valget av elementene som skal studeres er helt tilfeldig, gjenspeiler studien trofast egenskapene til befolkningen, selv om bare en del av den ble studert.
- Metoden er ikke tilstrekkelig i tilfeller der du vil vite preferansene i forskjellige grupper eller populasjonslag.
I dette tilfellet er det å foretrekke å tidligere bestemme gruppene eller segmentene som studien skal utføres på. Når lagene eller gruppene er definert, hvis det er hensiktsmessig å bruke tilfeldig prøvetaking på hver enkelt av dem..
- Det er svært lite sannsynlig at informasjon vil bli innhentet om minoritetssektorer, hvor det noen ganger er nødvendig å kjenne til deres egenskaper.
For eksempel, hvis det er et spørsmål om å lage en kampanje på et dyrt produkt, er det nødvendig å kjenne preferansene til de rikeste minoritetssektorene.
Vi ønsker å studere befolkningens preferanse for en bestemt coladrikk, men det er ingen tidligere undersøkelser i denne populasjonen, hvor størrelsen ikke er kjent..
På den annen side må prøven være representativ med et minimum konfidensnivå på 90% og konklusjonene må ha en prosentvis feil på 2%..
-Hvordan bestemme prøvestørrelsen n?
-Hva ville utvalgsstørrelsen være hvis feilmarginen blir avslappet til 5%??
Siden populasjonsstørrelsen er ukjent, brukes formelen ovenfor for å bestemme prøvestørrelsen:
n = (Ztop q) / (E.to)
Vi antar at det er like sannsynlighet for preferanse (p) for vårt brusmerke som for ikke-preferanse (q), så p = q = 0,5.
På den annen side, da resultatet av studien må ha en prosentvis feil mindre enn 2%, vil den relative feilen E være 0,02.
Til slutt produserer en Z-verdi = 1645 et konfidensnivå på 90%.
Oppsummert har vi følgende verdier:
Z = 1.645
p = 0,5
q = 0,5
E = 0,02
Med disse dataene beregnes den minste prøvestørrelsen:
n = (1.645to 0,5 0,5) / (0,02to) = 1691,3
Dette betyr at studien med ønsket feilmargin og med valgt nivå av tillit må ha et utvalg av respondenter på minst 1692 individer, valgt ved enkel tilfeldig prøvetaking..
Hvis du går fra en feilmargin på 2% til 5%, er den nye prøvestørrelsen:
n = (1.645to 0,5 0,5) / (0,05to) = 271
Noe som er et betydelig lavere antall individer. Avslutningsvis er utvalgsstørrelsen veldig følsom for ønsket feilmargin i studien..
Ingen har kommentert denne artikkelen ennå.