
Reynolds nummererer hva det er til, hvordan det beregnes, øvelser
De Reynolds nummer (Rog) er en dimensjonsløs numerisk størrelse som etablerer forholdet mellom treghetskreftene og de viskøse kreftene til en væske i bevegelse. Treghetskrefter bestemmes av Newtons andre lov og er ansvarlig for maksimal akselerasjon av væsken. Viskøse krefter er kreftene som motarbeider væskens bevegelse.
Reynolds-nummeret gjelder alle typer væskestrømmer, for eksempel strømning i sirkulære eller ikke-sirkulære kanaler, i åpne kanaler og strømning rundt nedsenkede legemer..
Verdien av Reynolds-tallet avhenger av tettheten, viskositeten, hastigheten på væsken og dimensjonene til strømbanen. Væskens oppførsel som en funksjon av mengden energi som blir spredt på grunn av friksjon, vil avhenge av om strømningen er laminær, turbulent eller mellomliggende. Av denne grunn er det nødvendig å finne en måte å bestemme typen flyt.
En måte å bestemme dette på er ved hjelp av eksperimentelle metoder, men de krever mye presisjon i målingene. En annen måte å bestemme flytstrømmen på er å skaffe Reynolds-nummeret.
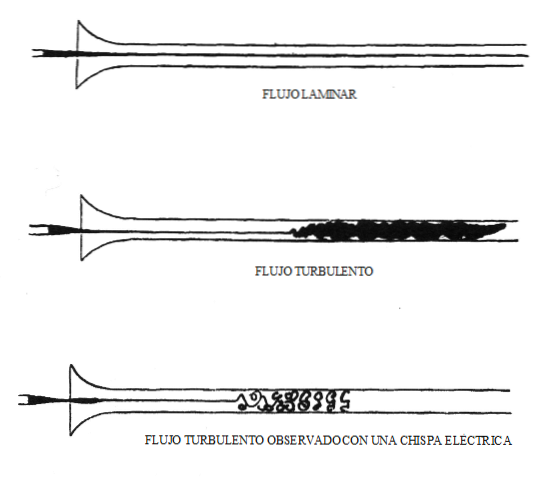
I 1883 oppdaget Osborne Reynolds at hvis verdien til dette dimensjonsløse tallet er kjent, kan den typen flyt som karakteriserer enhver situasjon med væskeledning, forutsies..
Artikkelindeks
- 1 Hva er Reynolds-tallet for?
- 2 Hvordan beregnes det?
- 3 Løst øvelser
- 3.1 Reynolds-nummer i en sirkulær kanal
- 3.2 Reynolds-nummer i en rektangulær kanal
- 3.3 Reynolds antall kule nedsenket i en væske
- 4 Søknader
- 4.1 Søknader i biologi
- 5 Referanser
Hva er Reynolds-tallet for?
Reynolds-tallet brukes til å bestemme oppførselen til en væske, det vil si for å bestemme om strømmen av en væske er laminær eller turbulent. Strømmen er laminær når de viskøse kreftene, som motsetter bevegelsen av væsken, er de som dominerer, og væsken beveger seg med tilstrekkelig liten hastighet og i en rettlinjet bane.
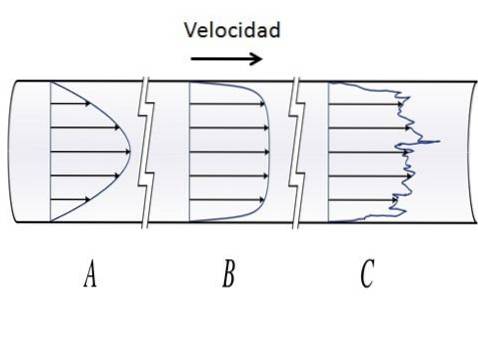
Væsken med laminær strøm oppfører seg som om det var uendelige lag som glir over hverandre på en ordnet måte uten blanding. I sirkulære kanaler har den laminære strømmen en parabolsk hastighetsprofil, med maksimale verdier i midten av kanalen og minimumsverdier i lagene nær kanaloverflaten. Verdien av Reynolds-tallet i laminær strømning er Rog<2000.
Strømmen er turbulent når treghetskreftene er dominerende og væsken beveger seg med svingende hastighetsendringer og uregelmessige baner. Turbulent strømning er veldig ustabil og viser momentumoverføringer mellom væskepartikler.
Når væsken sirkulerer i en sirkulær kanal, med turbulent strømning, krysser lagene av væske hverandre og danner virvler, og deres bevegelse har en tendens til å være kaotisk. Reynolds-tallverdien for turbulent strømning i en sirkulær kanal er Rog > 4000.
Overgangen mellom laminær strømning og turbulent strømning skjer for Reynolds tallverdier mellom 2000 Y 4000.
Hvordan beregnes det?
Ligningen som brukes til å beregne Reynolds-tallet i en kanal med sirkulært tverrsnitt er:
Rog = ρVD / η
ρ = Væsketetthet (kg / m3)
V = Strømningshastighet (m3/ s)
D = Karakteristisk lineær dimensjon av fluidbanen, som for tilfellet med den sirkulære kanalen representerer diameteren.
η = dynamisk viskositet av væsken (Pa.s)
Forholdet mellom viskositet og tetthet er definert som kinematisk viskositet v = η / ρ, og enheten er mto/ s.
Ligningen til Reynolds-tallet som en funksjon av kinematisk viskositet er:
Rog = VD / v
I kanaler og kanaler med ikke-sirkulære tverrsnitt er den karakteristiske dimensjonen kjent som hydraulisk diameter DH y representerer en generalisert dimensjon av væskebanen.
Den generaliserte ligningen for å beregne Reynolds-tallet i ledninger med ikke-sirkulære tverrsnitt er:
Rog = ρV 'DH / η
V '= Gjennomsnittlig strømningshastighet =GÅR
Hydraulisk diameter DH etablerer forholdet mellom området TIL av strømnings-tverrsnitt og fuktet omkrets PM .
DH = 4A / PM
Den våte omkretsen PM er summen av lengdene på kanalens vegger, eller kanalen, som er i kontakt med væsken.
Du kan også beregne Reynolds-tallet til en væske som omgir et objekt. For eksempel en kule nedsenket i en væske som beveger seg med hastighet V. Sfæren opplever en dragkraft FR definert av Stokes-ligningen.
FR = 6πRVη
R = kuleens radius
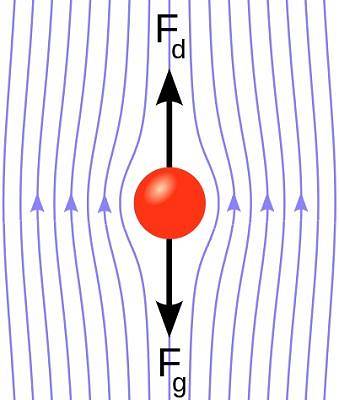
Reynolds-nummeret til en kule med hastighet V nedsenket i en væske er:
Rog = ρV R / η
Rog<1 cuando el flujo es laminar y Rog > 1 når strømningen er turbulent.
Løst øvelser
Følgende er tre Reynolds antall applikasjonsøvelser: Sirkulær kanal, Rektangulær kanal og sfære nedsenket i en væske.
Reynolds nummer i en sirkulær kanal
Beregn Reynolds antall propylenglykol a 20 °C i en sirkulær kanal med diameter 0,5 cm. Strømningshastigheten er 0,15 meter3/ s. Hva er typen flyt?
D =0,5 cm = 5.10-3m (karakteristisk dimensjon)
Væsketetthet er ρ = 1 036 g / cm3= 1036 kg / m3
Viskositeten til væsken er η = 0,042 Pa s = 0,042 kg / m.s
Strømningshastighet er V = 0,15 meter3/ s
Reynolds-tallligningen brukes i en sirkulær kanal.
Rog =ρDU/η
Rog = (1036 kg / m3x0,15m3/ s x 5.10-3m) /(0,042 kg / m.s) = 18,5
Strømmen er laminær fordi verdien av Reynolds-tallet er lav i forhold til forholdet Rog<2000
Reynolds nummer i en rektangulær kanal
Bestem typen flyt av etanolen som flyter med en hastighet på 25 ml / min i et rektangulært rør. Dimensjonene på den rektangulære seksjonen er 0,5 cm og 0,8 cm.
Tetthet ρ = 789 kg / m3
Dynamisk viskositet η = 1.074 mPa s = 1.074,10-3 kg / m.s
Først bestemmer du gjennomsnittlig strømningshastighet.
V ' =GÅR
V = 25 ml / min = 4.16.10-7m3/ s
Tverrsnittet er rektangulært hvis sider er 0,005m og 0,008m. Tverrsnittsområdet er A = 0,005m x0,008m = 4,10-5mto
V ' = (4.16.10-7m3/ s) / (4.10-5mto) = 1,04 × 10-tom / s
Den fuktede omkretsen er summen av sidene av rektangelet.
PM=0,013m
Den hydrauliske diameteren er DH = 4A / PM
DH = 4 × 4,10-5mto/ 0,013m
DH= 1.23.10-tom
Reynolds-tallet er hentet fra ligningen Rog = ρV 'DH / η
Rog = (789 kg / m3x1,04 × 10-tom / s x1.23.10-tom) / 1.074,10-3 kg / m.s
Rog = 93974
Strømmen er turbulent fordi Reynolds-tallet er veldig stort (Rog> 2000)
Reynolds nummer av en kule nedsenket i en væske
En sfærisk latex polystyrenpartikkel med en radius på R= 2000 nm kastes vertikalt i vannet med en innledende størrelseshastighet V0= 10 m / s. Bestem Reynolds-nummeret til partikkelen nedsenket i vannet
Partikkeltetthet ρ = 1,04 g / cm3 = 1040 kg / m3
R= 2000nm = 0,000002m
Vanntetthet ρag= 1000 kg / m3
Viskositet η =0,001 kg / (m s)
Reynolds-tallet oppnås ved ligningen Rog = ρV R / η
Rog = (1000 kg / m3x10 m / s x 0,000002m) / 0,001 kg / (m s)
Rog = 20
Reynolds-tallet er 20. Strømmen er turbulent.
applikasjoner
Reynolds-nummeret spiller en viktig rolle i væskemekanikk og varmeoverføring fordi det er en av hovedparametrene som kjennetegner en væske. Noen av applikasjonene er nevnt nedenfor.
1-Det brukes til å simulere bevegelsen til organismer som beveger seg på flytende overflater, for eksempel: bakterier suspendert i vann som svømmer gjennom væsken og produserer tilfeldig agitasjon.
2-Den har praktiske anvendelser i strømmen av rør og i væskesirkulasjonskanaler, begrensede strømmer, spesielt i porøse medier.
3-I suspensjonene av faste partikler nedsenket i en væske og i emulsjoner.
4-Reynolds-nummeret brukes i vindtunneltester for å studere de aerodynamiske egenskapene til forskjellige overflater, spesielt når det gjelder flyreiser.
5-Den brukes til å modellere bevegelse av insekter i luften.
6-Utformingen av kjemiske reaktorer krever bruk av Reynolds-nummeret for å velge strømningsmodell med tanke på hodetap, energiforbruk og området for varmeoverføring..
7-I spådommen for varmeoverføring av elektroniske komponenter (1).
8-I prosessen med å vanne hagene og frukthagene der det er nødvendig å kjenne vannstrømmen som kommer ut av rørene. For å oppnå denne informasjonen bestemmes det hydrauliske hodetapet som er relatert til friksjonen mellom vannet og rørveggene. Trykkfallet beregnes når Reynolds-tallet er oppnådd.

Søknader i biologi
I biologi krever studiet av bevegelse av levende organismer gjennom vann, eller i væsker med egenskaper som ligner på vann, å oppnå Reynolds-tallet, som vil avhenge av størrelsen på organismer og hastigheten med hvilken de fortrenger.
Bakterier og encellede organismer har et veldig lavt Reynolds-antall (Rog<<1Strømmen har følgelig en laminær hastighetsprofil med overvekt av viskøse krefter.
Organismer med en størrelse nær maur (opptil 1 cm) har et Reynolds-nummer i størrelsesorden 1, som tilsvarer overgangsregimet der treghetskreftene som virker på organismen er like viktige som de viskøse kreftene i væsken.
I større organismer som mennesker er Reynolds-tallet veldig stort (Rog>> 1).
Referanser
- Anvendelse av lav-Reynolds antall turbulente strømningsmodeller for å forutsi elektronisk komponentvarmeoverføring. Rodgers, P og Eveloy, V. NV: s.n., 2004, IEEE, bind 1, s. 495-503.
- Mott, R L.. Anvendt væskemekanikk. Berkeley, CA: Pearson Prentice Hall, 2006, bind I.
- Collieu, A M og Powney, D J. De mekaniske og termiske egenskapene til materialer. New YorK: Crane Russak, 1973.
- Kay, J M og Nedderman, R M. En introduksjon til væskemekanikk og varmeoverføring. New York: Cambridge Universitty Press, 1974.
- Happel, J og Brenner, H. Væskemekanikk og transportprosesser. Hingham, MA: MartinusS Nijhoff Publishers, 1983.



Ingen har kommentert denne artikkelen ennå.