De lineære bølger er de der superposisjonsprinsippet er anvendelig, det vil si de der bølgeformen og dens romtidsutvikling kan oppnås som summen av grunnleggende løsninger, for eksempel av en harmonisk type. Ikke alle bølger overholder superposisjonsprinsippet, de som ikke overholder kalles ikke-lineære bølger.
Navnet "lineær" kommer fra det faktum at lineære bølger alltid tilfredsstiller en differensialligning i partielle derivater, der alle begrepene som involverer den avhengige variabelen eller dens derivater blir hevet til første kraft.
På den annen side tilfredsstiller ikke-lineære bølger bølgelikninger som har kvadratiske termer eller høyere grader i den avhengige variabelen eller i dens derivater.
Lineære bølger forveksles noen ganger med langsgående bølger, som er de der vibrasjonen oppstår i samme formeringsretning, som lydbølger.
Men langsgående bølger, så vel som tverrgående bølger, kan i sin tur være lineære eller ikke-lineære avhengig av blant annet amplituden til den opprinnelige forstyrrelsen og mediet de forplantes i..
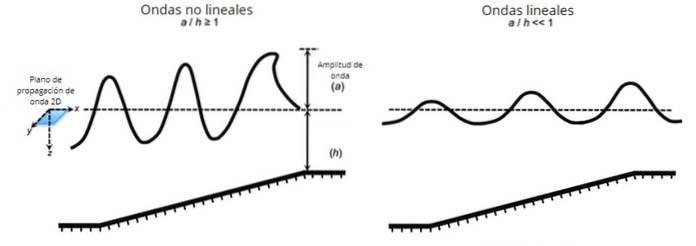
Det skjer generelt at når den opprinnelige forstyrrelsen er av liten amplitude, er ligningen som beskriver forplantningen av bølgen lineær eller kan lineæriseres av visse tilnærminger, selv om dette ikke alltid er tilfelle..
Artikkelindeks
I et lineært medium kan en bølgeform begrenset i rom og tid representeres av summen av bølgefunksjoner av sinus- eller cosinustypen av forskjellige frekvenser og bølgelengder ved bruk av Fourier-serier.
Lineære bølger har alltid assosiert med en differensialligning av den lineære typen, hvis løsning representerer forutsigelsen av hva forstyrrelsen vil være i senere øyeblikk av en innledende forstyrrelse lokalisert i begynnelsen.
Den klassiske lineære bølge ligningen, i en enkelt romlig dimensjon, hvis løsninger er lineære bølger er:
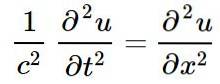
I ovenstående ligning eller representerer forstyrrelse av en viss fysisk størrelse på posisjonen x og i øyeblikket t, nemlig eller er en funksjon av x Y t:
u = u (x, t)
For eksempel hvis det er en lydbølge i luften, eller kan representere trykkets variasjon med hensyn til verdien uten å forstyrre.
Når det gjelder en elektromagnetisk bølge, representerer u det elektriske feltet eller magnetfeltet som svinger vinkelrett på forplantningsretningen.
I tilfelle et stramt tau, eller representerer den tverrgående forskyvningen i forhold til tauets likevektsposisjon, som vist i følgende figur:
Hvis det er to eller flere løsninger av den lineære differensiallikningen, vil hver løsning multiplisert med en konstant være en løsning, og det samme vil summen av dem.
I motsetning til ikke-lineære ligninger, tillater lineære bølgelikninger harmoniske løsninger av typen:
eller1= A⋅sen (k⋅x - ω⋅t) Y ellerto= A⋅sen (k⋅x + ω⋅t)
Dette kan verifiseres ved enkel erstatning i lineærbølgeligningen.
Den første løsningen representerer en vandrende bølge som beveger seg mot høyre, mens den andre løsningen til venstre raskt c = ω / k.
Harmoniske løsninger er karakteristiske for lineære bølger.
På den annen side er den lineære kombinasjonen av to harmoniske løsninger også en løsning av den lineære bølge ligningen, for eksempel:
u = A.1 cos (k1⋅x - ω1⋅t) + Ato sen (kto⋅x - ωto⋅t) er løsning.
Det mest relevante kjennetegnet ved lineære bølger er at enhver bølgeform, uansett hvor kompleks, kan oppnås gjennom en summering av enkle harmoniske bølger i sinus og cosinus:
u (x, t) = A0 + ∑n TILn cos (kn⋅x - ωn⋅t) + ∑m Bm sen (km⋅x - ωm⋅t).
I den klassiske lineære bølge ligningen, c representerer forplantningshastigheten til pulsen.
I tilfeller der c er en konstant verdi, for eksempel elektromagnetiske bølger i vakuum, deretter en puls i begynnelsen t = 0 Form f (x) sprer seg i henhold til:
u (x, t) = f (x - c⋅t)
Uten å lide noen forvrengning. Når dette skjer, sies det at mediet ikke er dispersivt..
I dispersivt medium kan forplantningshastigheten c imidlertid avhenge av bølgelengden λ, det vil si: c = c (λ).
Elektromagnetiske bølger er spredte når de beveger seg gjennom et materialmedium. Også vannets overflatebølger beveger seg i forskjellige hastigheter, avhengig av dybden på vannet.
Hastigheten som en harmonisk bølge av typen A⋅sen (k⋅x - ω⋅t) Det er ω / k = c y kalles fasehastigheten. Hvis mediet er spredt, da c er en funksjon av bølgetallet k: c = c (k), hvor k er relatert til bølgelengde av k = 2π / λ.
Forholdet mellom frekvens og bølgelengde kalles spredningsforhold, enn uttrykt i form av vinkelfrekvensen ω og bølgetallet k Det er: ω = c (k) ⋅k.
Noen karakteristiske spredningsforhold for lineære bølger er som følger:
I havbølger der bølgelengden (avstanden mellom toppene) er mye større enn dybden H, men siden amplituden er mye mindre enn dybden, er spredningsforholdet:
ω = √ (gH) ⋅k
Derfra konkluderes det at de formerer seg i konstant hastighet √ (gH) (ikke-spredt medium).
Men bølger i veldig dype farvann er spredte, siden spredningsforholdet er:
ω = √ (g / k) ⋅k
Dette betyr at fasehastigheten ω / k er variabel og avhenger av bølgetallet og derfor av bølgelengden til bølgen.
Hvis to harmoniske lineære bølger overlapper hverandre, men går frem med forskjellige hastigheter, stemmer ikke gruppehastigheten (det vil si bølgepakken) med fasehastigheten.
Gruppefart vg er definert som derivatet av frekvensen med hensyn til bølgetallet i dispersjonsforholdet: vg = ω '(k).
Figuren nedenfor viser superposisjonen eller summen av to harmoniske bølger eller1= A⋅sen (k1⋅x - ω1⋅t) Y ellerto= A⋅sen (kto⋅x - ωto⋅t) reiser i forskjellige hastigheter v1= ω1/ k1 Y vto= ωto/ kto. Legg merke til hvordan gruppehastigheten er forskjellig fra fasehastigheten, i dette tilfellet er gruppehastigheten ∆ω / ∆k.
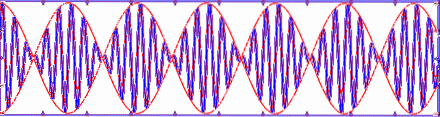
Avhengig av dispersjonsforholdet, kan det til og med skje at fasehastigheten og gruppehastigheten i lineære bølger har motsatt retning..
Elektromagnetiske bølger er lineære bølger. Dens bølgeligning er avledet fra ligningene til elektromagnetisme (Maxwells ligninger) som også er lineære.
Det er ligningen som beskriver dynamikken til partiklene på en atomskala, der bølgeegenskapene er relevante, for eksempel tilfellet med elektroner i atomet.
Så "elektronbølgen" eller bølgefunksjonen som den også kalles, er en lineær bølge.
Lineære bølger er også de hvor amplituden er mye mindre enn bølgelengden og bølgelengden mye større enn dybden. Bølger på dypt vann følger den lineære teorien (kjent som Airy wave theory).
Imidlertid er bølgen som nærmer seg kysten og danner den karakteristiske krøllkammen (og som surfere elsker) en ikke-lineær bølge..
Siden lyd er en liten forstyrrelse av atmosfæretrykket, regnes det som en lineær bølge. Sjokkbølgen fra en eksplosjon eller bølgefronten fra et supersonisk fly er imidlertid typiske eksempler på en ikke-lineær bølge..
Bølgene som forplanter seg gjennom et stramt tau er lineære, så lenge den første pulsasjonen er av liten amplitude, det vil si at den elastiske grensen til tauet ikke overskrides..
Lineære bølger i strengene reflekteres i endene og overlapper hverandre, noe som gir opphav til stående bølger eller vibrasjonsmodus som gir harmoniske og subharmoniske toner som er karakteristiske for strykeinstrumenter..
Ingen har kommentert denne artikkelen ennå.