De er tredimensjonale bølger de som forplanter seg i rommet, for eksempel lydbølgen produsert av en høyttaler. Denne bølgen forplanter seg i alle retninger, men ikke med samme intensitet i dem alle..
Hvis en forstyrrelse oppstår på et punkt i rommet, forplantes den i de tre romlige retningene, bølgefrontene er lukkede overflater, sfæriske, elliptiske eller av en annen type..
På den annen side, hvis stedet der bølgene stammer, det vil si kilden, har en flat fordeling, vil forstyrrelsen hovedsakelig bevege seg i retningen vinkelrett på nevnte plan og danne flate bølgefronter..
Artikkelindeks
I tredimensjonale bølger er bølgefronter et sett med overflater nedsenket i et tredimensjonalt rom.
Nå er bølgefronten stedet for punktene i rommet som nås av den opprinnelige forstyrrelsen, på samme øyeblikk..
Det regnes vanligvis som tre typer bølger som beveger seg i et tredimensjonalt rom, i henhold til symmetrien til bølgefronten: planbølger, sylindriske bølger og sfæriske bølger. Imidlertid tilhører ikke virkelige bølger alltid disse typene, fordi de ikke har så høy grad av symmetri.
En plan bølge som beveger seg i positiv x-retning med hastighet v, er funksjonelt representert som:
g (x, t) = f (x - v⋅t)
Denne bølgen er ikke begrenset til aksen x, den strekker seg også i retningene Y Y z. Men den funksjonelle formen forteller oss at alle punkter som har samme x-koordinat, uavhengig av koordinatene (z, y), har samme g-verdi.
I dette tilfellet er bølgefronter plan parallelt med z-y-planet som beveger seg raskt v, som betyr at planbølgen opptar alt tredimensjonalt rom.
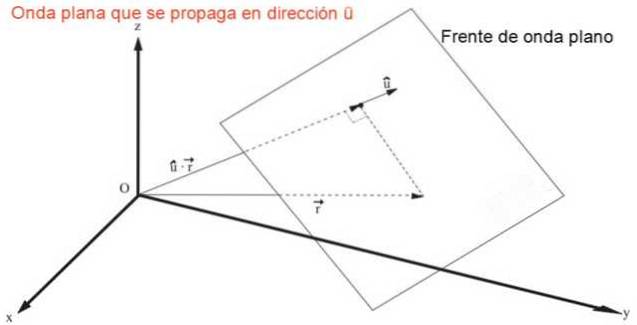
Uttrykket som representerer en plan bølge som forplanter seg i hvilken som helst retning eller raskt v, hvor eller representerer en enhetsvektor av regissorkosinus cos (α), cos (β) Y cos (γ), Det er:
g = f (û • r - v⋅t) = f (x cos (α) + y cos (β) + z cos (γ) - v⋅t)
Det er lett å vise, ved direkte erstatning, at det forrige uttrykket er en løsning av den tredimensjonale bølgelikningen, en ligning i delvis derivater av den andre lineære orden:
∂xxg + ∂yyg + ∂zzg = (1 / vto) ∂ttg
Ovennevnte ligning kan skrives mer kompakt ved hjelp av Laplacian-operatoren ∇to:
∇tog = (1 / vto) ∂ttg
Når den opprinnelige forstyrrelsen fordeles over en rett linje, forplantes bølgen i radiell retning vinkelrett på den linjen, og fyller det tredimensjonale rommet som omgir den, med sylindriske bølgefronter..
Når kilden er punkt og mediet der den tredimensjonale bølgen forplanter seg er homogen og isotrop (egenskapene endres ikke i henhold til retningen), så er bølgefrontene sfærer konsentriske til det punktet der den opprinnelige forstyrrelsen skjedde..
I tilfelle en sfærisk bølge der intensiteten til bølgen er identisk i alle retninger, avhenger funksjonen som beskriver forstyrrelsen bare avstanden r til punktkilden og tiden t.
I dette tilfellet har vi at den tilsvarende laplacianen er:
∇tog = (1 / rto) ∂r(rto ∂rg)
Å være bølge ligningen:
∇tog = (1 / vto) ∂ttg
Den generelle løsningen vil være:
g (r, t) = (1 / r) F (r - v⋅t) + (1 / r) G (r + v⋅t)
I dette tilfellet sies det at det er en sfærisk bølge. Men det kan være varianter, som det vil sees nedenfor
Det kan også skje at en sfærisk bølge, det vil si med bølgefronter dannet av sfærer konsentrisk til et sentralt punkt, er amplituden eller intensiteten til bølgen forskjellig i de forskjellige retningene..
Dette er hva som skjer når den sentrale kilden til bølgen er mer effektiv i en retning enn andre..
For eksempel har ikke lyden som produseres av en høyttaler den samme intensiteten overalt, selv ikke på punkter som er like langt fra høyttaleren..
Intensiteten er ikke den samme selv om signalet tar samme tid å nå disse punktene. Det er en sfærisk bølge som har et ikke-sfærisk retningsmønster.
Du har også sfæriske bølger når det gjelder elektromagnetiske bølger opprettet av en antenne, men de er kanskje ikke like sterke i alle retninger..
Når mediet er inhomogent, er hastigheten på forplantningen av bølgen forskjellig i forskjellige retninger.
Et eksempel på et inhomogent medium er atmosfæren der det er trykkforskjeller med høyden og det er temperaturgradienter. Et annet eksempel er lag av jordskorpen, som avviker i tetthet og elastisk modul..
Ikke-homogeniteten resulterer i at bølgefronter som stammer fra en sentral punktkilde ikke er konsentriske sfærer, siden bølgen i samme tidsperiode er forskjellig i hver retning..
Så har vi en tredimensjonal bølge hvis bølgefront ikke er sfærisk.
Vi kan skrive uttrykket av en sfærisk harmonisk bølge slik:
g (r, t) = (geller / r) cos (k⋅r - ω⋅t)
Der bølgefrontene forplanter seg med radiell hastighet lik:
v = ω / k
Og amplituden reduseres med det inverse avstanden r fra punktkilden til sfæriske bølger.
Harmoniske bølger har energi tetthet (energi per volumsenhet) ε gitt av:
ε = ½ ρ ωto (geller / r)to
I denne ligningen:
-ρ har masseenheter per volumenhet og representerer tettheten til mediet der en lydbølge forplanter seg.
-geller er amplituden til forskyvningen av et element i mediet, for eksempel et fluid, på grunn av forplantningsbølgen.
Det skal bemerkes at, siden det er en sfærisk bølge, reduseres energitettheten med det inverse av kvadratet til avstanden.
Intensiteten til bølgen, det vil si overført energi per tidsenhet er:
I = v⋅ε
Som alltid er den viktigste mengden i praksis den overførte kraften per arealenhet på radiell avstand. r:
P = v⋅ε = Ieller / rto
Å være Jegeller = ½ ρ v ωto gellerto.
Den totale energien som overføres per tidsenhet gjennom en sfære med radius r er: P⋅4πrto= 4π⋅Ieller, og som forventet avhenger det ikke av den radiale avstanden.
Tredimensjonale bølger er veldig hyppige, så vi har:
De dekker et veldig bredt spekter, fra radiobølger mellom hundrevis av KHz og hundrevis av MHz, til bølgene som sendes ut av antennen til Wifi i størrelsesorden GHz, som allerede faller i mikrobølgeovnsområdet.
Vi vet at mikrobølger, selv om de ikke er ioniserende, kan øke kroppens temperatur fordi den inneholder mye vann.
Derfor anbefales det ikke å ha wi-fi-antennen nær hodet eller kroppen. Det er nok å bevege seg litt bort, siden intensiteten er på dobbelt avstand den fjerde delen.
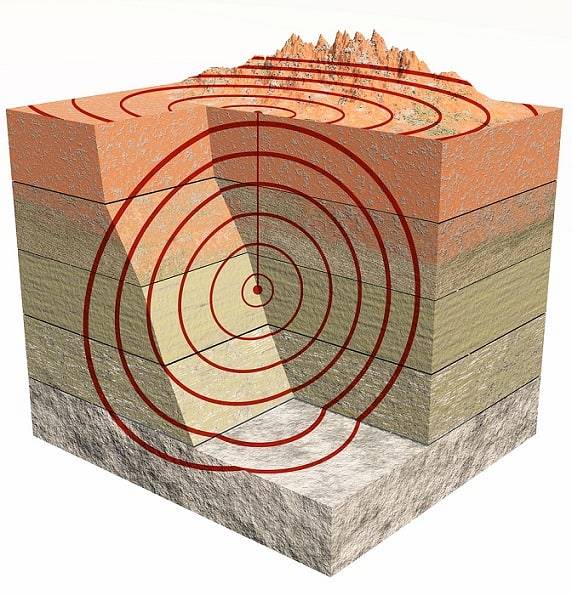
De er også tredimensjonale bølger. Hovedsakelig er det typen P hva er kompresjonsbølger og de av typen S som er skjæring eller skjæring (shøre på engelsk).
Bølgene P eller primær er de første som ankommer fordi de formerer seg raskere enn bølger S eller sekundær.
Lyd er en type tredimensjonal bølge. Disse bølgene forplanter seg i alle retninger, selv om, som vi har sagt tidligere, ikke med samme intensitet i alle retninger..
Dette er fordi lydkilden ikke alltid avgir perfekt sfærisk symmetri.
Ingen har kommentert denne artikkelen ennå.