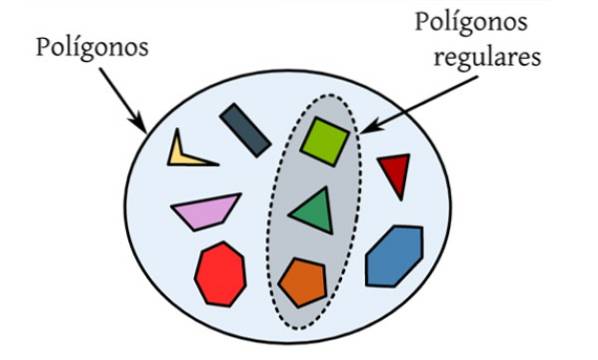
De vanlige polygoner er de som har alle sine sider og deres indre vinkler like. I den følgende figuren er det et sett med forskjellige polygoner, som er plane figurer begrenset av en lukket kurve, og bare de som er uthevet oppfyller betingelsene for å være regelmessige.
For eksempel er den ligesidige trekanten en vanlig polygon, siden de tre sidene måler det samme, så vel som de indre vinklene, som er verdt 60 ° hver..
Firkanten er en firkant med fire sider av like mål og hvis indre vinkler er 90º. Den følges av den vanlige femkant, med fem sider av samme størrelse og fem indre vinkler på hver 108 °..
Når en polygon er vanlig, blir dette ordet lagt til det spesielle navnet, så vi har den vanlige sekskanten, den vanlige heptagonen og så videre.
Artikkelindeks
De viktigste egenskapene til vanlige polygoner kan oppsummeres som følger:
-Sidene måler det samme, derfor er de likesidig.
-De er ekvivalent, siden alle dens indre vinkler har samme mål.
-De kan alltid skrives inn i en omkrets, noe som betyr at de passer perfekt innenfor en, som kalles begrenset omkrets.
-For en vanlig polygon med n sider er målingen på en indre vinkel α:
α = [180 (n-2)] / n
-Du kan tegne n (n-3) / 2 diagonaler fra toppunktene på en polygon, enten det er vanlig eller ikke.
-Summen av utvendige vinkler er lik 360º.
Deretter presenterer vi hovedelementene i en vanlig polygon, visualisert i figuren nedenfor.
Felles poeng som to påfølgende sider har, betegnet som V i figuren.
Det er segmentet som forbinder to påfølgende hjørner av polygonet og er betegnet som ℓ eller L.
Segment som forbinder to ikke-påfølgende hjørner av polygonet, i figuren er det betegnet som d.
Det er det felles sentrum for den innskrevne sirkelen og den omskrevne sirkelen, betegnet med bokstaven O. Det kan også sees på som det eneste punktet som er like langt fra både toppunktene og midtpunktene på hver side..
Det er radioen r av den omskrevne sirkelen og sammenfaller med avstanden mellom O og et toppunkt.
Det kalles apotem til radiusen av omkretsen innskrevet i polygonet, representert i figuren med en bokstav til. Apotemet er vinkelrett på den ene siden og forbinder det med sentrum O (rødt segment i figur 3).
Å kjenne radiusen r og lengden på siden, beregnes apotemet av:
Siden apotemet faktisk er et av bena til en høyre trekant (se figur 3), er det andre benet verdien av ℓ / 2 (halvparten av en side) og hypotenusen radius r av polygonen.
Når Pythagoras-teoremet brukes på nevnte trekant, oppnås denne ligningen, som ikke bare er gyldig for sekskanten, men for enhver vanlig polygon.
Det er vinkelen hvis toppunkt faller sammen med sentrum O, og hvis sider er segmentene som forbinder sentrum med to påfølgende hjørner. Dens mål i seksagesimale grader er 360º / n, hvor n er antall sider av polygonet.
Det er forskjellen mellom polygonens og apotemets radius (se figur 3). Betegner sagitta som S:
S = r - a
Det beregnes enkelt ved å legge til lengden på sidene. Siden en hvilken som helst side har like lengde L og det er n sider, blir omkretsen P uttrykt som:
P = n.L
I en vanlig polygon er området A gitt av produktet mellom den halve omkretsen (halvparten av omkretsen) og lengden på apotemet til.
A = P.a / 2
Siden omkretsen avhenger av antall sider n, viser det seg at:
A = (nL) .a / 2
To vanlige polygoner kan ha samme omkrets selv om de ikke har like mange sider, siden det da vil avhenge av lengden på sidene.
I bok V av hans Samling, matematikeren Pappus fra Alexandria (290-350), den siste av de store antikke greske matematikerne, viste at blant alle de vanlige polygoner med samme omkrets er den med det største området den som har flest sider.
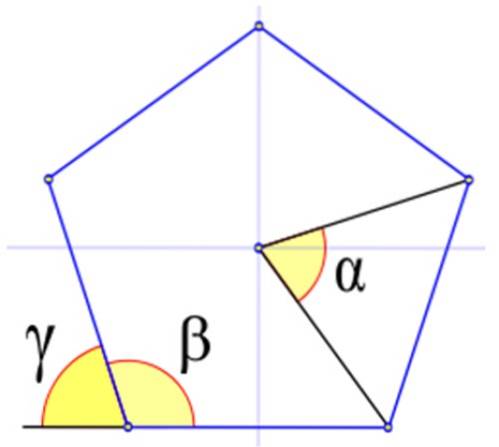
Figur 4 viser de relevante vinklene i en vanlig polygon, betegnet med de greske bokstavene α, β og γ.
Tidligere nevnte vi den sentrale vinkelen, mellom elementene i den vanlige polygonen, det er vinkelen hvis toppunkt er i midten av polygonen, og sidene er segmentene som forbinder sentrum med to påfølgende hjørner.
For å beregne målet på den sentrale vinkelen α, del 360º med n, antall sider. Eller 2π radianer mellom n:
α = 360º / n
Tilsvarer i radianer til:
α = 2π / n
I figur 4 er den indre vinkelen β den som toppunktet sammenfaller med en av figuren, og dens sider er også sider av figuren. Det beregnes i seksagesimale grader av:
β = [180 (n-2)] / n
Eller i radianer ved bruk av:
β = [π (n-2)] / n
De er betegnet med den greske bokstaven γ. Figuren viser at γ + β = 180º. Derfor:
γ = 180º - β
Summen av alle de ytre vinklene til en vanlig polygon er 360º.
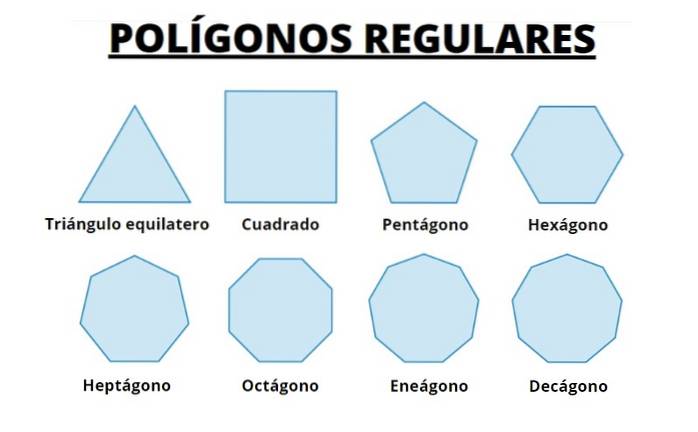
Deretter har vi de første 8 vanlige polygoner. Vi observerer at når antall sider øker, ligner polygonen i økende grad omkretsen de er innskrevet i.
Vi kan forestille oss at ved å gjøre lengden på sidene mindre og mindre, og øke antallet av disse, får vi omkretsen.
Vanlige polygoner finnes overalt i hverdagen og til og med i naturen. La oss se på noen eksempler:
Vanlige polygoner som ensidige trekanter, firkanter og romber florerer i skiltingen vi ser på motorveier og veier. I figur 6 ser vi et stoppskilt med en åttekantet form.
Utallige møbler har torget, for eksempel som sin karakteristiske geometriske figur, like mange bord, stoler og benker er firkantede. En parallelepiped er vanligvis en boks med sider i form av et rektangel (som ikke er en vanlig polygon), men de kan også gjøres firkantede..
Flisene på gulv og vegger, både i hjemmene og på gatene, er ofte formet som vanlige polygoner..
Tessellasjoner er overflater dekket helt med fliser som har forskjellige geometriske former. Med trekanten, firkanten og sekskanten kan du lage regelmessige tessellasjoner, de som bare bruker en enkelt type figur for å dekke perfekt, uten å etterlate tomme mellomrom (se figur 6).
På samme måte bruker bygninger vanlige polygoner i elementer som vinduer og dekor..
Overraskende nok er den vanlige sekskanten en polygon som vises ofte i naturen..
Kammene laget av bier for å lagre honning er formet veldig nær en vanlig sekskant. Som Pappus fra Alexandria observerte, på denne måten optimaliserer biene plassen for å lagre så mye honning som mulig..
Og det er også vanlige sekskanter i skilpaddeskallet og snøfnuggene, som også adopterer forskjellige veldig vakre geometriske former..
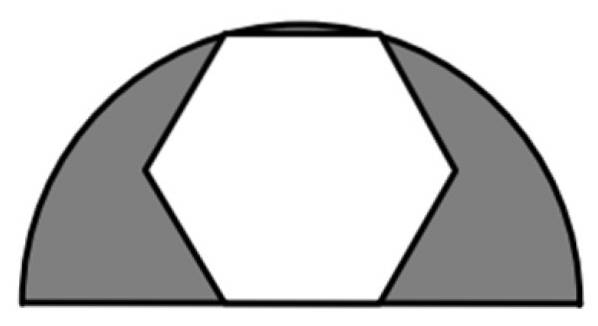
En vanlig sekskant er innskrevet i en halvcirkel med en radius på 6 cm, som vist på figuren. Hva er verdien av det skyggelagte området?
Det skyggelagte området er forskjellen mellom området til halvcirkelen med radien R = 6 cm og området til hele sekskanten, en vanlig 6-sidig polygon. Så vi trenger formler for området til hver av disse figurene.
TIL1 = π Rto / 2 = π (6 cm)to / 2 = 18π cmto
Formelen for å beregne arealet til en vanlig polygon er:
A = P.a / 2
Hvor P er omkretsen og til er apotemet. Siden omkretsen er summen av sidene, trenger vi verdien av disse. For den vanlige sekskanten:
P = 6ℓ
Derfor:
A = 6ℓa / 2
For å finne verdien av siden ℓ er det nødvendig å konstruere hjelpetall, som vi vil forklare nedenfor:
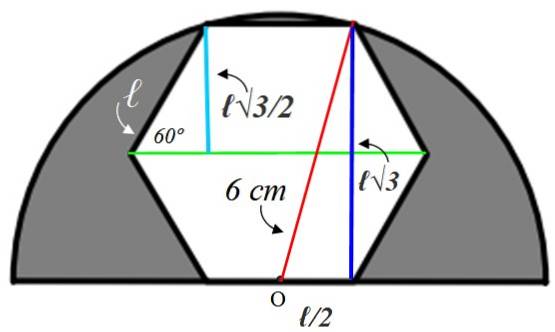
La oss starte med den lille høyre trekanten til venstre, hvis hypotenus er ℓ. En indre vinkel på sekskanten er lik:
α = [180 (n-2)] / n = α = [180 (6-2)] / 6 = 120º
Radien vi har tegnet i grønt halverer denne vinkelen, derfor er den spisse vinkelen til den lille trekanten 60º. Med den gitte informasjonen løses denne trekanten ved å finne den lyseblå siden, som måler det samme som apotemet:
Motsatt ben = a = ℓ x sin 60º = ℓ√3 / 2 cm
Denne verdien det er det dobbelte av det mørkeblå benet til den store trekanten til høyre, men fra denne trekanten vet vi at hypotenusen måler 6 cm fordi det er radiusen til halvcirkelen. Det gjenværende beinet (nederst) er lik ℓ / 2 siden punkt O er midt på siden.
Siden innvendige vinkler av denne trekanten ikke er kjent, kan vi si den pythagoriske teoremet for den:
36 = 3 ℓto + ℓto / 4
(13/4) ℓto = 36 → ℓ = √ (4 x36) / 13 cm = 12 / √13 cm
Med denne verdien beregnes apotemet:
a = ℓ√3 / 2 cm = (12 / √13) x (√3 / 2) cm = 6√3 / √13 cm
La oss ringeto til området til den vanlige sekskanten:
= 28,8 cmto
TIL1 - TILto = 18π cmto - 28,8 cmto = 27,7 cmto
Ingen har kommentert denne artikkelen ennå.