
Første likevektstilstandsforklaring, eksempler, øvelser
De første likevektstilstand krever at vektorsummen av alle kreftene som virker på en kropp er null, slik at den er i ro (statisk likevekt) eller med jevn rettlinjet bevegelse (dynamisk likevekt).
Denne summen av krefter er ingen ringere enn nettokraften som virker på kroppen, uttrykt matematisk på denne måten:
Fnett = 0
∑ F = 0

I rommet gir den første likevektstilstanden tre ligninger, en for hver dimensjon:
∑ Fx = 0; ∑ FY = 0 og ∑ Fz = 0
Når disse ligningene er oppfylt, oversettes ikke objektet, eller hvis det gjør det, vil det være med konstant hastighet.
Når vi ser rundt oss, innser vi at vi kontinuerlig prøver å tilfredsstille den første balansen, slik at ting ikke faller.
Derfor søker den å kompensere jordens gravitasjonsattraksjon ved hjelp av støtter, tau eller støtter av noen, slik at ting på denne måten forblir på plass og ikke havner på bakken..
Andre ganger er det som trengs å forhindre at eksterne elektromagnetiske felt forstyrrer driften av elektriske kretser og kommunikasjonsenheter. I dette tilfellet er det de elektriske ladningene som må være i likevekt..
Artikkelindeks
- 1 Eksempler
- 1.1 Bygninger
- 1.2 Trafikklys og hengende skilt
- 1.3 Ledere i elektrostatisk likevekt
- 1.4 Taklamper
- 1.5 Bøker og gjenstander på bord
- 1.6 Måling av viskositeten til en væske
- 2 trinn for å bruke den første likevektstilstanden
- 3 Løst øvelser
- 3.1 - Øvelse løst 1
- 3.2 - Øvelse løst 2
- 4 Interessante emner
- 5 Referanser
Eksempler
Et stort antall hverdagsobjekter tilfredsstiller den første likevektstilstanden, det gjelder å nøye observere:
Bygninger
Byggherrer søker stabilitet i konstruksjoner slik at brukerne forblir trygge. Målet med statikk er å studere forholdene for statisk likevekt i bygninger, broer, veier og alle slags strukturer..
Trafikklys og hengende skilt
Disse signalanordningene må forbli faste for å oppfylle sine funksjoner, derfor holdes de av kabler, stolper og stenger på en slik måte at den første likevektsbetingelsen er oppfylt..

Ledere i elektrostvekttoppleilighet
Når ledende materialer som kobber og andre metaller får en elektrisk ladning, blir elektrostatisk likevekt snart etablert og etterlater overflødig ladning på den ledende overflaten. Inne i det elektriske feltet er null.
Denne effekten brukes ofte til å isolere elektrisk og elektronisk utstyr fra eksterne felt ved å bruke det såkalte Faraday-buret. Buret er laget av ledende materiale og omgir utstyret som skal beskyttes.
Under stormer fungerer biler som Faraday-bur ved å beskytte beboerne mot elektriske støt..
Taklamper
I belysningssystemer, som pendellamper, brukes den første likevektstilstanden til å feste dem til taket, gulvet eller veggen.

Bøker og gjenstander på bord
Gjenstander plassert på bord og hyller oppfyller den første likevektstilstanden. Den normale kraften som støtten utøver på gjenstandene er ansvarlig for å kompensere vekten.
Måling av viskositeten til en væske
For å bestemme viskositeten til en væske, slippes en sfærisk gjenstand med kjent diameter inn i dens indre, og hastigheten vil avta på grunn av motstand. Kulehastigheten er konstant, og er dermed i dynamisk likevekt.
Jo høyere viskositeten til væsken er, desto lavere hastighet kulen beveger seg inn i.
Fremgangsmåte for å anvende den første likevektstilstanden
-Lag et frikroppsdiagram som viser alle kreftene som virker på kroppen (utelat de som kroppen utøver på andre).
-Velg et kartesisk koordinatsystem, og sørg for at kreftene så langt som mulig er plassert på hvilken som helst av aksene. Den positive retningen tas vanligvis i bevegelsesretningen eller en mulig bevegelse.
-Bestem de kartesiske komponentene til hver styrke.
-Å anvende Newtons andre lov for hver komponent, slik den ble etablert i begynnelsen, forblir således et ligningssystem.
-Løs ligningssystemet som ble reist i forrige trinn.
Løst øvelser
- Løst øvelse 1
Blokken av figuren, av masse m, den beveger seg nedoverbakke på det skråplanet i vinkel θ med konstant hastighet. Beregn verdien av koeffisienten for kinetisk friksjon μk, hvis massen av blokken er m = 5 kg og θ = 37º.

Løsning
Det første trinnet er å tegne frikroppsdiagrammet og velge et kartesisk koordinatsystem for å uttrykke hver kraft vektor. Kreftene som virker på blokken er:
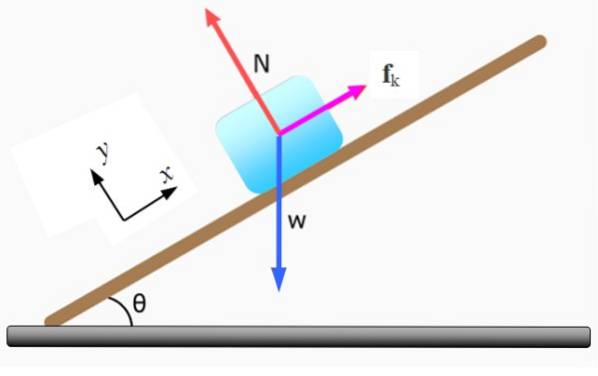
-Det normale N som utøves av det skråplanet, er vinkelrett på overflaten av dette.
-Vekten W er rettet vertikalt ned.
-Kinetisk friksjon Fk som er i motsetning til bevegelse. Hvis den ikke eksisterte, ville kroppen bevege seg nedoverbakke med en akselerasjon lik g.senθ.
Som vekt W er tilbøyelig i forhold til de valgte koordinataksene, må den spaltes i sine kartesiske komponenter:
Wx = mg sin 37º = 5 kg x 9,8 m / sto x sin 37º = 29. 5 N
WY = mg.kos 37º = 5 kg x 9,8 m / sto x cos 37º = 39,1 N
Newtons andre lov er nå brukt, og setter hver sum til 0, siden blokken mangler akselerasjon når den beveger seg med konstant hastighet:
∑ FY = N - WY = 0
∑ Fx = Wx - Fk = 0
Størrelsen på den kinetiske friksjonen er proporsjonal med størrelsen på det normale, og koeffisienten til den kinetiske friksjonen er μk konstanten av proporsjonalitet.
Fk = μk N
Samtidig:
N = WY = 39,1 N
I tillegg til:
Fk = Wx
Derfor:
- 5 N = μk x 39,1 N
μk = 29. 5 / 39,1 = 0,75
- Trening løst 2
Beregn størrelsen på spenningene som støtter trafikklyset med en vekt på 33 kg, vist i figuren:
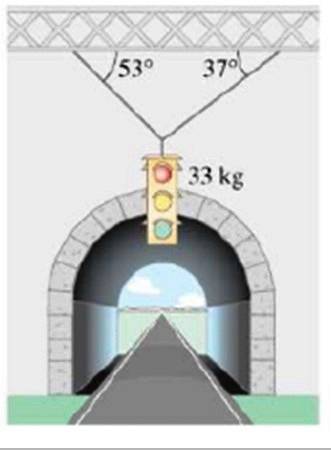
Løsning
Frikartdiagrammet er laget for både trafikklyset og knuten som holder kablene:
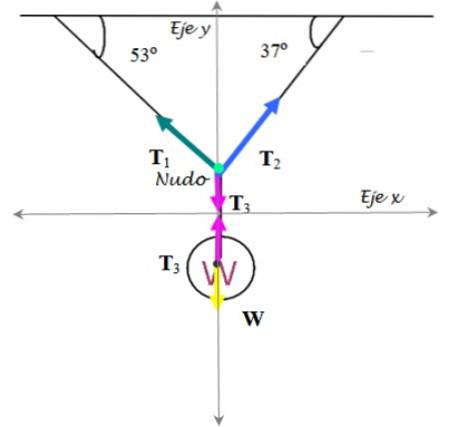
Trafikklys
På det handler: spenningen T3 opp og W vekt ned. Derfor:
∑ FY = W - T3 = 0
Derfor:
T3 = 33 kg x 9,8 m / sto = 323,4 N
Knute
Spenningene spaltes i deres kartesiske komponenter:
∑ FY = T1 sin 53º + Tto sen 37º - T3 = 0
∑ Fx = Tto cos 37º - T1 cos 53º = 0
Og følgende system med lineære ligninger oppnås med to ukjente T1 og Tto :
- 0,6 T1 + 0,8 Tto = 0
0,8 T1 + 0,6 Tto = 323,4
Løsningen på dette ligningssystemet er: T1 = 258,7 N og Tto = 194,0 N
Temaer av interesse
Likevektsforhold.
Andre likevektstilstand.
Referanser
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volum 4. Partikkelsystemer. Redigert av Douglas Figueroa (USB).
- Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. Sjette. Ed prentice hall.
- Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 1.
- Wikipedia. Statisk (mekanisk). Gjenopprettet fra: es.wikipedia.org.



Ingen har kommentert denne artikkelen ennå.