Heptagonale prismeegenskaper, volum, areal

EN heptagonalt prisme Det er en geometrisk figur som, som navnet antyder, involverer to geometriske definisjoner som er: prisme og heptagon. Et "prisme" er en geometrisk figur begrenset av to baser som er like og parallelle polygoner, og deres sideflater er parallellogrammer..

En "heptagon" er en polygon som består av syv (7) sider. Siden et heptagon er en polygon, kan det være vanlig eller uregelmessig.

En polygon sies å være regelmessig hvis alle sidene har samme lengde og dens indre vinkler måler den samme, de kalles også ligesidige polygoner; ellers sies det at polygonet er uregelmessig.

Kjennetegn ved et heptagonalt prisme

Nedenfor er visse egenskaper som et heptagonalt prisme har, for eksempel: dens konstruksjon, egenskaper til basene, arealet med alle ansiktene og volumet..

1- Konstruksjon

For å bygge et heptagonalt prisme, er to heptagoner nødvendige, som vil være dens baser og syv parallellogrammer, en for hver side av heptagonen..

Du begynner med å tegne en heptagon, så trekkes syv vertikale linjer, av samme lengde, som kommer ut fra hver av toppunktene.

Til slutt tegnes en annen heptagon slik at toppunktene sammenfaller med enden av linjene som er tegnet i forrige trinn..

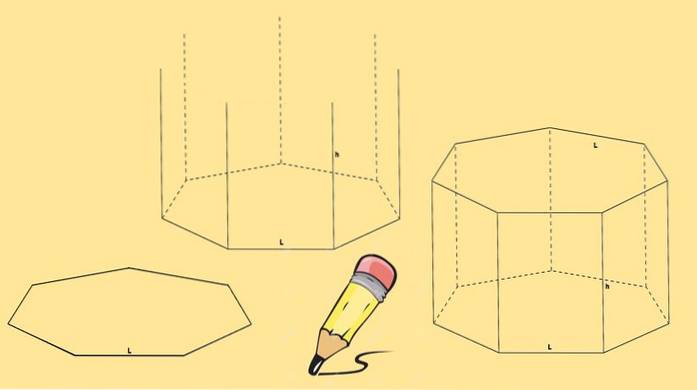
Det heptagonale prisme som er tegnet ovenfor kalles et høyre heptagonalt prisme. Men du kan også ha et skrått, heptagonalt prisme som i figuren nedenfor.

2 - Egenskapene til basene

Siden basene er heptagoner, tilfredsstiller de at det diagonale tallet er D = nx (n-3) / 2, hvor “n” er antall sider av polygonet; i dette tilfellet har vi D = 7 × 4/2 = 14.

Vi kan også se at summen av de interne vinklene til ethvert heptagon (vanlig eller uregelmessig) er lik 900º. Dette kan bekreftes av følgende bilde.

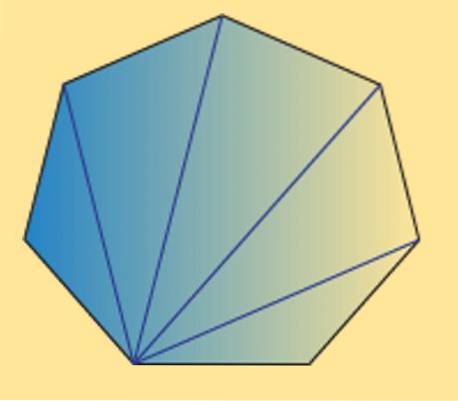
Som det fremgår er det 5 indre trekanter, og når summen av de indre vinklene til en trekant er lik 180 °, kan det oppnås at ønsket resultat.

3- Område som trengs for å bygge et heptagonalt prisme

Siden basene er to heptagoner og sidene er syv parallellogrammer, er området som trengs for å bygge et heptagonalt prisme lik 2xH + 7xP, hvor “H” er området til hver heptagon og “P” er området av hvert parallellogram..

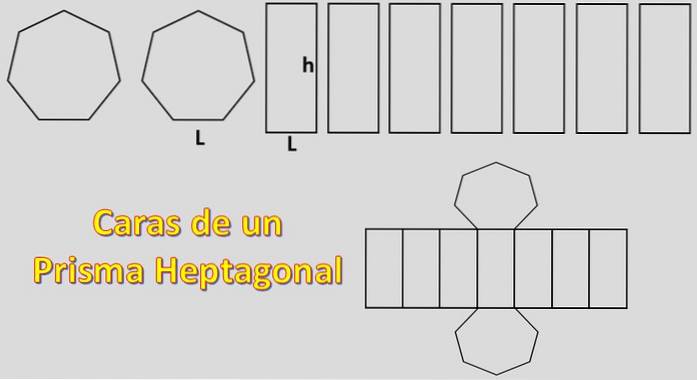
I dette tilfellet blir arealet til en vanlig heptagon beregnet. For dette er det viktig å vite definisjonen av apothem.

Apotemet er en vinkelrett linje som går fra midten av en vanlig polygon til midtpunktet på en av sidene.

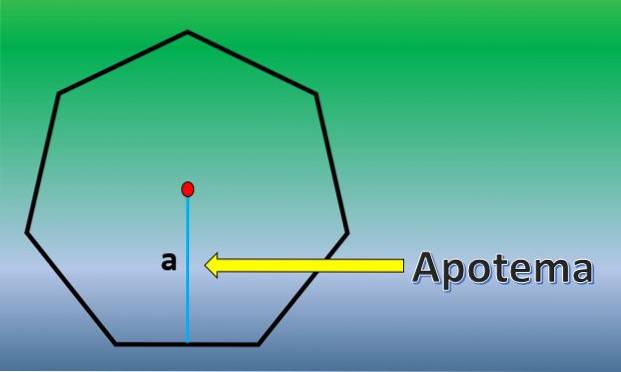
Når apotemet er kjent, er området til heptagonen H = 7xLxa / 2, hvor "L" er lengden på hver side og "a" er lengden på apotemet..

Arealet til et parallellogram er enkelt å beregne, det er definert som P = Lxh, der "L" har samme lengde som siden til heptagon og "h" er prismahøyden.

Avslutningsvis er mengden materiale som trengs for å bygge et heptagonalt prisme (med vanlige baser) 7xLxa + 7xLxh, det vil si 7xL (a + h).

4- Volum

Når området av en base og høyden på prismen er kjent, defineres volumet som (areal av basen) x (høyde).

I tilfelle av et heptagonalt prisme (med vanlig base) er volumet V = 7xLxaxh / 2; det kan også skrives som V = Pxaxh / 2, hvor "P" er omkretsen til det vanlige heptagonet.

Referanser

1. Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematikk: En problemløsningsmetode for lærere i grunnskolen. López Mateos Redaktører.
2. Fregoso, R. S. og Carrera, S. A. (2005). Matematikk 3. Redaksjonell Progreso.
3. Gallardo, G., og Pilar, P. M. (2005). Matematikk 6. Redaksjonell Progreso.
4. Gutiérrez, C. T. og Cisneros, M. P. (2005). Matematikkurs 3. Redaksjonell Progreso.
5. Kinsey, L. og Moore, T. E. (2006). Symmetri, form og rom: En introduksjon til matematikk gjennom geometri (illustrert, omtrykk red.). Springer Science & Business Media.
6. Mitchell, C. (1999). Blendende matematikklinjedesign (Illustrert utg.). Scholastic Inc..
7. R., M. P. (2005). Jeg tegner sjette. Redaksjonell Progreso.