I en isobarisk prosess, Presset P av et system forblir konstant. Prefikset "iso" kommer fra gresk og brukes til å betegne at noe forblir konstant, mens "baros", også fra gresk, betyr vekt.
Isobariske prosesser er veldig typiske både i lukkede containere og i åpne rom, og er enkle å lokalisere i naturen. Med dette mener vi at det er mulige fysiske og kjemiske endringer på jordoverflaten eller kjemiske reaksjoner i beholdere som er åpne for atmosfæren..
Noen eksempler er oppnådd ved å varme opp en ballong fylt med luft i solen, koke, koke eller fryse vann, damp generert i kjeler, eller prosessen med å heve en luftballong. Senere vil vi gi en forklaring på disse sakene.
Artikkelindeks
La oss utlede en ligning for den isobare prosessen forutsatt at systemet som studeres er en ideell gass, en modell som er ganske egnet for nesten hvilken som helst gass med mindre enn 3 atmosfærer av trykk. De ideelle gasspartiklene beveger seg tilfeldig og opptar hele volumet av rommet som inneholder dem uten å samhandle med hverandre..
Hvis den ideelle gassen som er innesluttet i en sylinder utstyrt med et bevegelig stempel, får ekspandere sakte, kan det antas at partiklene til enhver tid er i likevekt. Deretter utøver gassen på områdets stempel TIL en kraft F av størrelsesorden:
F = p.A
Hvor s er trykket fra gassen. Denne kraften utøver arbeid som produserer en uendelig liten forskyvning dx på stempelet gitt av:
dW = Fdx = pA.dx
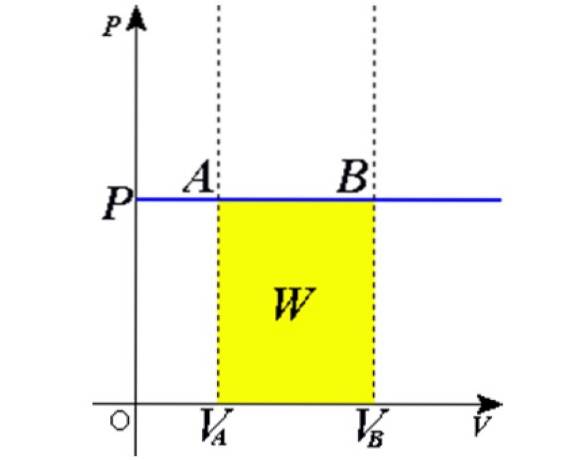
Som produktet Adx er en volumdifferensial dV, deretter dW = pdV. Det gjenstår å integrere begge sider fra det opprinnelige volumet VTIL til endelig volum VB for å få det totale arbeidet utført av gassen:
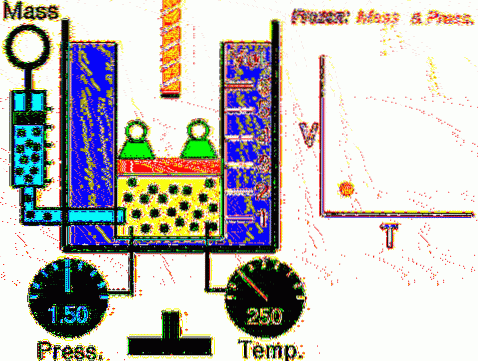
Den beskrevne situasjonen er eksperimentelt verifisert ved å begrense en gass inne i en sylinder forsynt med et bevegelig stempel, som vist i figur 2 og 3. En vekt av masse M er plassert på stempelet, hvis vekt er rettet nedover, mens gassen utøver en oppadgående kraft takket være trykket P produsert på stempelet.
Siden stempelet er i stand til å bevege seg fritt, kan volumet som gassen opptar endre seg uten problemer, men trykket forblir konstant. Legge til atmosfæretrykket Pminibank, som også utøver en nedadgående kraft, har vi:
Mg - P.A + Pminibank . A = konstant
Derfor: P = (Mg / A) + Pminibank det varierer ikke, med mindre M og dermed vekten endres. Ved å tilsette varme til sylinderen vil gassen utvide seg ved å øke volumet eller trekke seg sammen når den utvinner varme..
Den ideelle gassligningen for tilstanden relaterer variablene som er viktige: trykk P, volum V og temperatur T:
P.V = n .R.T
Her representerer n antall mol og R er den ideelle gasskonstanten (gyldig for alle gasser), som beregnes ved å multiplisere Boltzmanns konstant med Avogadros antall, noe som resulterer i:
R = 8,31 J / mol K
Når trykket er konstant, kan tilstandsligningen skrives som:
V / T = nR / P
Men nR / P er konstant, siden n, R og P er. Så når systemet går fra tilstand 1 til tilstand 2, oppstår følgende andel, også kjent som Charles lov:
V1/ T1 = Vto/ Tto
Bytte i W = PAV, arbeidet som er gjort for å gå fra tilstand 1 til tilstand 2 er oppnådd, i form av konstanter og temperaturvariasjon, lett å måle med et termometer:
W1 → 2 = nR (T.to - T1) = nR.ΔT
På den annen side sier termodynamikkens første lov at:
∆U = Q - W
Dette betyr at tilsetning av en viss mengde varme Q til gassen øker den indre energien ∆U og øker vibrasjonene i molekylene. På denne måten utvides gassen og fungerer ved å flytte stempelet, som vi har sagt før..
I en monatomisk ideell gass og variasjonen av den indre energien ∆U, som inkluderer både kinetisk energi og potensiell energi til molekylene, er:
∆U = (3/2)nR ΔT
Til slutt kombinerer vi uttrykkene vi har fått til ett:
Spørsmål = ∆U + W = (3/2)nR ΔT + nR∆T = (5/2) nR ΔT
Alternativt kan Q skrives om når det gjelder massen m, temperaturforskjellen og en ny konstant kalt spesifikk gassvarme ved konstant trykk, forkortet cs, hvis enheter er J / mol K:
Q = m cs ∆T
Ikke alle isobariske prosesser utføres i lukkede beholdere. Faktisk forekommer utallige termodynamiske prosesser av alle slag ved atmosfærisk trykk, så isobariske prosesser er veldig hyppige i naturen. Dette inkluderer fysiske og kjemiske endringer på jordoverflaten, kjemiske reaksjoner i karene som er åpne for atmosfæren og mye mer..
For at isobariske prosesser skal forekomme i lukkede systemer, må grensene deres være fleksible nok til å tillate volumendringer uten varierende trykk.
Dette skjedde i eksperimentet med stempelet som beveget seg lett når gassen utvidet seg. Det samme skjer ved å omslutte en gass i en festballong eller en luftballong.
Her har vi flere eksempler på isobariske prosesser:
Kokende vann til te eller kokesauser i åpne beholdere er gode eksempler på isobariske prosesser, siden de alle foregår ved atmosfærisk trykk..
Når vannet varmes opp, øker temperaturen og volumet, og hvis det fortsetter å tilsettes varme, er kokepunktet endelig nådd, hvor faseendringen av vannet fra væske til vanndamp oppstår. Mens dette skjer, forblir temperaturen også konstant ved 100 ° C..
På den annen side er frysing av vann også en isobarisk prosess, enten det foregår i en innsjø om vinteren eller hjemmekjøleskapet..
Et annet eksempel på en isobarisk prosess er endringen i volumet til en ballong som blåses opp med luft når den blir utsatt for solen. Først om morgenen, når den ikke er veldig varm ennå, har ballongen et visst volum..
Etter hvert som tiden går og temperaturen øker, varmes også ballongen opp og øker volumet og alt dette skjer ved konstant trykk. Ballongmaterialet er et godt eksempel på en kant som er fleksibel nok til at luften inni den utvides uten å endre trykket.
Opplevelsen kan også utføres ved å justere den ikke-oppblåste ballongen i tuten på en glassflaske fylt med en tredjedel vann, som varmes opp i en bain-marie. Så snart vannet er oppvarmet, blåses ballongen opp med en gang, men man må passe på å ikke varme for mye slik at den ikke eksploderer..
Det er et flytende skip uten fremdrift, som bruker luftstrømmer til å transportere mennesker og gjenstander. Ballongen er vanligvis fylt med varm luft, som, kaldere enn luften rundt, stiger og utvides og får ballongen til å stige..
Selv om luftstrømmene leder ballongen, har den brennere som aktiveres for å varme opp gassen når det er ønskelig å stige eller opprettholde høyde, og deaktivere når du går ned eller lander. Alt dette skjer ved atmosfæretrykk, antatt konstant i en viss høyde ikke langt fra overflaten..
Damp genereres i kjeler ved å varme opp vann og holde trykket konstant. Etterpå utfører denne dampen en brukbar jobb, for eksempel å generere elektrisitet i termoelektriske anlegg eller aktivere andre mekanismer som lokomotiver og vannpumper..
Det er 40 liter gass ved en temperatur på 27 ºC. Finn volumøkningen når varme tilsettes isobarisk til den når 100 ºC.
Charles lov brukes til å bestemme det endelige volumet, men Merk følgende: temperaturene må uttrykkes i kelvin, bare legge til 273 K til hver:
27 ºC = 27 + 273 K = 300 K
100 ºC = 100 + 273 K = 373 K
Fra:
V1/ T1 = Vto/ Tto ⇒ Vto = Tto(V1/ T1) = 373 ºC (40 L / 300 K) = 49,7 L
Endelig er volumøkningen Vto - V1 = 49,7 l - 40 l = 9,7 l.
Leveres 5,00 x 103 J av energi til en ideell gass for å utføre 2,00 x 103 J jobber med miljøet sitt i en isobarisk prosess. Det blir bedt om å finne:
a) Endringen i gassens indre energi.
b) Volumendringen, hvis nå den indre energien reduseres med 4,50 x 103 J og 7,50 x 10 blir kastet ut3 J i systemet, med tanke på konstant trykk på 1,01 x 105 Pa.
Brukt ∆U = Q - W og verdiene gitt i uttalelsen er erstattet: Q = 5,00 x 103 J og W = 2,00 x 103 J:
=5,00 x 103 J - 2,00 x 103 J = 3,00 x 103 J
Derfor øker gassens indre energi med 3,00 x 103 J.
Volumendringen finnes i det utførte arbeidet: W = P∆V:
∆U = Q - W = Q - P∆V
Uttalelsen sier at den indre energien avtar, derfor: ∆U= -4,50 x 103 J. Det forteller oss også at en viss mengde varme drives ut: Q = -7,50 x 103 J. I begge tilfeller representerer det negative tegnet reduksjon og tap, så:
-4,50 x 103 J = -7,50 x 103 J - P∆V
Hvor P = 1,01 x 105 Pa. Siden alle enhetene er i det internasjonale systemet, fortsetter vi med å løse volumendringen:
∆V = (-4,50 x 103 J +7,50 x 103 J) / (- 1,01 x 105 Pa) = -2,97 x 10-to m3
Siden volumendringen er negativ, betyr det at volumet gikk ned, det vil si at systemet ble kontrakt.
Ingen har kommentert denne artikkelen ennå.