
Hva er spenningsdeleren? (med eksempler)
De spenningsdeler eller spenningsdeler består av en forening av motstander eller impedanser i serie koblet til en kilde. På denne måten spenningen V levert av kilden - inngangsspenning - fordeles proporsjonalt i hvert element, i henhold til Ohms lov:
VJeg = I.ZJeg.
Hvor VJeg er spenningen over kretselementet, jeg er strømmen som strømmer gjennom den og ZJeg den tilsvarende impedansen.
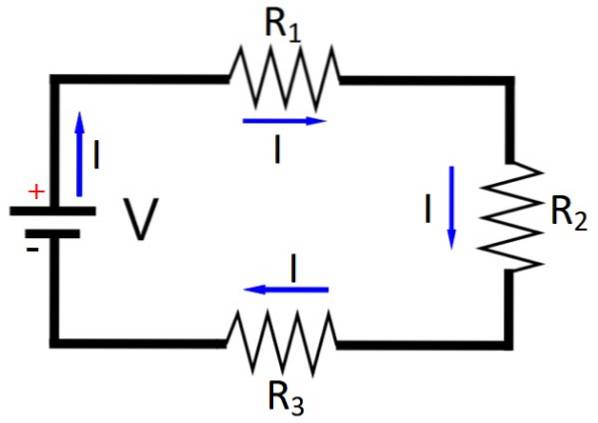
Når du ordner kilden og elementene i en lukket krets, må Kirchhoffs andre lov oppfylles, som sier at summen av all spenningen faller og stiger er lik 0.
For eksempel, hvis kretsen som skal vurderes er rent motstandsdyktig og en 12 volt kilde er tilgjengelig, bare ved å plassere to identiske motstander i serie med kilden, vil spenningen bli delt: hver motstand vil ha 6 volt. Og med tre identiske motstander oppnås 4 V i hver enkelt.
Siden kilden representerer en spenningsstigning, så er V = +12 V. Og i hver motstand er det spenningsfall som er representert med negative tegn: - henholdsvis - 6 V og - 6 V. Det er lett å se at Kirchoffs andre lov er oppfylt:
+12 V - 6 V - 6 V = 0 V
Det er her navnet på spenningsdeleren kommer fra, fordi det gjennom seriemotstander lett kan oppnås lavere spenninger fra en kilde med høyere spenning.
Artikkelindeks
- 1 Spenningsdelerligningen
- 1.1 Spenningsdeler med 2 motstander
- 2 Arbeidseksempler
- 2.1 - Eksempel 1
- 2.2 - Eksempel 2
- 3 Referanser
Spenningsdelerligningen
La oss fortsette å vurdere en ren resistiv krets. Vi vet at strømmen I som går gjennom en motstandskrets i serie koblet til en kilde som vist i figur 1, er den samme. Og ifølge Ohms lov og Kirchoffs andre lov:
V = IR1 + Å GÅto + Å GÅ3 +… Å GÅJeg
Hvor R1, Rto... RJeg representerer hver seriemotstand i kretsen. Derfor:
V = I ∑ RJeg
Så strømmen viser seg å være:
I = V / ∑ RJeg
La oss nå beregne spenningen over en av motstandene, motstanden RJeg for eksempel:
VJeg = (V / ∑ RJeg) RJeg
Den forrige ligningen blir omskrevet som følger, og vi har spenningsdelerregelen klar for et batteri og N-motstand i serie:
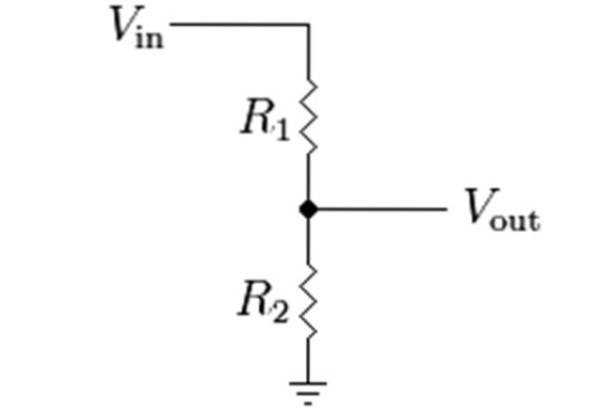
Spenningsdeler med 2 motstander
Hvis vi har en spenningsdelerkrets med to motstander, blir ligningen ovenfor:

Og i spesielle tilfeller der R1 = Rto, VJeg = V / 2, uansett strøm, som angitt i begynnelsen. Dette er den enkleste spenningsdeleren av alle.
I den følgende figuren er diagrammet til denne skillelinjen, hvor V, inngangsspenningen, er symbolisert som Vi, og VJeg er spenningen som oppnås ved å dele spenningen mellom motstandene R1 og Rto.

Arbeidet eksempler
Spenningsdelerregelen vil bli brukt i to resistive kretser for å oppnå lavere spenninger.
- Eksempel 1
En 12 V-kilde er tilgjengelig, som må deles inn i 7 V og 5 V ved hjelp av to motstander R1 og Rto. Det er en 100 Ω fast motstand og en variabel motstand hvis område er mellom 0 og 1 kΩ. Hvilke alternativer er det for å konfigurere kretsen og sette verdien på motstanden Rto?
Løsning
For å løse denne øvelsen vil spenningsdeleren for to motstander bli brukt:

Anta at R1 er motstanden funnet ved en spenning på 7 V og der er den faste motstanden R plassert1 = 100 Ω
Den ukjente motstanden Rto må være på 5 V:

Og R1 ved 7 V:

5 (Rto +100) = 12 Rto
500 = 7 Rto
Rto = 71,43 Ω
På samme måte kan du bruke den andre ligningen for å oppnå samme verdi, eller erstatte resultatet oppnådd for å sjekke om det er likeverd.
Hvis nå den faste motstanden er plassert som Rto, da blir det R1 er på 7 V:


5 (100 + R.1) = 100 x 12
500 + 5R1 = 1200
R1 = 140 Ω
På samme måte er det mulig å verifisere at denne verdien tilfredsstiller den andre ligningen. Begge verdiene er i det variable motstandsområdet, derfor er det mulig å implementere den forespurte kretsen på begge måter.
- Eksempel 2
Et likestrøm voltmeter for å måle spenninger i et bestemt område, er basert på spenningsdeleren. For å bygge et slikt voltmeter kreves et galvanometer, for eksempel D'Arsonval.
Det er en måler som oppdager elektriske strømmer, utstyrt med en gradert skala og en indikasjonsnål. Det er mange modeller av galvanometre, den i figuren er en veldig enkel, med to tilkoblingsterminaler som er på baksiden..

Galvanometeret har en indre motstand RG, som bare tåler en liten strøm, kalt maksimal strøm IG. Følgelig er spenningen over galvanometeret V.m = JegGRG.
For å måle spenning plasseres voltmeteret parallelt med elementet som skal måles, og dets indre motstand må være stor nok til ikke å trekke strøm fra kretsen, ellers vil den endre den..
Hvis vi vil bruke galvanometeret som en måler, må spenningen som måles ikke overstige det maksimalt tillatte, som er den maksimale nedbøyningen av nålen som enheten har. Men vi antar at Vm er liten, siden jegG og RG de er.
Imidlertid når galvanometeret er koblet i serie med en annen motstand RS, anrop begrensende motstand, vi kan utvide måleområdet til galvanometeret fra den lille Vm opp til en viss høyere spenning ε. Når denne spenningen er nådd, opplever instrumentnålen maksimal nedbøyning.
Designskjemaet er som følger:
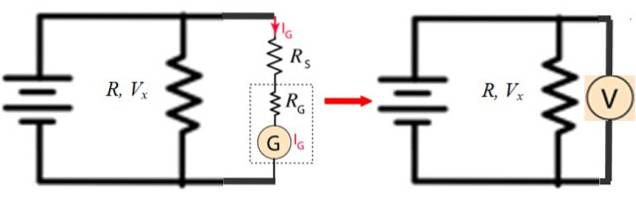
I figur 4 til venstre er G galvanometeret og R er hvilken motstand du vil måle spenningen V.x.
Figuren til høyre viser hvordan kretsen med G, RG og RS tilsvarer et voltmeter, som er plassert parallelt med motstanden R.
1V fullskala voltmeter
Anta for eksempel at den indre motstanden til galvanometeret er RG = 50 Ω og maksimal strøm den støtter er IG = 1 mA beregnes begrensningsmotstanden RS for voltmeteret som er bygget med dette galvanometeret for å måle en maksimal spenning på 1 V som følger:
JegG (RS + RG) = 1 V.
RS = (1 V / 1 x 10-3 A) - RG
RS = 1000 Ω - 50 Ω = 950 Ω
Referanser
- Alexander, C. 2006. Grunnleggende om elektriske kretser. 3.. Utgave. Mc Graw Hill.
- Boylestad, R. 2011. Introduksjon til kretsanalyse. 2. plass. Utgave. Pearson.
- Dorf, R. 2006. Introduksjon til elektriske kretser. 7. Utgave. John Wiley & Sons.
- Edminister, J. 1996. Elektriske kretser. Schaum-serien. 3.. Utgave. Mc Graw Hill
- Figueroa, D. Physics Series for Sciences and Engineering. Vol.5 Elektrostatikk. Redigert av D. Figueroa. USB.
- Hyperfysikk. Design av voltmeter. Gjenopprettet fra: hyperphysics.phy-astr.gsu.edu.
- Wikipedia. Spenningsdeler. Gjenopprettet fra: es.wikipedia.org.


Ingen har kommentert denne artikkelen ennå.