
Hva er det magnetiske øyeblikket?
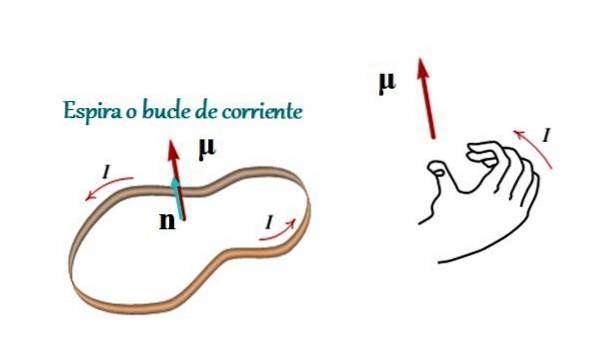
De magnetisk øyeblikk er en vektor som relaterer strømmen som passerer gjennom en sløyfe eller lukket sløyfe med sitt område. Modulen er lik produktet av strømmen og områdets intensitet, og retning og følelse er gitt av høyre regel, som vist i figur 1.
Denne definisjonen er gyldig uavhengig av formen på sløyfen. Når det gjelder enheten til magnetmomentet, er det Ampere × m i det internasjonale systemet for SI-enheterto.
I matematiske termer, betegner den magnetiske momentvektoren med den greske bokstaven μ (i fet skrift fordi det er en vektor og dermed skiller seg fra størrelsen), uttrykkes det som:
μ = AI n
Hvor jeg er intensiteten til strømmen, er A området som er omsluttet av sløyfen og n er enhetsvektoren (med en modul lik 1) som peker i retningen vinkelrett på sløyfens plan, og hvis sans er gitt av regelen om høyre tommel (se figur 1).
Denne regelen er veldig enkel: ved å krølle de fire fingrene på høyre hånd for å følge strømmen, indikerer tommelen retning og følelse av retning. n og derfor det magnetiske øyeblikket.
Ovennevnte ligning er gyldig for en sløyfe. Hvis det er N-svinger som i en spole, multipliseres magnetmomentet med N:
μ = NAI n
Artikkelindeks
- 1 Magnetisk moment og magnetfelt
- 1.1 Dipolens magnetfelt
- 2 Effekt av et eksternt felt på løkken
- 2.1 Dreiemoment på en rektangulær sløyfe
- 2.2 Potensiell energi til den magnetiske dipolen
- 3 Referanser
Magnetisk øyeblikk og magnetfelt
Det er lett å finne uttrykk for det magnetiske øyeblikk av svinger med vanlige geometriske former:
-Firkantet sidesving ℓ: μ = Iℓto n
-Rektangulær sidespiral til Y b: μ = Iab n
-Sirkulær spiral med radius R: μ = IπRto n
Dipole magnetfelt
Magnetfeltet produsert av løkken eller strømsløyfen ligner veldig på en stavmagnet og også jordens.
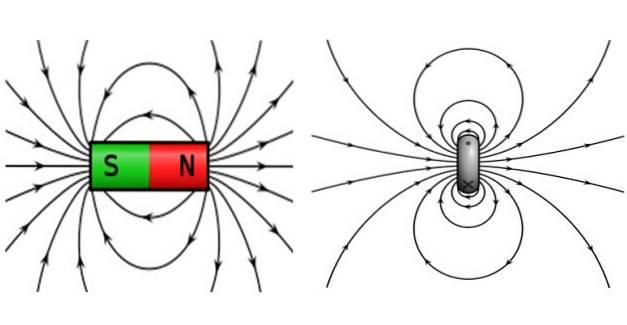
Stangmagneter er preget av å ha en nordpol og en sydpol, hvor motsatte poler tiltrekker seg og som poler frastøter. Feltlinjene er stengt, de forlater nordpolen og kommer til sørpolen.
Nå er magnetpolene uatskillelige, noe som betyr at hvis du deler en stavmagnet i to mindre magneter, har de fortsatt sine egne nord- og sørpoler. Det er ikke mulig å ha isolerte magnetpoler, det er derfor stangmagneten kalles magnetisk dipol.
Magnetfeltet til en sirkulær sløyfe med radius R, som bærer en strøm I, beregnes ved hjelp av Biot-Savart-loven. For punktene som tilhører symmetriaksen (i dette tilfellet x-aksen), er feltet gitt av:

Forholdet mellom magnetfeltet og dipolens magnetiske øyeblikk
Inkludert det magnetiske øyeblikket i forrige uttrykk resultater:

På denne måten er intensiteten til magnetfeltet proporsjonal med magnetmomentet. Merk at feltintensiteten synker med kuben av avstanden.
Denne tilnærmingen gjelder for alle sløyfer, så lenge x er stor i forhold til dimensjonene.
Og siden linjene i dette feltet er så like linjemagnetens, er ligningen en god modell for dette magnetfeltet og for andre systemer hvis linjer er like, for eksempel:
-Ladede partikler i bevegelse som elektronet.
-Atomet.
-Jorden og andre planeter og satellitter i solsystemet.
-Stjerner.
Effekt av et eksternt felt på løkken
En veldig viktig egenskap ved magnetmomentet er dens kobling til dreiemomentet som sløyfen opplever i nærvær av et eksternt magnetfelt..
En elektrisk motor inneholder spoler som en strøm i skiftende retning går gjennom, og som takket være det ytre feltet opplever en spinnende effekt. Denne rotasjonen får en akse til å bevege seg og den elektriske energien blir omgjort til mekanisk energi under prosessen..
Dreiemoment på en rektangulær løkke
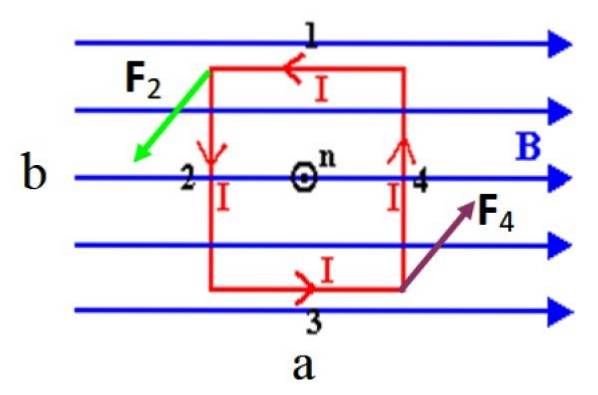
Anta, for å gjøre det lettere å beregne, en rektangulær sløyfe med sider til Y b, hvis normale vektor n, projiserer til skjermen, i utgangspunktet vinkelrett på et jevnt magnetfelt B, som i figur 3. Sidene av løkken opplever krefter gitt av:
F = JegL x B
Hvor L er en størrelsesvektor lik segmentets lengde og rettet i henhold til strømmen, er jeg dens intensitet og B er feltet. Kraften er vinkelrett på begge deler L når det gjelder feltet, men ikke alle sider opplever kraft.

I figuren vist er det ingen kraft på kortsidene 1 og 3 fordi de er parallelle med feltet, husk at kryssproduktet mellom parallelle vektorer er null. Imidlertid er langsidene 2 og 4 som er vinkelrette på B, oppleve kreftene betegnet som Fto Y F4.
Disse kreftene dannes et par: de har samme størrelse og retning, men motsatte retninger, derfor er de ikke i stand til å overføre sløyfen midt i feltet. Men de kan rotere det, siden dreiemomentet τ utøvd av hver kraft, i forhold til den vertikale aksen som går gjennom sentrum av sløyfen, har samme retning og sans.
I henhold til definisjonen av dreiemoment, hvor r er posisjonsvektoren:
τ = r x F
Deretter:
τto = τ4=(a / 2) F (+j )
De enkelte momentene avbrytes ikke, siden de har samme retning og sans, så de blir lagt til:
τnett = τto + τ4 = a F (+j )
Og å være størrelsen på kraften F = IbB, resulterer det:
τnett = I⋅a⋅b⋅B (+j )
Produktet a⋅b er området A på sløyfen, så Iab er størrelsen på det magnetiske øyeblikket μ. Derfor τnett = μ⋅B (+j )
Det kan sees at dreiemomentet generelt sammenfaller med vektorproduktet mellom vektorene μ Y B:
τnett = μ x B
Og selv om dette uttrykket ble avledet fra en rektangulær sløyfe, er det gyldig for en flat sløyfe med vilkårlig form.
Effekten av feltet på løkken er et dreiemoment som har en tendens til å justere magnetmomentet med feltet.
Potensiell energi til den magnetiske dipolen
For å rotere sløyfen eller dipolen midt i feltet, må det jobbes mot den magnetiske kraften, som endrer dipolens potensielle energi. Variasjonen av energien ΔU når svingen roterer fra vinkelen θeller vinkelen θ er gitt av integralen:

ΔU = -μB cos θ
Som igjen kan uttrykkes som prikkproduktet mellom vektorene B Y μ:
ΔU = - μB
Minimum potensiell energi i dipolen oppstår når cos θ = 1, som betyr at μ Y B de er parallelle, energien er maksimal hvis de er motsatte (θ = π) og det er null når de er vinkelrette (θ = π / 2).
Referanser
- Figueroa, D. 2005. Serie: Physics for Sciences and Engineering. Volum 5. Elektromagnetisme. Redigert av Douglas Figueroa (USB).
- Resnick, R. 1999. Fysikk. Vol. 2. 3. utgave på spansk. Compañía Editorial Continental S.A. av C.V.
- Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 2. Pearson.
- Serway, R., Jewett, J. (2008). Fysikk for naturvitenskap og ingeniørfag. Volum 2. 7.. Ed. Cengage Learning.
- Tipler, P. (2006) Fysikk for vitenskap og teknologi. 5. utg. Bind 2. Redaksjonell Reverté.



Ingen har kommentert denne artikkelen ennå.