
Hva er akustisk impedans? Søknader og øvelser
De akustisk impedans eller spesifikk akustisk impedans er motstanden til materialmediene mot passering av lydbølger. Det er konstant for et bestemt medium, som går fra et steinete lag i det indre av jorden til det biologiske vevet.
Betegner den akustiske impedansen som Z, i matematisk form har vi:
Z = ρ.v
Hvor ρ er tettheten og v lydens hastighet til mediet. Dette uttrykket er gyldig for en plan bølge som beveger seg i en væske.
I SI International System-enheter er tettheten i kg / m3 og hastigheten i m / s. Derfor er enhetene med akustisk impedans kg / mto.s.
På samme måte er den akustiske impedansen definert som kvotienten mellom trykket p og hastigheten:
Z = p / v
Uttrykt på denne måten er Z analog med elektrisk motstand R = V / I, hvor trykk spiller rollen som spenning og hastighet som strømmen. Andre SI-enheter av Z vil være Pa.s / m eller N.s / m3, helt tilsvarende de som er gitt tidligere.
Artikkelindeks
- 1 Overføring og refleksjon av lydbølgen
- 1.1 Overføring og refleksjonskoeffisienter
- 2 Søknader og øvelser
- 2.1 - Øvelse løst 1
- 2.2 - Øvelse løst 2
- 3 Referanser
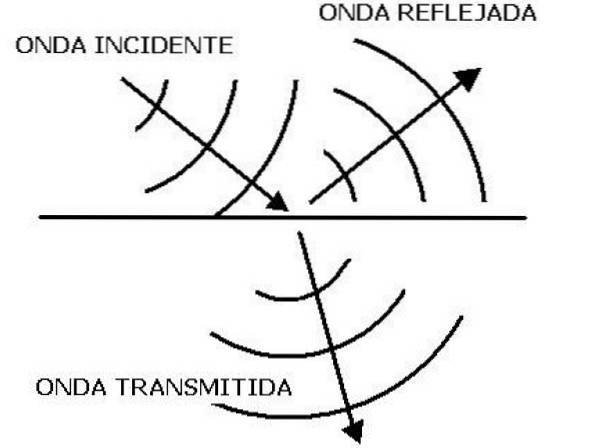
Lydbølgeoverføring og refleksjon
Når du har to midler med forskjellige impedanser Z1 og Zto, en del av en lydbølge som treffer grensesnittet til begge kan overføres og en annen del kan reflekteres. Denne reflekterte bølgen, eller ekkoet, er den som inneholder viktig informasjon om det andre mediet..
Måten energien som transporteres av bølgen fordeles på, avhenger av refleksjonskoeffisientene R og overføringskoeffisienten T, to meget nyttige størrelser for å studere forplantningen av lydbølgen. For refleksjonskoeffisienten er det kvotienten:
R = jegr / JEGeller
Hvor jegeller er intensiteten til hendelsesbølgen og jegr er intensiteten til den reflekterte bølgen. På samme måte har vi overføringskoeffisienten:
T = jegt / JEGeller
Nå kan det vises at intensiteten til en plan bølge er proporsjonal med amplituden A:
I = (1/2) Z.ωto .TILto
Der Z er den akustiske impedansen til mediet og ω er bølgefrekvensen. På den annen side er kvotienten mellom den overførte amplituden og den innfallende amplituden:
TILt/TILeller = 2Z1/ (Z1 +Zto)
Som tillater kvotienten jegt / JEGeller uttrykkes i form av amplitudene til hendelsen og overførte bølger som:
Jegt / JEGeller = ZtoTILtto / Z1TILellerto
Ved hjelp av disse uttrykkene oppnås R og T i form av den akustiske impedansen Z.
Overføring og refleksjonskoeffisienter
Ovennevnte kvotient er nøyaktig overføringskoeffisienten:
T = (Zto/ Z1) [2.Z1/ (Z1 +Zto)]to = 4Z1Zto / (Z1 +Zto)to
Siden det ikke er tenkt på tap, er det sant at hendelsesintensiteten er summen av den overførte intensiteten og den reflekterte intensiteten:
Jegeller = Jegr + Jegt → (Ir / JEGeller) + (Jegt / JEGeller) = 1
Dette lar oss finne et uttrykk for refleksjonskoeffisienten når det gjelder impedansene til de to mediene:
R + T = 1 → R = 1 - T
Gjennomføring av en liten algebra for å omorganisere vilkårene, er refleksjonskoeffisienten:
R = 1 - 4Z1Zto / (Z1 +Zto)to = (Z1 - Zto)to/ (Z1 +Zto)to
Og da informasjonen relatert til det andre mediet er funnet i den reflekterte pulsen, er refleksjonskoeffisienten av stor interesse..
Dermed, når de to mediene har stor forskjell i impedans, blir telleren til det forrige uttrykket større. Da er intensiteten til den reflekterte bølgen høy og inneholder god informasjon om mediet..
Når det gjelder den delen av bølgen som overføres til det andre mediet, falmer den gradvis og energien forsvinner som varme..
Søknader og øvelser
Overførings- og refleksjonsfenomener gir opphav til flere svært viktige bruksområder, for eksempel ekkolodd utviklet under andre verdenskrig og brukt til å oppdage gjenstander. Forresten, noen pattedyr som flaggermus og delfiner har et innebygd ekkoloddsystem.
Disse egenskapene er også mye brukt til å studere det indre av jorden i seismiske letemetoder, i ultralydmedisinsk bildebehandling, bentetthetsmåling og avbildning av forskjellige strukturer for feil og mangler..
Akustisk impedans er også en viktig parameter når man vurderer lydresponsen til et musikkinstrument..
- Løst øvelse 1
Ultralydsteknikken for å avbilde biologisk vev bruker høyfrekvente lydpulser. Ekkoene inneholder informasjon om organer og vev de passerer gjennom, som en programvare er ansvarlig for å oversette til et bilde.
En ultralydspuls rettet mot fett-muskelgrensesnittet er snittet. Med de oppgitte dataene, finn:
a) Den akustiske impedansen til hvert vev.
b) Prosentandelen av ultralyd reflektert i grensesnittet mellom fett og muskler.
Fett
- Tetthet: 952 kg / m3
- Lydhastighet: 1450 m / s
Muskel
- Tetthet: 1075 kg / m3
- Lydhastighet: 1590 m / s
Løsning til
Den akustiske impedansen til hvert vev er funnet ved å erstatte i formelen:
Z = ρ.v
På denne måten:
Zfett = 952 kg / m3 x 1450 m / s = 1,38 x 106 kg / mto.s
Zmuskel = 1075 kg / m3 x 1590 m / s = 1,71 x 106 kg / mto.s
Løsning b
For å finne prosentandelen av intensiteten som reflekteres i grensesnittet til de to vevene, brukes refleksjonskoeffisienten gitt av:
R = (Z1 - Zto)to/ (Z1 +Zto)to
Her Zfett = Z1 og Zmuskel = Zto. Refleksjonskoeffisienten er en positiv størrelse, som er garantert av kvadratene i ligningen.
Bytte ut og evaluere:
R = (1,38 x 106 - 1,71 x 106 )to / (1,38 x 106 + 1,71 x 106 )to = 0,0114.
Når vi multipliserer med 100, vil prosentandelen reflekteres: 1,14% av hendelsesintensiteten.
- Trening løst 2
En lydbølge har et intensitetsnivå på 100 desibel og faller normalt på vannoverflaten. Bestem intensitetsnivået til den overførte bølgen og den reflekterte bølgen.
Data:
Vann
- Tetthet: 1000 kg / m3
- Lydhastighet: 1430 m / s
Luft
- Tetthet: 1,3 kg / m3
- Lydhastighet: 330 m / s
Løsning
Intensitetsnivået i desibel av en lydbølge, betegnes som L, er dimensjonsløst og er gitt av formelen:
L = 10 logg (I / 10-12)
Heving til 10 på begge sider:
10 L / 10 = I / 10-12
Siden L = 100, resulterer det i:
Jeg / 10-12 = 1010
Enheter for intensitet er gitt i form av effekt per arealenhet. I det internasjonale systemet er de Watt / mto. Derfor er intensiteten til hendelsesbølgen:
Jegeller = 1010 . 10-12 = 0,01 W / mto.
For å finne intensiteten til den overførte bølgen, beregnes overføringskoeffisienten, og deretter multipliseres med hendelsesintensiteten.
De respektive impedansene er:
ZVann = 1000 kg / m3 x 1430 m / s = 1,43 x 106 kg / mto.s
Zluft = 1,3 kg / m3 x 330 m / s = 429 kg / mto.s
Å erstatte og evaluere i:
T = 4Z1Zto / (Z1 +Zto)to = 4 × 1,43 x 106 x 429 / (1,43 x 106 + 429)to = 1,12 x 10-3
Så intensiteten til den overførte bølgen er:
Jegt = 1,12 x 10-3 x 0,01 W / mto = 1,12 x 10-5 W / mto
Dens intensitetsnivå i desibel beregnes av:
Lt = 10 logg (It / 10-12) = 10 logg (1,12 x 10-5 / 10-12) = 70,3 dB
På sin side er refleksjonskoeffisienten:
R = 1 - T = 0,99888
Med dette er intensiteten til den reflekterte bølgen:
Jegr = 0,99888 x 0,01 W / mto = 9,99 x 10-3 W / mto
Og intensitetsnivået er:
Lt = 10 logg (Ir / 10-12) = 10 logg (9,99 x 10-3 / 10-12) = 100 dB
Referanser
- Andriessen, M. 2003. HSC Physics Course. Jacaranda.
- Baranek, L. 1969. Akustikk. Andre utgave. Redaksjonell Hispano Americana.
- Kinsler, L. 2000. Fundamentals of Acoustics. Wiley og sønner.
- Lowrie, W. 2007. Fundamentals of Geophysics. 2. plass. Utgave. Cambridge University Press.
- Wikipedia. Akustisk impedans. Gjenopprettet fra: en.wikipedia.org.


Ingen har kommentert denne artikkelen ennå.