De geoid Figuren på jorden er den teoretiske overflaten på planeten vår, bestemt av det gjennomsnittlige nivået av havene og med en ganske uregelmessig form. Matematisk er det definert som den ekvipotensielle overflaten til jordens effektive gravitasjonspotensiale, på havnivå.
Siden det er en imaginær (ikke-materiell) overflate, krysser den kontinenter og fjell, som om alle havene var forbundet med vannkanaler som passerer gjennom landmasser..
Jorden er ikke en perfekt sfære, siden rotasjonen rundt aksen gjør den til en slags ball flatet av polene, med daler og fjell. Det er grunnen til at sfæroidformen fremdeles er unøyaktig.
Den samme rotasjonen legger til en sentrifugalkraft til jordens tyngdekraft, hvis resulterende eller effektive kraft ikke peker mot jordens sentrum, men har et visst gravitasjonspotensial knyttet til seg..
I tillegg til dette skaper de geografiske ulykkene uregelmessigheter i tetthet, og derfor opphører tyngdekraften i noen områder definitivt å være sentral..
Så forskere, som begynte med C. F. Gauss, som utviklet den opprinnelige geoiden i 1828, opprettet en geometrisk og matematisk modell for å representere jordoverflaten mer nøyaktig..
For dette antas et hav i ro, uten tidevann eller havstrømmer og med konstant tetthet, hvis høyde fungerer som referanse. Jordens overflate blir da ansett for å bølges forsiktig, stiger der lokal tyngdekraft er størst og synker når den avtar.
La den effektive tyngdeakselerasjonen alltid være vinkelrett på overflaten hvis punkter har samme potensial og resultatet er geoiden, som er uregelmessig siden ekvipotensialet ikke er symmetrisk.
Artikkelindeks
For å bestemme formen på geoiden, som har blitt raffinert over tid, har forskere utført mange målinger, med tanke på to faktorer:
- Den første er at verdien av g, jordens gravitasjonsfelt som tilsvarer tyngdekraftens akselerasjon, avhenger av breddegrad: maksimum ved polene og minimum ved ekvator.
- Det andre er at, som vi sa tidligere, er tettheten på jorden ikke homogen. Det er steder det øker fordi bergartene er tettere, det er en akkumulering av magma eller det er mye bakken på overflaten, for eksempel et fjell.
Der tettheten er høyere, g det er det også. Noter det g er en vektor, og det er derfor den er angitt med fet skrift.
For å definere geoiden, er potensialet på grunn av tyngdekraften nødvendig, som gravitasjonsfeltet må defineres som tyngdekraften per masseenhet.
Hvis en testmasse m er plassert i nevnte felt, er kraften som utøves av jorden på dens vekt P = mg, derfor er feltets størrelse:
Kraft / masse = P / m = g
Vi vet allerede middelverdien: 9,8 m / sto og hvis jorden var sfærisk, ville den være rettet mot sentrum. I henhold til Newtons lov om universell gravitasjon:
P = Gm M / rto
Der M er jordens masse og G er den universelle gravitasjonskonstanten. Så størrelsen på gravitasjonsfeltet g Det er:
g = GM / rto
Det ser mye ut som et elektrostatisk felt, så det kan defineres et gravitasjonspotensial som er analogt med elektrostatisk:
V = -GM / r
Konstanten G er den universelle konstanten for gravitasjon. Vel, overflatene som gravitasjonspotensialet alltid har den samme verdien kalles ekvipotensielle overflater Y g det er alltid vinkelrett på dem, som sagt før.
For denne spesielle klassen av potensial er de ekvipotensielle overflatene konsentriske kuler. Arbeidet som kreves for å flytte en masse på dem er null, fordi kraften alltid er vinkelrett på hvilken som helst bane på ekvipotensialet.
Siden jorden ikke er sfærisk, må tyngdeakselerasjonen ha en lateral komponent gl på grunn av sentrifugalakselerasjon forårsaket av rotasjonsbevegelsen til planeten rundt sin akse.
Følgende figur viser denne komponenten i grønt, hvis størrelse er:
gl = ωtotil
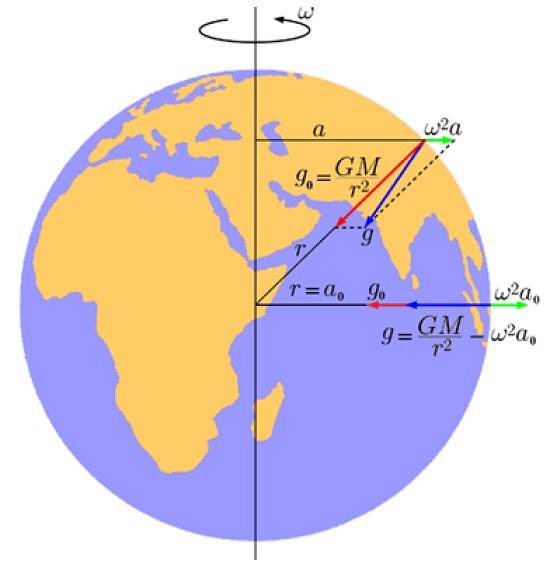
I denne ligningen ω er jordens rotasjonshastighet til er avstanden mellom punktet på jorden, på en viss breddegrad og aksen.
Og i rødt er komponenten som skyldes planetarisk gravitasjonsattraksjon:
geller = GM / rto
Som et resultat, ved å legge til vektor geller + gl, en resulterende akselerasjon oppstår g (i blått) som er den sanne akselerasjonen av jordens tyngdekraft (eller effektiv akselerasjon), og at den som vi ser ikke peker nøyaktig mot sentrum.
Videre avhenger sidekomponenten av breddegrad: den er null ved polene, og tyngdefeltet er derfor maksimalt der. Ved ekvator motsetter den seg gravitasjonsattraksjonen, og reduserer den effektive tyngdekraften, hvis størrelse forblir:
g = GM / rto - ωtoR
Med R = jordens ekvatoriale radius.
Det er nå forstått at de ekvipotensielle overflatene på jorden ikke er sfæriske, men har en slik form at g alltid være vinkelrett på dem på alle punkter.
Her er den andre faktoren som påvirker variasjonen av jordens gravitasjonsfelt: de lokale variasjonene av tyngdekraften. Det er steder hvor tyngdekraften øker fordi det er mer masse, for eksempel på bakken i figur a).
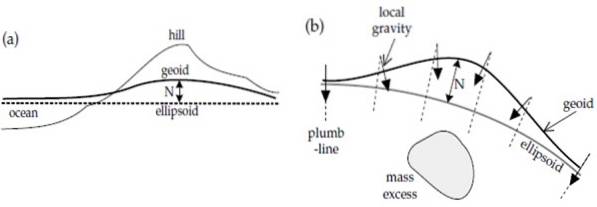
Eller det er en opphopning eller overskudd av masse under overflaten, som i b). I begge tilfeller er det en høyde i geoiden fordi jo større masse, jo større intensitet av gravitasjonsfeltet..
På den annen side, over havet, er tettheten lavere, og som en konsekvens synker geoiden, som vi ser til venstre på figur a), over havet..
Fra figur b) kan det også sees at lokal tyngdekraft, indikert med piler, alltid er vinkelrett på overflaten av geoiden, som vi har sagt. Dette skjer ikke alltid med referansen ellipsoid.
Figuren indikerer også, med en toveis pil, høydeforskjellen mellom geoid og ellipsoid, som kalles kupert y betegnes som N. Positive bølger er relatert til overflødig masse og negative bølger til mangler.
Bølgene overstiger nesten aldri 200 m. Verdiene avhenger faktisk av hvordan havnivået som fungerer som referanse velges, siden noen land velger forskjellig i henhold til deres regionale egenskaper..
-På geoiden er det effektive potensialet, resultatet av potensialet på grunn av tyngdekraften og sentrifugalpotensialet, konstant.
-Tyngdekraften virker alltid vinkelrett på geoiden, og horisonten er alltid tangensiell for den.
-Geoiden tilbyr en referanse for kartleggingsapplikasjoner med høy presisjon.
-Ved hjelp av geoiden kan seismologer oppdage dybden der jordskjelv oppstår.
-GPS-posisjonering avhenger av hvilken geoid som skal brukes som referanse.
-Havoverflaten er også parallell med geoiden.
-Geoidens høyder og nedstigninger indikerer overdreven eller massefeil, som er gravimetriske anomalier. Når en avvik oppdages, og avhengig av verdien, er det mulig å utlede den geologiske strukturen til undergrunnen, i det minste til visse dybder..
Dette er grunnlaget for gravimetriske metoder innen geofysikk. En gravimetrisk anomali kan indikere opphopning av visse mineraler, strukturer begravet under jorden, eller til og med tomme rom. Saltkuplene i undergrunnen, som kan påvises ved gravimetriske metoder, er i noen tilfeller indikative for tilstedeværelse av olje.
Ingen har kommentert denne artikkelen ennå.