
Simpsons regelformel, bevis, eksempler, øvelser
De simpsons regjerer er en metode for å beregne, på en tilnærmet måte, bestemte integraler. Den er basert på å dele integrasjonsintervallet i et jevnt antall jevnt fordelte underintervaller.
De ekstreme verdiene av to påfølgende delintervaller definerer tre punkter, hvor en parabel, hvis ligning er et andregrads polynom, passer til.
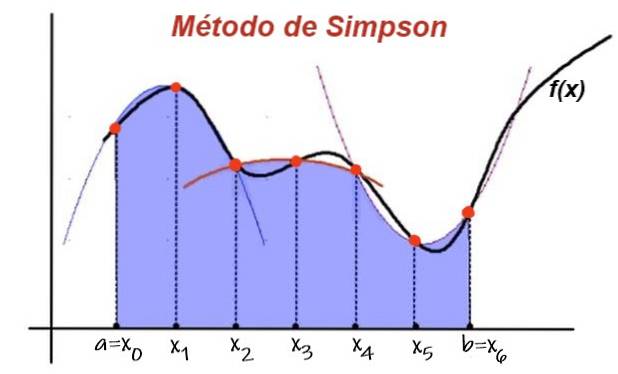
Deretter tilnærmes området under kurven til funksjonen i de to påfølgende intervallene av området til interpolasjonspolynomet. Når vi legger til bidraget til området under parabolen av alle de påfølgende delintervallene, har vi den omtrentlige verdien av integralen.
På den annen side, siden integralen til en parabel kan beregnes algebraisk nøyaktig, er det mulig å finne en analytisk formel for den omtrentlige verdien til den bestemte integralen. Det er kjent som Simpsons formel.
Feilen i det omtrentlige oppnådde resultatet reduseres ettersom antall underavdelinger n er større (der n er et partall).
Et uttrykk vil bli gitt nedenfor som tillater estimering av den øvre grensen for feilen i tilnærmingen til integralet I, når en partisjon av n regelmessige delintervaller av det totale intervallet er laget [a, b].
Artikkelindeks
- 1 Formel
- 2 Demo
- 2.1 Koeffisienter for interpolasjonspolynomet
- 2.2 Beregning av den omtrentlige integralen i [Xi, Xi + 2]
- 2.3 Omtrentlig beregning av integralen i [a, b]
- 2.4 Feil på tilnærming
- 3 Arbeidede eksempler
- 3.1 - Eksempel 1
- 3.2 - Eksempel 2
- 3.3 - Eksempel 3
- 4 Foreslått øvelse
- 5 Referanser
Formel
Integreringsintervallet [a, b] er delt inn i n delintervaller hvor n er et jevnt heltall. Bredden på hver underavdeling vil være:
h = (b - a) / n
På denne måten blir partisjonen laget i intervallet [a, b]:
X0, X1, X2,…, Xn-1, Xn
Hvor X0 = a, X1 = X0 + h, X2 = X0 + 2h,…, Xn-1 = X0 + (n-1) h, Xn = X0 + nh = b.
Formelen som gjør det mulig å beregne den bestemte integralen I i den kontinuerlige, og helst glatte, funksjonen på intervallet [a, b] på en omtrentlig måte er:
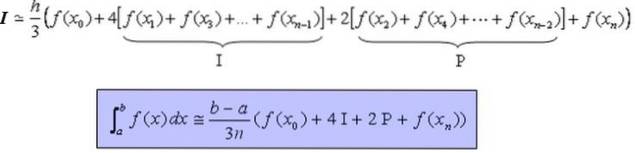
Demonstrasjon
For å oppnå Simpsons formel tilnærmes funksjonen f (X) i hvert delintervall [Xi, Xi + 2] med et andregrads polynom p (X) (parabel) som passerer gjennom de tre punktene: [Xi, f (Xi)] ; [Xi + 1, f (Xi + 1)] og [Xi + 2, f (Xi + 2)].
Deretter beregner vi integralet av polynomet p (x) i [Xi, Xi + 2] som tilnærmer seg integralet av funksjonen f (X) i det intervallet.
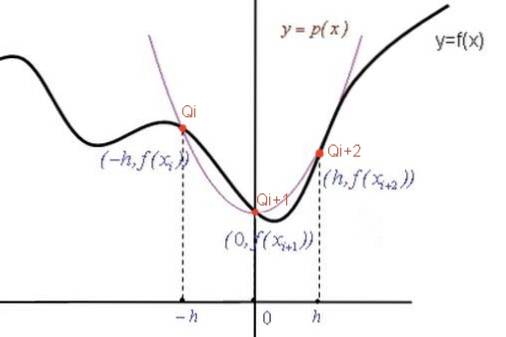
Koeffisienter for interpolasjonspolynomet
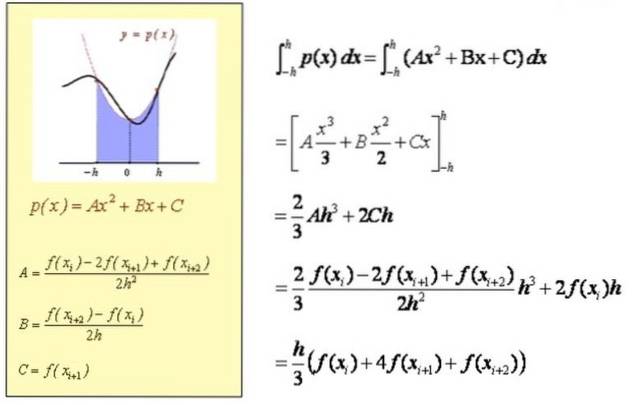
Ligningen til parabolen p (X) har den generelle formen: p (X) = A Xto + B X + C. Når parabolen passerer gjennom punktene Q angitt med rødt (se figur), blir koeffisientene A, B, C bestemt fra følgende ligningssystem:
A (-h)to - B h + C = f (Xi)
C = f (Xi + 1)
A (h)to + B h + C = f (Xi + 2)
Det kan sees at koeffisienten C bestemmes. For å bestemme koeffisienten A legger vi til den første og tredje ligningen som oppnår:
2 A hto + 2 C = f (Xi) + f (Xi + 2).
Deretter erstattes verdien av C og A fjernes, og etterlater:
A = [f (Xi) - 2 f (Xi + 1) + f (Xi + 2)] / (2 hto)
For å bestemme koeffisienten B trekkes den tredje ligningen fra den første og B løses, og oppnår:
B = [f (Xi + 2) - f (Xi)] = 2 timer.
Oppsummert har andregrads polynom p (X) som passerer gjennom punktene Qi, Qi + 1 og Qi + 2 koeffisienter:
A = [f (Xi) - 2 f (Xi + 1) + f (Xi + 2)] / (2 hto)
B = [f (Xi + 2) - f (Xi)] = 2 timer
C = f (Xi + 1)
Beregning av den omtrentlige integralen i [Xi, Xi + 2]
Omtrentlig beregning av integralen i [a, b]
Som allerede nevnt, blir det på det totale integrasjonsintervallet [a, b] laget en partisjon X0, X1, X2,…, Xn-1, Xn med trinn h = Xi + 1 - Xi = (b - a) / n , hvor n er et partall.
Omtrentlig feil
Merk at feilen avtar med den fjerde effekten av antall underinndelinger i intervallet. For eksempel, hvis du går fra n underavdelinger til 2n, reduseres feilen med en faktor 1/16.
Den øvre grensen for feilen oppnådd gjennom Simpson-tilnærmingen kan fås fra samme formel, og erstatter det fjerde derivatet med den maksimale absolutte verdien til det fjerde derivatet i intervallet [a, b].
Arbeidet eksempler
- Eksempel 1
Tenk på funksjonen funksjonen f (X) = 1 / (1 + Xto).
Finn den bestemte integralen av funksjonen f (X) i intervallet [-1, 1] ved å bruke Simpsons metode med to underavdelinger (n = 2).
Løsning
Vi tar n = 2. Grensene for integrasjon er a = -1 og b = -2, så partisjonen ser slik ut:
X0 = -1; X1 = 0 og X2 = +1.
Derfor har Simpsons formel følgende form:

Med n = 2 → xo = -1, x1 = 0; x2 = 1, derfor:

- Eksempel 2
Tenk på funksjonen f (X) = 1 / (1 + Xto).
Finn den bestemte integralen av funksjonen f (X) i intervallet [-1, 1] ved å bruke Simpsons formel med fire underavdelinger (n = 4).
Løsning
Vi tar n = 4. Grensene for integrasjon er a = -1 og b = -2, så partisjonen ser slik ut:
X0 = -1; X1 = -1/2; X2 = 0; X3 = 1/2 og X4 = +1.
Simpsons formel er uttalt slik:
Integrert ≃ [(b -a) / (3 n)] [f (X0) + 4 I + 2 P + f (Xn)]
For saken der den blir brukt, er det som følger:
Integrert ≃ (1 - (1)) / (3⋅4)] [f (-1) + 4 [f (-½) + f (½)] + 2 [f (0)] + f (1)
Integrert ≃ (2/12) [½ + 4 (⅘ + ⅘) + 2⋅1 + ½] = (⅙) [47/5] = 47/30 = 1,5666
- Eksempel 3
Bestem den bestemte integralen av de foregående eksemplene nøyaktig, og foreta en sammenligning av det eksakte resultatet med de som er oppnådd ved bruk av Simpsons formel i eksemplene 1a og 1b..
Løsning
Den ubestemte integralen av funksjonen f (X) = 1 / (1 + Xto) er funksjonen arctan (X).
Når man evaluerer i grensen for integrasjon, forblir det:
Integrert = arctan (1) - arctan (-1) = π / 4 - (-π / 4) = π / 2 = 1,5708
Hvis vi sammenligner resultatet av den eksakte løsningen med den som ble oppnådd ved Simpsons metode med n = 2 og n = 4, har vi:
For n = 2 er forskjellen mellom den nøyaktige og den omtrentlige løsningen π / 2 - 5/3 = -0,0959, det vil si en prosentvis forskjell på -0,06%.
Og for Simpson-tilnærmingen med n = 4, er forskjellen mellom den nøyaktige og den omtrentlige løsningen π / 2 - 47/30 = 0,0041, det vil si en prosentvis forskjell på 0,003%.
Foreslått øvelse
Simpsons metode er egnet til å brukes i programmeringsspråk og i dataprogrammer for matematiske beregninger. Det foreslås at leseren, basert på formlene gitt i denne artikkelen, skriver sin egen kode i favorittprogrammet.
Følgende figur viser en øvelse der Simpsons formel er implementert i Smath studio, gratis programvare tilgjengelig for operativsystemer Windows Y Android.

Referanser
- Casteleiro, J. M. 2002. Integral calculus (Illustrated edition). Madrid: ESIC-redaksjon.
- UPV. Simpsons metode. Polytechnic University of Valencia. Gjenopprettet fra: youtube.com
- Purcell, E. 2007. Calculus Ninth Edition. Prentice hall.
- Wikipedia. Simpsons regel. Gjenopprettet fra: es.wikipedia.com
- Wikipedia. Lagrange polynomisk interpolasjon. Gjenopprettet fra: es.wikipedia.com



Ingen har kommentert denne artikkelen ennå.