
Proportionalitetsforholdskonsept, eksempler og øvelser
De proporsjonalitetsforhold de er koblinger mellom to eller flere variabler, slik at når en av mengdene varierer, gjør verdien av de andre også. For eksempel, hvis en øker, kan de andre øke eller redusere, men i en jevn mengde..
Gamle greske matematikere innså at noen variabler var relatert på en veldig presis måte. De innså at hvis en sirkel er dobbelt så stor som en annen, vil den ha en omkrets dobbelt så lang.

Og hvis diameteren blir tredoblet, vil omkretsens kontur også tredobles. Dette betyr at en økning i diameter gir en proporsjonal økning i størrelsen på omkretsen..
Og slik kan vi bekrefte at lengden på omkretsen L er proporsjonal med diameteren D, som uttrykkes som følger:
L ∝ D
Hvor symbolet ∝ lyder "direkte proporsjonal med”. For å endre proporsjonalitetssymbolet til det for likhet og innlemme numeriske verdier, er det nødvendig å bestemme koblingen mellom variablene, kalt konstant av proporsjonalitet.
Etter å ha tatt mange målinger bestemte de gamle matematikerne at proporsjonalitetskonstanten mellom størrelsen L på omkretsen, og diameteren på den samme, var tallet 3.1416 ... Ellipsene indikerer et uendelig antall desimaler.
Denne verdien er ingen ringere enn det berømte tallet π (pi), og på denne måten skriver vi:
L = π.D
På denne måten er forholdet mellom lengde og diameter på en omkrets det samme som forholdet mellom lengden og diameteren til en annen. Og det beste er at nå har vi en måte å beregne lengden på en hvilken som helst omkrets bare ved å kjenne dens diameter.
Artikkelindeks
- 1 Eksempler på proporsjonalitetsforhold
- 2 Direkte proporsjonalitet og omvendt proporsjonalitet
- 3 Andre typer proporsjonalitet
- 4 Øvelser
- 4.1 - Øvelse 1
- 4.2 - Øvelse 2
- 5 Referanser
Eksempler på forholdsmessige forhold
I vitenskapen (og også i hverdagen) er det veldig viktig å finne sammenhenger mellom variabler, å vite hvordan endringer i den ene påvirker den andre. For eksempel:
-Hvis du trenger 3 kopper mel for å lage et dusin informasjonskapsler. Hvor mange kopper tar det å lage to og et halvt dusin?.
-Å vite at en gjenstand på planeten Merkur veier 4 ganger mindre enn på jorden, hvor mye vil en bil på 1,5 tonn veie på kvikksølv??
-Hvordan påvirker endringen i den påførte kraften akselerasjonen i kroppen den påføres??
-Hvis et kjøretøy kjører med jevn rettlinjet bevegelse på en motorvei, og vi vet at det kjører 30 km på 10 minutter, hva blir avstanden etter 20 minutter?
-Når vi har en ledning som en elektrisk strøm går gjennom, hvordan varierer spenningen mellom endene hvis den øker?
-Hvis diameteren til en sirkel er doblet, hvordan påvirkes dens område??
-Hvordan påvirker avstand intensiteten til det elektriske feltet som produseres av en punktladning?
Svaret ligger i forholdsmessige forhold, men ikke alle forhold er av samme type. Så finner vi dem for alle situasjonene som er reist her.
Direkte proporsjonalitet og omvendt proporsjonalitet
To variabler x og y er i direkte proporsjon hvis de er relatert av:
y = kx
Hvor k er konstanten av proporsjonaliteten. Et eksempel er forholdet mellom mengdene mel og kaker. Hvis vi tegner graf for disse variablene, får vi en rett linje som den som er vist i figuren:
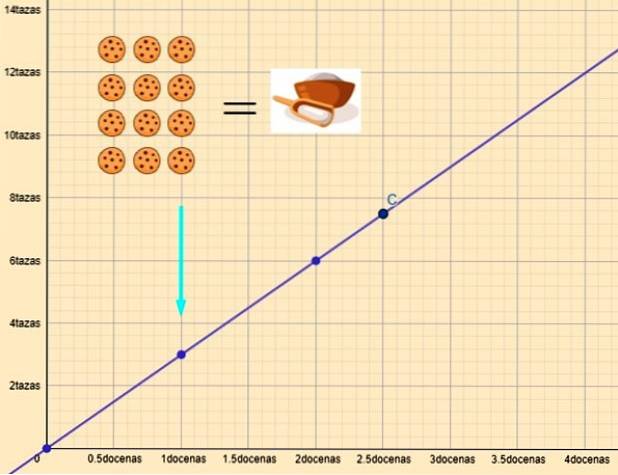
Hvis y er koppene med mel og x er dusin informasjonskapslene, er forholdet mellom dem:
y = 3x
For x = 1 dusin trenger vi y = 3 kopper mel. Og for x = 2,5 dusin kreves y = 7,5 kopp mel.
Men vi har også:
-Akselerasjon til at en kropp opplever er proporsjonal med kraften F handler på det, blir kroppens masse, kalt m, proporsjonalitetskonstanten:
F = mtil
Derfor, jo større kraft som påføres, jo større blir akselerasjonen..
-I ohmske ledere er spenningen V mellom endene proporsjonal med strømmen jeg påførte. Proportionalitetskonstanten er lederens motstand R:
V = RI
-Når et objekt beveger seg med jevn rettlinjet bevegelse, avstanden d er proporsjonal med tiden t, være hastigheten v proporsjonalitetskonstanten:
d = v.t
Noen ganger finner vi to størrelser slik at en økning i ett gir en avta proporsjonal i den andre. Denne avhengigheten kalles omvendt forhold.
For eksempel, i den forrige ligningen, er tiden t som kreves for å kjøre en viss avstand d omvendt proporsjonal med hastigheten v på reisen:
t = d / v
Og så mens høyere er hastigheten v, mindre tiden det tar bilen å kjøre avstanden d. Hvis for eksempel doblingen blir doblet, kuttes tiden i to.
Når to variabler x og y er i omvendt proporsjon, kan vi skrive:
y = k / x
Å være k konstanten av proporsjonalitet. Grafen for denne avhengigheten er:
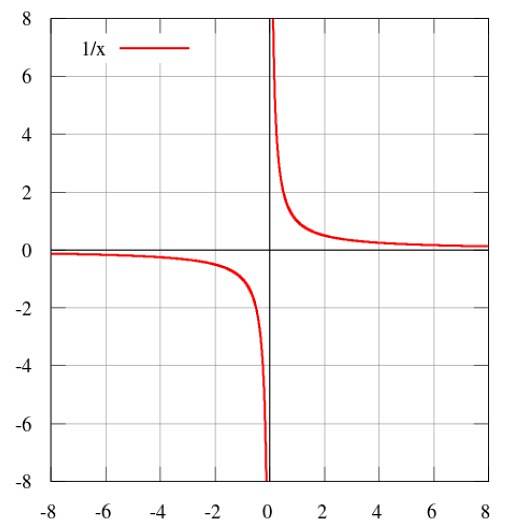
Andre typer proporsjonalitet
I et av eksemplene nevnt tidligere lurte vi på hva som skjer med sirkelområdet når radiusen øker. Svaret er at området er direkte proporsjonalt med kvadratet til radiusen, der π er proporsjonalitetskonstanten:
A = πRto
Hvis radius blir doblet, vil området øke med en faktor 4.
Og når det gjelder det elektriske feltet OG produsert av en poengladning hva, det er kjent at intensiteten synker med det inverse av kvadratet til avstanden r til lasten hva:
E = kog q / rto
Men vi kan også si at feltets intensitet er direkte proporsjonal med størrelsen på ladningen, og er proporsjonalitetskonstanten kog, den elektrostatiske konstanten.
Andre proporsjonaliteter som også presenteres i Science er eksponentiell proporsjonalitet og logaritmisk proporsjonalitet. I det første tilfellet er variablene x og y relatert av:
y = k.ax
Der a er basen, et annet positivt tall enn 0, som vanligvis er 10 eller tallet e. For eksempel har den eksponentielle veksten av bakterier denne formen.
I det andre tilfellet er forholdet mellom variablene:
y = k.logtil x
Igjen er a basen til logaritmen, som ofte er 10 (desimal logaritme) eller e (naturlig logaritme).
Opplæring
- Øvelse 1
Å vite at et objekt veier fire ganger mindre på planeten Merkur enn på jorden, hvor mye vil en bil på 1,5 tonn veie på kvikksølv??
Løsning
Vekt på kvikksølv = (1/4) Vekt på jorden = (1/4) x 1,5 tonn = 0,375 tonn.
- Øvelse 2
For en fest bestemmer noen venner seg for å tilberede juice fra fruktkonsentrat. Instruksjonene på pakken sier at ett glass konsentrat lager 15 glass juice. Hvor mye kraftfôr som trengs for å lage 110 glass juice?
Løsning
La oss være antall glass juice og x antall konsentrat. De er beslektet av:
y = kx
Ved å erstatte verdiene y = 15 og x = 1, løses konstanten k:
k = y / x = 15/1 = 15
Derfor:
110 = 15 x
x = 110/15 = 7,33 glass fruktkonsentrat.
Referanser
- Baldor, A. 1974. Algebra. Cultural Venezolana S.A.
- Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. Sjette. Ed prentice hall.
- Varsity Tutors. Forholdsmessige forhold. Gjenopprettet fra: varsitytutors.com
- Wikipedia. Proporsjonalitet Gjenopprettet fra: es.wikipedia.org.
- Zill, D. 1984. Algebra og trigonometri. Mcgraw hill.



Ingen har kommentert denne artikkelen ennå.