Vektoregenskaper og egenskaper, elementer, typer, eksempler

De vektor De er matematiske enheter som har en -positiv-størrelse, vanligvis ledsaget av en måleenhet, samt retning og sans. Slike egenskaper er veldig passende for å beskrive fysiske størrelser som hastighet, kraft, akselerasjon og mange flere..

Med vektorer er det mulig å utføre operasjoner som addisjon, subtraksjon og produkter. Inndeling er ikke definert for vektorer, og som for produktet, det er tre klasser som vi vil beskrive senere: punktprodukt eller punkt, vektorprodukt eller kryss og produkt av en skalar med en vektor.

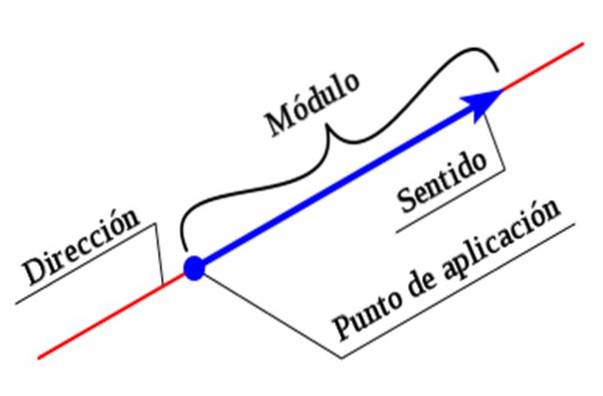
For å fullstendig beskrive en vektor, er det nødvendig å indikere alle dens egenskaper. Størrelsen eller modulen er en numerisk verdi ledsaget av en enhet, mens retning og retning er etablert ved hjelp av et koordinatsystem.

La oss se på et eksempel: La oss si at et fly flyr fra en by til en annen med en hastighet på 850 km / t i N-retning. Her har vi en fullt spesifisert vektor, siden størrelsen er tilgjengelig: 850 km / t, mens retningen og sansen er NE.

Vektorer er vanligvis representert grafisk av orienterte linjesegmenter, hvis lengde er proporsjonal med størrelsen.

Mens det skal spesifiseres retning og følelse, kreves det en referanselinje, som vanligvis er den horisontale aksen, selv om nord også kan tas som referanse, er det tilfellet med flyets hastighet:

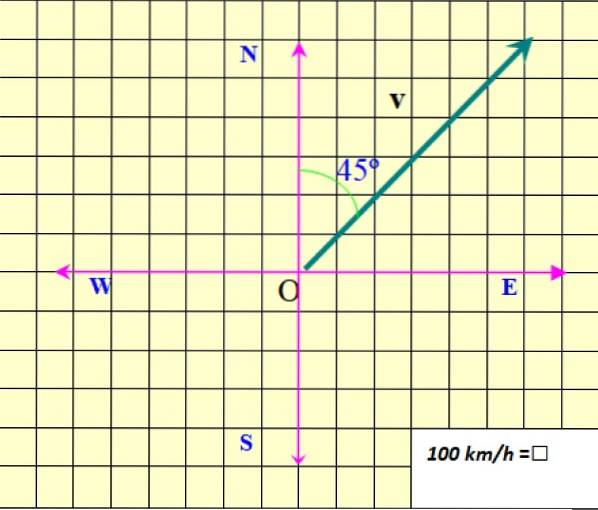
Figuren viser hastighetsvektoren til planet, som er betegnet som v på dristig, for å skille den fra en skalar mengde, som bare krever en numerisk verdi og noen enhet som skal spesifiseres.

Artikkelindeks

• 1 Element av en vektor
  • 1.1 Rektangulære komponenter i en vektor
• 2 typer
  • 2.1 Ortogonale enhetsvektorer
• 3 Summen av vektorer
  • 3.1 Egenskaper ved vektortilsetning
• 4 vektoreksempler
• 5 Andre operasjoner mellom vektorer
  • 5.1 Produkt av skalar og vektor
  • 5.2 Skalarprodukt eller prikkprodukt mellom vektorer
  • 5.3 Kryssprodukt eller kryssprodukt mellom vektorer
• 6 Løst øvelser
  • 6.1 - Øvelse 1
  • 6.2 - Øvelse 2
• 7 Referanser

Elementer av en vektor

Som vi har sagt, er elementene i vektoren:

-Størrelse eller modul, noen ganger også kalt absolutt verdi eller norm for vektoren.

-Retning

-Føle

I eksemplet i figur 2, modulen v Det er 850 km / t. Modulen er betegnet som v uten fet skrift, eller som |v|, hvor stolpene representerer den absolutte verdien.

Adressen til v er spesifisert med hensyn til Nord. I dette tilfellet er det 45 º nord for øst (45 º NØ). Til slutt informerer spissen av pilen om retningen på v.

I dette eksemplet er opprinnelsen til vektoren tegnet sammenfallende med opprinnelsen O til koordinatsystemet, dette er kjent som bundet vektor. På den annen side, hvis opprinnelsen til vektoren ikke sammenfaller med referansesystemets, sies det å være en gratis vektor.

Det skal bemerkes at for å spesifisere vektoren fullt ut, må disse tre elementene noteres, ellers ville beskrivelsen av vektoren være ufullstendig.

Rektangulære komponenter i en vektor

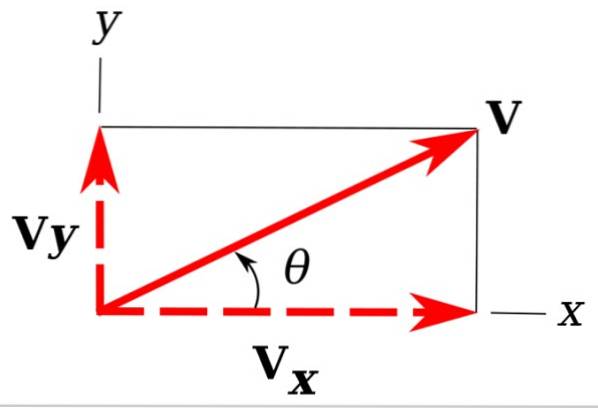
På bildet har vi eksempelvektoren vår tilbake v, det er i flyet xy.

Det er lett å se at projeksjonene av v på x- og y-koordinataksene bestemmer en rett trekant. Disse anslagene er v_Y Y v_x og kalles rektangulære komponenter av v.

En måte å betegne v gjennom sine rektangulære komponenter er slik: v = x, v_Y>. Disse parentesene brukes i stedet for parenteser for å understreke at det er en vektor og ikke et punkt, siden i dette tilfellet parenteser vil bli brukt.

Hvis vektoren er i et tredimensjonalt rom, trengs det en komponent til, slik at:

v = x, v_Y, v_z>

Å kjenne de rektangulære komponentene, beregnes vektors størrelse, tilsvarende det å finne hypotenusen til høyre trekant hvis ben er v_x Y v_Y,. Ved hjelp av Pythagoras teorem følger det at:

|v|^to = (v_x)^to +  (v_Y)^to

Polær form av en vektor

Når størrelsen på vektoren er kjent |v| og vinkelen θ som dette dannes med referanseaksen, vanligvis den horisontale aksen, er vektoren også spesifisert. Vektoren sies da å uttrykkes i polær form.

De rektangulære komponentene beregnes i dette tilfellet enkelt:

v_x = |v| .cos θ

v_Y = |v| .sen θ

I henhold til ovenstående, de rektangulære komponentene i hastighetsvektoren v av flyet ville være:

v_x = 850. cos 45º km / t = 601,04 km / t

v_Y = 850. sin 45º km / t = 601,04 km / t

Typer

Det er flere typer vektorer. Det er vektorer med hastighet, posisjon, forskyvning, kraft, elektrisk felt, momentum og mange flere. Som vi allerede har sagt, i fysikk er det et stort antall vektormengder.

Når det gjelder vektorer som har visse egenskaper, kan vi nevne følgende typer vektorer:

-Null: dette er vektorer med størrelse 0 og som er betegnet som 0. Husk at den fete bokstaven symboliserer de tre grunnleggende egenskapene til en vektor, mens den normale bokstaven kun representerer modulen.

For eksempel, på et legeme i statisk likevekt, må summen av krefter være en nullvektor.

-Gratis og bundet: gratisvektorer er de hvis opprinnelses- og ankomstpunkter er et par punkter i planet eller i rommet, i motsetning til sammenkoblede vektorer, hvis opprinnelse sammenfaller med referansesystemet som brukes til å beskrive dem.

Paret eller øyeblikket produsert av et par krefter er et godt eksempel på en fri vektor, siden paret ikke gjelder noe bestemt punkt.

-Teamlinser: de er to gratisvektorer som har identiske egenskaper. Derfor har de like stor styrke, retning og sans.

-Coplanar eller coplanar: vektorer som tilhører samme plan.

-Motsetninger: vektorer med lik størrelse og retning, men motsatt retning. Vektoren overfor en vektor v er vektoren -v og summen av begge er nullvektoren: v + (-v) = 0.

-Samtidig: vektorer hvis handlingslinjer alle går gjennom samme punkt.

-Glidere: er de vektorene hvis applikasjonspunkt kan gli langs en bestemt linje.

-Kollinær: vektorer som er plassert på samme linje.

-Enhetlig: de vektorene hvis modul er 1.

Ortogonale enhetsvektorer

Det er en veldig nyttig type vektor i fysikk som kalles en ortogonal enhetsvektor. Den ortogonale enhetsvektoren har en modul lik 1 og enhetene kan være hvilke som helst, for eksempel de med hastighet, posisjon, kraft eller andre.

Det er et sett med spesielle vektorer som hjelper deg med å enkelt representere andre vektorer og til å utføre operasjoner på dem: de er ortogonale enhetsvektorer Jeg, j Y k, enhetlig og vinkelrett på hverandre.

I to dimensjoner er disse vektorene rettet langs den positive retningen til begge aksene x fra aksen Y. Og i tre dimensjoner legges en enhetsvektor til i retning av aksen z positivt. De er representert som følger:

Jeg = <1, 0,0>

j = < 0,1,0>

k = <0,0,1>

En vektor kan representeres av enhetsvektorene Jeg, j Y k som følger:

v = v_x Jeg + v_Y j + v_z k

For eksempel hastighetsvektoren v fra eksemplene ovenfor kan skrives som:

v = 601,04 Jeg + 601.04 j km / t

Komponenten i k er ikke nødvendig, siden denne vektoren er i flyet.

Vector tillegg

Summen av vektorer vises veldig ofte i forskjellige situasjoner, for eksempel når du vil finne den resulterende kraften på et objekt som er påvirket av forskjellige krefter. Tenk å begynne med at vi har to gratisvektorer eller Y v på flyet, som vist i følgende figur til venstre:

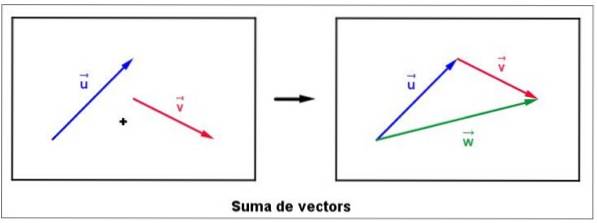
Den flyttes umiddelbart forsiktig til vektoren v, uten å endre størrelsen, retningen eller sansen, slik at dens opprinnelse sammenfaller med slutten av eller.

Sumvektoren kalles w og tegnes fra u slutter på v, i henhold til riktig figur. Det er viktig å merke seg at størrelsen på vektoren w er ikke nødvendigvis summen av størrelsen på v Y eller.

Hvis du tenker nøye på det, er den eneste gangen at størrelsen på den resulterende vektoren er summen av størrelsen på tilleggene, når begge tilleggene er i samme retning og har samme sans..

Og hva skjer hvis vektorene ikke er gratis? Det er også veldig enkelt å legge dem til. Måten å gjøre det på er å legge komponent til komponent eller analytisk metode.

Som et eksempel, la oss se på vektorene i følgende figur, det første er å uttrykke dem på en av de kartesiske måtene som tidligere er forklart:

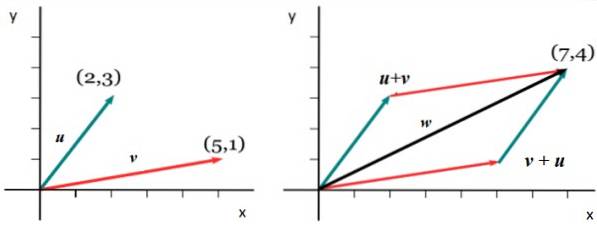
v = <5,1>

eller = <2,3>

For å få komponenten inn x av sumvektoren w, de respektive komponentene er lagt til x fra v Y eller: w_x = 5 + 2 = 7. Og å få w_Y en analog prosedyre følges: w_Y = 1 + 3. Derfor:

eller = <7,4>

Egenskaper ved vektortilsetning

-Summen av to eller flere vektorer resulterer i en annen vektor.

-Det er kommutativt, rekkefølgen på tilleggene endrer ikke summen på en slik måte at:

eller + v = v + eller

-Det nøytrale elementet i summen av vektorer er nullvektoren: v + 0 = v

-Subtraksjonen av to vektorer er definert som summen av det motsatte: v - u = v + (-eller)

Vektoreksempler

Som vi har sagt, er det mange vektormengder i fysikk. Blant de mest kjente er:

-Posisjon

-Forskyvning

-Gjennomsnittlig hastighet og øyeblikkelig hastighet

-Akselerasjon

-Makt

-Mengden bevegelse

-Moment eller moment av en kraft

-Impuls

-elektrisk felt

-Magnetfelt

-Magnetisk øyeblikk

På den annen side er de ikke vektorer, men skalarer:

-Vær

-Masse

-Temperatur

-Volum

-Tetthet

-Mekanisk arbeid

-Energi

-Varmt

-Makt

-Spenning

-Elektrisk strøm

Andre operasjoner mellom vektorer

I tillegg til addisjonen og subtraksjonen av vektorer, er det tre andre veldig viktige operasjoner mellom vektorene, fordi de gir opphav til nye veldig viktige fysiske størrelser:

-Produkt av en skalar og en vektor.

-Punktproduktet eller punktproduktet mellom vektorene

-Og kors- eller vektorproduktet mellom to vektorer.

Produkt av en skalar og en vektor

Tenk på Newtons andre lov, som sier at styrken F og akselerasjon til de er proporsjonale. Konstanten av proporsjonalitet er massen m av objektet, derfor:

F = m.til

Masse er en skalar; kraft og akselerasjon er vektorer. Siden kraften oppnås ved å multiplisere massen med akselerasjonen, er det resultatet av produktet av en skalar og en vektor.

Denne typen produkter resulterer alltid i en vektor. Her er et annet eksempel: mengden bevegelse. Være P momentumvektoren, v hastighetsvektoren og som alltid, m er massen:

P = m.v

Punktprodukt eller prikkprodukt mellom vektorene

Vi har plassert mekanisk arbeid på listen over mengder som ikke er vektorer. Arbeid i fysikk er imidlertid resultatet av en operasjon mellom vektorer som kalles skalarprodukt, indre produkt eller prikkprodukt..

La vektorene være v Y eller, prikkproduktet eller skalaren mellom dem er definert som:

v∙eller = |v| ∙ |eller | .cos θ

Hvor θ er vinkelen mellom de to. Fra ligningen som vises følger det umiddelbart at resultatet av punktproduktet er en skalar, og at hvis begge vektorene er vinkelrette, er deres skalarprodukt 0.

Tilbake til mekanisk arbeid W, dette er det skalære produktet mellom kraftvektoren F og forskyvningsvektoren ℓ.

W = F∙ℓ                  

Når vektorer er tilgjengelige når det gjelder komponentene, er punktproduktet også veldig enkelt å beregne. Ja v = x, v_Y, v_z > Y eller = x, eller_Y, eller_z >, prikkproduktet mellom de to er:

v∙eller = v_x eller_x + v_Y eller_Y + v_z eller_z

Punktproduktet mellom vektorene er kommutativ, derfor:

v∙eller = eller∙v

Kryss produkt eller vektorprodukt mellom vektorer

Ja v og u er våre to eksempelvektorer, vektorproduktet er definert som:

v x eller = w

Det følger umiddelbart at kryssproduktet resulterer i en vektor, hvis modul er definert som:

|v x u | = | v | . | u |. sen θ

Hvor θ er vinkelen mellom vektorene.

Kryssproduktet er derfor ikke kommutativt v x u ≠ u x v. Faktisk v x u = - (u x v).

Hvis de to eksempelvektorene uttrykkes som enhetsvektorene, er beregningen av vektorproduktet lettere:

v = v_x Jeg + v_Y j + v_z k

eller = u_x Jeg + eller_Y j + eller_z k

Kryss produkter mellom enhetsvektorer

Tverrproduktet mellom identiske enhetsvektorer er null, siden vinkelen mellom dem er 0º. Men mellom forskjellige enhetsvektorer er vinkelen mellom dem 90º og sin 90º = 1.

Følgende diagram hjelper deg med å finne disse produktene. I retning av pilen har den en positiv retning og i motsatt retning har den en negativ retning:

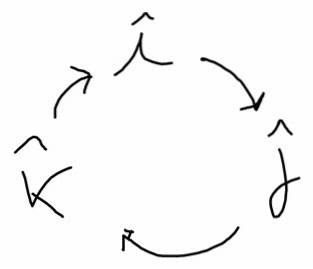
Jeg x j = k, j x k = Jeg; k x Jeg = j; j x i = -k; k x j = -Jeg; Jeg x k = -j

Ved å bruke distribusjonsegenskapen, som fremdeles er gyldig for produktene mellom vektorer pluss egenskapene til enhetsvektorer, har vi:

v x eller = (v_x Jeg + v_Y j + v_z k) x (u_x Jeg + eller_Y j + eller_z k) =  

= (v_Yeller_z - v_zeller_Y )Jeg + (v_zeller_x - v_xeller_z )j + (v_xeller_Y - v_Yeller_x )k

Løst øvelser

- Øvelse 1

Gitt vektorene:

v = -5 Jeg + 4j + 1 k

eller = 2 Jeg -3 j + 7k

Hva skal være vektoren w slik at summen v + eller + w det viser seg 6 Jeg +8 j -10k?

Løsning

-5 Jeg + 4j + 1 k

to Jeg -3 j + 7k

 w_x Jeg + w_Y j + w_z k  +

--

6Jeg + 8 j -10 k

Derfor må det oppfylles at:

-5 +2 + w_x = 6 → w_x = 9

4-3 + w_Y = 8 → w_Y = 7

1 + 7 + w_z = -10 → w_z = -18

Svaret er: w = 9 Jeg +7 j - 18k

- Øvelse 2

Hva er vinkelen mellom vektorene v Y eller fra øvelse 1?

Løsning

Vi vil bruke prikkproduktet. Fra definisjonen har vi:

cos θ = v∙eller / |v| ∙ |eller|

v∙eller= -10 -12 + 7 = -15

|v| = √ (-5)^to +4^to +1^to= √42 = 6,48

|eller| = √2^to +(-3)^to +7^to= √62 = 7,87

Erstatter disse verdiene:

cos θ = -15 / 6,48 x 7,87 = -0,2941 → θ = 107,1 º

Referanser

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB).
2. Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. Sjette. Ed prentice hall.
3. Rex, A. 2011. Fundamentals of Physics. Pearson.
4. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 1.
5. Serway, R., Jewett, J. 2008. Physics for Science and Engineering. Volum 1. 7. Ed. Cengage Learning.