De matematisk forhold er koblingen som eksisterer mellom elementene i en delmengde med hensyn til produktet av to sett. EN funksjon involverer den matematiske operasjonen for å bestemme verdien av en avhengig variabel basert på verdien av en uavhengig variabel. Hver funksjon er en relasjon, men ikke alle relasjoner er en funksjon.
| Forhold | Funksjon | |
|---|---|---|
| Definisjon | Delmengde bestilte par som tilsvarer det kartesiske produktet av to sett. | Matematisk operasjon som skal utføres med variabelen x for å få variabelen Y. |
| Notasjon | x R Y; x det er relatert til Y. | Y= ƒ (x); Y er en funksjon av x. |
| Kjennetegn |
|
|
| Eksempler |
|
|
Det kalles den binære relasjonen til et sett A i et sett B eller forholdet mellom elementene i A og B til hvert delmengde C av det kartesiske produktet A x B.
Det vil si at hvis sett A består av elementene 1, 2 og 3, og sett B består av elementene 4 og 5, vil det kartesiske produktet av A x B være de bestilte parene:
A x B = (1,4), (2,4), (3, 4), (1,5), (2,5), (3,5).
Delsettet C = (2,4), (3,5) vil være et forhold mellom A og B siden det består av de ordnede parene (2,4) og (3, 5), resultatet av den kartesiske produkt av A x B.
"La A og B være to ikke-tomme sett, la A x B være produktsettet til begge, det vil si: A x B er dannet av de ordnede parene (x, y) slik at x er elementet i A og Y det er for B. Hvis en delmengde C er definert i A x B, blir en binær relasjon i A og B automatisk bestemt som følger:
x R Y hvis og bare hvis (x, y) ∈ C
(notasjonen x R Y Midler "x det er relatert til Y").
Vi vil kalle sett A startsett og vi vil kalle sett B ankomst sett.
De forholdsdomen er elementene som utgjør startsettet, mens forholdsområde er elementene i ankomstsettet.
Sett TIL fra x elementer av menn i en befolkning og B er settet med Y elementer av kvinner fra samme befolkning. Et forhold opprettes når "x er gift med Y".
Når vi snakker om en matematisk funksjon av et sett A i et sett B, refererer vi til en regel eller mekanisme som relaterer elementene til sett A med et element i sett B.
"Sean x Y Y to virkelige variabler, blir det da sagt at y er en funksjon av x ja til hver verdi jeg tar x tilsvarer en verdi på Y."
Den uavhengige variabelen er x samtidig som Y er den avhengige variabelen eller funksjonen:
y = ƒ (x)
Settet der x det kalles domenet til funksjonen (original) og variasjonen av Y funksjonsområde (bilde).
Sett med par (x, Y) slik at Y= ƒ (x) er kalt funksjonsgraf; hvis de er representert i kartesiske akser, oppnås en familie av poeng kalt funksjonsgraf.
I matematikk får vi mange eksempler på funksjoner. Her er eksempler på flaggskipfunksjoner.
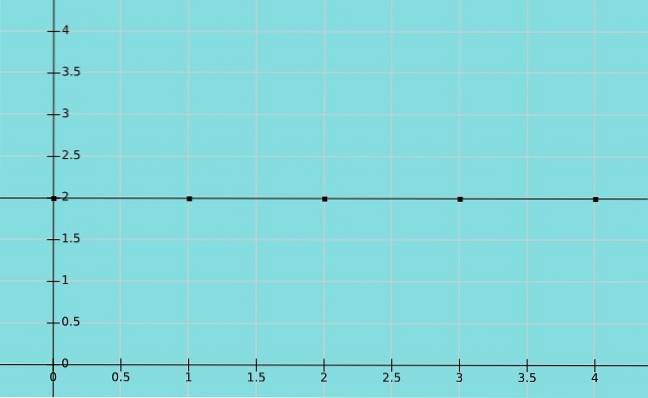
En funksjon kalles konstant hvis elementet i sett B som tilsvarer sett A er det samme. I dette tilfellet tilsvarer alle verdiene til x den samme verdien av y. Dermed er domenet de reelle tallene mens området er en konstant verdi.
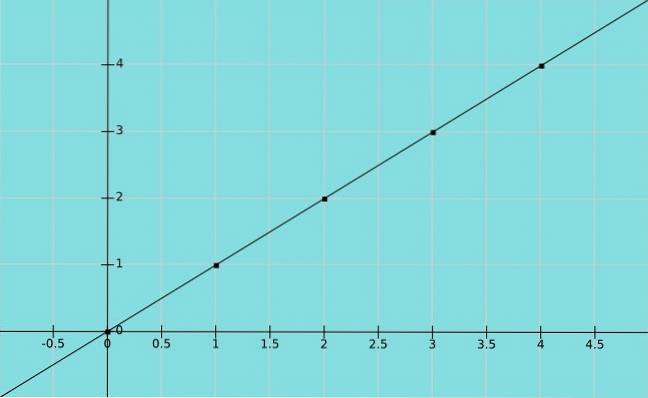
La oss anta x er en variabel og det Y tar samme verdi som x. Vi har da en identitetsfunksjon y = x, hvor parenex, y) i grafen er (1,1), (2,2), (3,3) og så videre.
En polynomfunksjon oppfyller formen y = anxn+tiln-1+xn-1+… + Atoxto+til1x + a0. Grafen over viser funksjonen ƒ (x) = xto+x-2.
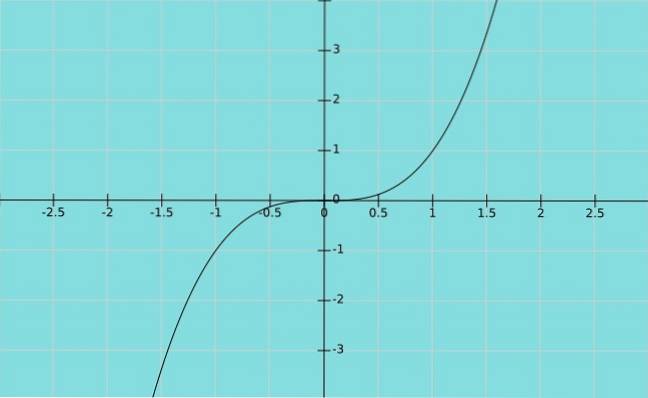
Anta nå at den avhengige variabelen Y er lik den uavhengige variabelen x hevet til terningen. Vi har funksjonen y = x3, hvis graf er vist nedenfor:
Ingen har kommentert denne artikkelen ennå.