
Subtraksjon av vektorer grafisk metode, eksempler, øvelser
De vektor subtraksjon eller vektor subtraksjon mellom vektorer eller Y v betegnet med eller - v, beregnes ved å legge til vektoren eller med vektoren motsatt v. Algebraisk uttrykkes subtraksjonen som følger:
eller - v = eller + (-v)
Det er mulig å utføre vektorsubtraksjon ved å følge forskjellige prosedyrer, for eksempel grafisk, på denne måten en vektor v tegnes av et orientert linjesegment - en pil-.
Lengden på pilen tilsvarer modulen til vektoren, hellingen - i forhold til en gitt referanselinje - indikerer retningen og enden indikerer retningen til vektoren.
Vektoren motsatt v den har samme lengde og retning, men motsatt retning. Så, før du trekker mellom eller Y v, det er nødvendig å tegne vektoren motsatt v, og legg til denne vektoren til u.
Det er veldig viktig å merke seg at vektorsubtraksjon ikke er kommutativ, det vil si at rekkefølgen på vektorene endrer resultatet, derfor:
eller - v ≠ v - eller
Den grafiske prosedyren kan utføres ved hjelp av en av disse metodene, trinnene vi vil forklare nedenfor:
-Trekantmetode.
-Parallelogrammetode.
Artikkelindeks
- 1 Grafisk metode for vektreduksjon
- 1.1 Trekantmetode
- 1.2 Parallelogrammetode
- 2 Eksempler på vektor subtraksjon
- 2.1 - Eksempel 1
- 2.2 - Eksempel 2
- 3 Øvelsen løst
- 3.1 Løsning
- 4 Referanser
Grafisk vektreduksjonsmetode
Trekantmetode
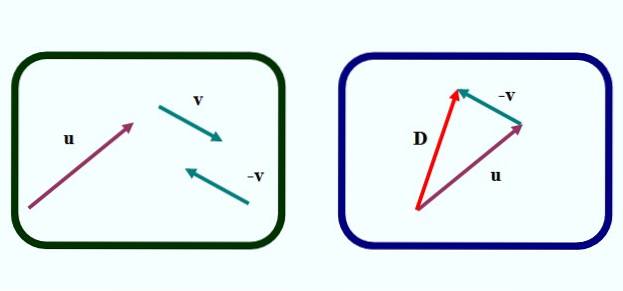
I figur 1 har vi den første av metodene for å trekke to vektorer grafisk. Det handler om trekantmetode, fordi figuren som dannes ved å etablere vektorene er en trekant, som vi kan se på det venstre bildet.
Å gjøre subtraksjonen eller - v vi går frem som følger:
-Tegn vektoren -v fra vektor v, ved oversettelse med linjal og firkant, men endre pilens retning (venstre bilde).
-Flytter til vektor -v på en slik måte at dens opprinnelse sammenfaller med enden av vektoren eller (høyre bilde).
-Deretter tegnes en vektor (i rødt i høyre bilde) som går fra opprinnelsen til eller til slutten av v. Anrop D y er forskjellen vektor:
D = eller - v
Parallelogrammetode
I parallellogrammetoden må vektorene som skal legges til eller trekkes fra sammenfalle på utgangspunktet. Anta at vi vil finne eller - v Med våre vektorer vist ovenfor, er trinnene for å finne subtraksjon av vektorer ved denne metoden som følger:
-Bestem vektoren motsatt v, Hva er det -v, som beskrevet ovenfor for trekantmetoden.
-Oversett nøye vektorer eller Y -v på en slik måte at opprinnelsen deres sammenfaller.
-Nå tegnes segmenterte parallelle linjer fra endene av hver vektor. Figuren som dannes er et parallellogram og i spesielle tilfeller der vektorene er vinkelrette, et resultat av et rektangel eller et kvadrat..
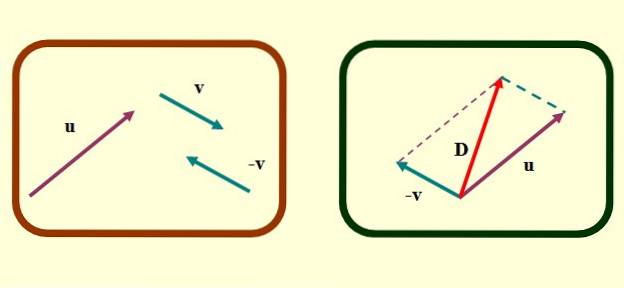
-Til slutt tegnes en vektor som starter fra den felles opprinnelsen til eller Y v til det ytterste der de segmenterte parallelle linjene krysser hverandre. Dette er vektoren D eller subtraksjon.
Viktig
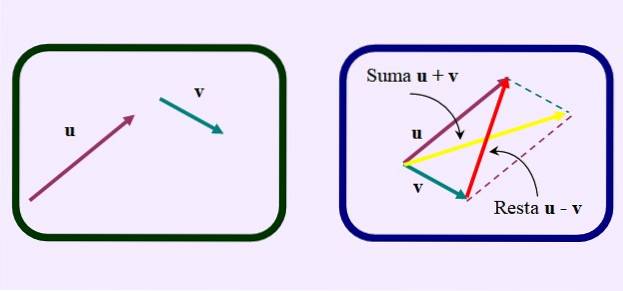
En annen måte å gjøre subtraksjonen på er å tegne parallellogrammet som om du ville legge til vektorene.
Men i stedet for å tegne den vanlige diagonalen til summen, som går fra den felles opprinnelsen til skjæringspunktet mellom parallellene, motsatt eller kortere diagonal, som vist på figuren:
Eksempler på vektor subtraksjon
- Eksempel 1
Et skip seiler på en elv og gjør det i motsatt retning av strømmen. En observatør på land observerer at hastigheten på båten er redusert på grunn av strømens handling.
Hastigheten er en vektor, og i dette eksemplet peker båtens hastighet i en retning, og strømens hastighet har samme retning og motsatt retning. Skipets nettofart er summen av begge vektorene.
For eksempel, hvis båtens instrumenter indikerer at den beveger seg i v '= + 40 km / t og en observatør i fjæra måler at båten beveger seg i v = + 30 km / t. Siden v = v '+ Vc, hvor Vc er strømens hastighet som beregnes ved å trekke henholdsvis hastighetene v og v': Vc = v - v '= 30 km / t - 40 km / t = -10 km / h.
- Eksempel 2
I kinematikk har vi viktige vektorer som beskriver endringer:
-Offset for endringer i posisjon.
-Gjennomsnittlig hastighet, for å kvantifisere hvor raskt posisjonen varierer over tid.
-Akselerasjon, for hastighetsendringer som en funksjon av tiden.
Forskyvningsvektoren
Forskyvningsvektoren beskriver posisjonsendringen som en kropp opplever under bevegelsen.
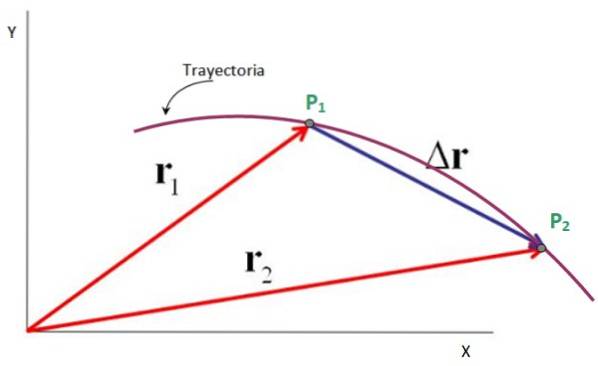
La oss for eksempel se en partikkel som beskriver planbanen vist i figuren, der den passerer fra punkt P1 å peke Pto.
Vektorene rettet fra opprinnelsen til x-y-koordinatsystemet til disse punktene er posisjonsvektorene r1 Y rto, mens forskyvningsvektoren er Δr, som går fra P1 til Pto. Det er sant, det:
Δr = rto - r1
Derfor er forskyvningsvektoren subtraksjonen mellom den endelige posisjonsvektoren og den opprinnelige posisjonsvektoren, som vist i følgende figur. Enhetene har også posisjon: meter, føtter, miles, centimeter og mer..
Gjennomsnittlig hastighet og gjennomsnitt akselerasjonsvektorer
På sin side den gjennomsnittlige hastighetsvektoren vm er definert som forskyvning multiplisert med det inverse av tidsintervallet:


Treningen løst
En partikkel som beskriver en sirkel tar 5 s å passere fra punkt A til punkt B. Ved A har den en hastighet vTIL = 60 km / t mot + x-aksen og ved B er vB = 60 km / t mot + y. Bestem den gjennomsnittlige akselerasjonen grafisk og analytisk.
Løsning
I grafisk form bestemmes retning og retning av gjennomsnittlig akselerasjon av:

I det følgende bildet er subtraksjonen vB - vTIL, ved hjelp av trekantsmetoden, siden den gjennomsnittlige akselerasjonen tilm er proporsjonal med Δv. Den dannede trekanten har de to benene like, og derfor måler de akutte indre vinklene 45 ° hver..

Analytisk, hvis + x-retningen sammenfaller med enhetsvektoren Jeg og + y-retningen med enhetsvektoren j, deretter:
Δv = 60 km / t j - 60 km / t Jeg
Å ta Δt = 5 s, ifølge informasjonen i uttalelsen, er den gjennomsnittlige akselerasjonen:
tilm = (60 km / t j - 60 km / t Jeg) / 5 s = 12 (j-Jeg) km / (h.s)
Referanser
- Bauer, W. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysikk. 2. plass. Ed. McGraw Hill.
- Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 1.
- Tipler, P. 2006. Fysikk for vitenskap og teknologi. 5. utg. Bind 1. Redaksjonell Reverté.



Ingen har kommentert denne artikkelen ennå.