
Newtons andre lovsøknader, eksperimenter og øvelser
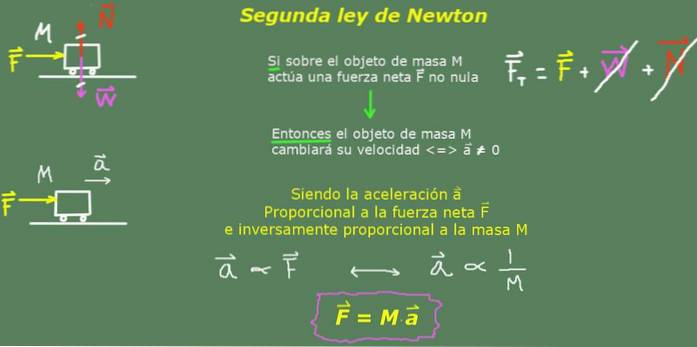
De andre lov av Newton eller den grunnleggende dynamikken i loven fastslår at hvis et objekt utsettes for en kraft eller et sett med krefter som ikke avbryter, vil objektet akselerere i retning av den resulterende kraften, og denne akselerasjonen er proporsjonal med intensiteten til nettokraften og omvendt proporsjonal med massen til objektet.
Ja F er nettokraften, M massen av objektet og til akselerasjonen den får, så ville Newtons andre lov uttrykkes matematisk slik: til = F / M eller på den vanligste måten F = M∙til
Artikkelindeks
- 1 Forklaring og formler
- 2 Løst øvelser
- 2.1 Øvelse 1
- 2.2 Øvelse 2
- 3 Anvendelser av Newtons andre lov
- 3.1 Akselerasjonen av en heis
- 3.2 Majonesburken
- 4 Eksperimenter for barn
- 4.1 Eksperiment 1
- 4.2 Eksperiment 2
- 5 Artikler av interesse
- 6 Referanser
Forklaring og formler
Som forklart ovenfor er den vanlige måten å uttrykke den andre loven på med formelen:
F = M∙til
Både akselerasjon og kraft må måles fra en treghetsreferanseramme. Merk at massen er en positiv størrelse, så akselerasjonen peker i samme retning som den resulterende kraften.
Legg også merke til at når den resulterende kraften er null (F = 0) da vil akselerasjonen også være null ( til = 0 ) så lenge som M> 0. Dette resultatet stemmer helt overens med Newtons første lov eller treghetslov.
Newtons første lov etablerer treghetsreferansesystemer som de som beveger seg med konstant hastighet i forhold til en fri partikkel. I praksis og for de vanligste applikasjonene, vil et referansesystem festet til bakken eller noe annet som beveger seg med konstant hastighet i forhold til det, betraktes som treghet..
Kraft er det matematiske uttrykket for objektets interaksjon med miljøet. Kraften kan være en konstant mengde eller endre seg med tiden, posisjonen og hastigheten til objektet..
Enheten i det internasjonale systemet (SI) for styrke er Newton (N). Massen i (SI) måles i (kg) og akselerasjonen i (m / s)to). En kraftstyrke er den kraften som er nødvendig for å akselerere et objekt med en masse på 1 kg ved 1 m / sto .
Løst øvelser
Øvelse 1
Et objekt med masse m frigjøres fra en viss høyde og en fallakselerasjon på 9,8 m / s² måles.
Det samme skjer med et annet objekt med masse m 'og et annet med masse m "og et annet og et annet. Resultatet er alltid tyngdekraftens akselerasjon som er betegnet med g og er lik 9,8 m / s². I disse eksperimentene er formen på objektet og verdien av massen er slik at kraften på grunn av luftmotstand er ubetydelig.
Det blir bedt om å finne en modell for jordens attraktive kraft (kjent som vekt) som er i samsvar med eksperimentelle resultater..
Løsning
Vi velger et treghetsreferansesystem (fast i forhold til bakken) med en positiv retning av den vertikale X-aksen og nedover.
Den eneste kraften som virker på masseobjektet m er jordens tiltrekningskraft, den kraften kalles vekten P, hvordan det peker ned er positivt.
Akselerasjonen som masseobjektet får m når den er utgitt, er den det a = g , påpekt og positiv.
Vi foreslår Newtons andre lov
P = m a
Hva vil være modellen for P slik at akselerasjonen som den andre loven forutsier er g uavhengig av verdien av m? : Det eneste alternativet er at P = m g når m> 0.
m g = m a hvorfra vi fjerner: a = g
Vi konkluderer med at vekten, kraften som Jorden tiltrekker seg med et objekt, vil være massen til objektet multiplisert med tyngdekraftens akselerasjon, og dens retning er vertikal og pekt ned.
P = m∙g
Øvelse 2
En blokk på 2 kg masse hviler på et helt flatt og horisontalt gulv. Hvis en kraft på 1 N påføres den, hva er akselerasjonen til blokken og hvilken hastighet den vil ha etter 1 s.
Løsning
Det første er å definere et treghetskoordinatsystem. En er valgt med X-aksen på gulvet og Y-aksen vinkelrett på den. Deretter lages et kraftdiagram som plasserer kreftene på grunn av interaksjonen mellom blokken og omgivelsene.

Kraften N representerer det normale, det er den vertikale oppadgående kraften som gulvoverflaten utøver på blokken M. Det er kjent at N nøyaktig balanserer P fordi blokken ikke beveger seg i vertikal retning.
F er den horisontale kraften som påføres blokk M, og peker i positiv retning av X-aksen.
Nettokraften er summen av alle kreftene på masseblokken M. Vi lager vektorsummen av F, P og N. Siden P og N er like og motsatte, avbryter de hverandre, og nettokraften er F.
Så den resulterende akselerasjonen vil være kvotienten til nettokraften og massen:
a = F / M = 1 N / 2 kg = 0,5 m / s²
Når blokken starter fra hvile etter 1s, vil hastigheten ha endret seg fra 0 m / s til 0,5 m / s .
Anvendelser av Newtons andre lov
Akselerere heis
En gutt bruker en badevekt for å måle vekten. Verdien du får er 50 kg. Så tar gutten vekten til heisen til bygningen sin, fordi han vil måle heisens akselerasjon. Resultatene oppnådd ved oppstart er:
- Vekten registrerer en vekt på 58 kg i 1,5 s
- Mål deretter 50 kg igjen.
Med disse dataene beregner du akselerasjonen til heisen og hastigheten den oppnår.
Løsning
Vekten måler vekten i en enhet som heter kilogram_styrke. Per definisjon er kilogramstyrken den kraften som planeten Jorden tiltrekker seg med et objekt med en masse på 1 kg.
Når den eneste kraften som virker på gjenstanden er dens vekt, får den en akselerasjon på 9,8 m / s². Så 1 kg_f tilsvarer 9,8 N.
Vekten P av gutten er da 50 kg * 9,8m / s² = 490 N
Under akselerasjon utøver skalaen en kraft N på gutten på 58 kg_f tilsvarer 58 kg * 9,8 m / s² = 568,4 N.
Akselerasjonen av heisen vil bli gitt av:
a = N / M - g = 568,4 N / 50 kg - 9,8 m / s² = 1,57 m / s²
Hastigheten som er oppnådd av heisen etter 1,5 s med akselerasjon på 1,57 m / s² er:
v = a * t = 1,57 m / s² * 1,5 s = 2,36 m / s = 8,5 Km / t
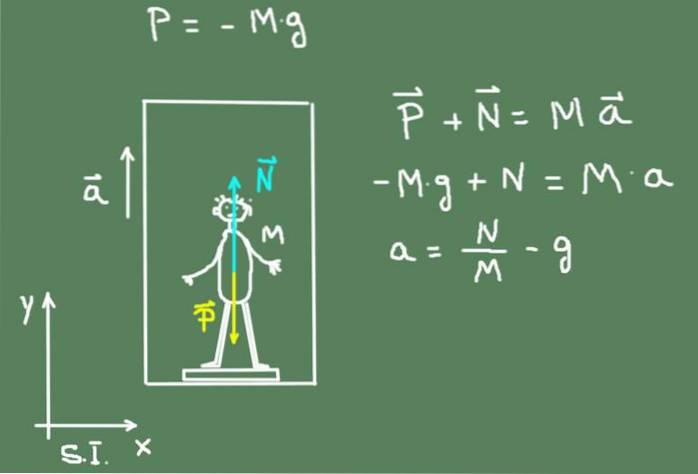
Følgende figur viser et diagram over kreftene som virker på gutten:
Majonesburken
En gutt gir broderen majonesburken til broren, som er i den andre enden av bordet. For det kjører den den på en slik måte at den får en hastighet på 3 m / s. Fra det øyeblikket flasken ble sluppet til den stoppet i motsatt ende av bordet, var kjøringen 1,5 m.
Bestem verdien av friksjonskraften som bordet utøver på flasken, vel vitende om at den har en masse på 0,45 kg.
Løsning
Først skal vi bestemme bremseakselerasjonen. For dette vil vi bruke følgende forhold, allerede kjent fra den jevnt akselererte rettlinjede bevegelsen:
Vf² = Vi² + 2 * a * d
hvor Vf er den endelige hastigheten, Sag starthastighet, til akselerasjon og d forskyvningen.
Akselerasjonen oppnådd fra det forrige forholdet er, hvor forskyvningen av flasken har blitt tatt som positiv.
a = (0 - 9 (m / s) ²) / (2 * 1,5 m) = -3 m / s²
Nettokraften på majonesburken er friksjonskraften, siden den normale og vekten av krukken balanserer: Fnet = Fr.
Fr = m * a = 0,45 kg * (-3 m / s²) = -1,35 N = -0,14 kg-f
Eksperimenter for barn
Barn og voksne kan utføre enkle eksperimenter som lar dem bekrefte at Newtons andre lov virkelig fungerer i det virkelige liv. Her er to veldig interessante:
Eksperiment 1
Et enkelt eksperiment krever baderomsvekt og heis. Ta en vekt på badet i en heis og registrer verdiene den markerer under oppstart, nedstart og i løpet av tiden du beveger deg i konstant hastighet. Beregn heisakselerasjonene for hvert tilfelle.
Eksperiment 2
- Ta en lekebil som har hjulene godt smurt
- Fest et tau til enden.
- Teip en blyant eller et annet glatt, sylindrisk objekt som strengen vil passere over, ved kanten av bordet..
- I den andre enden av tauet, heng en liten kurv som du vil plassere noen mynter på eller noe som tjener som vekt..
Skjemaet for eksperimentet er vist nedenfor:
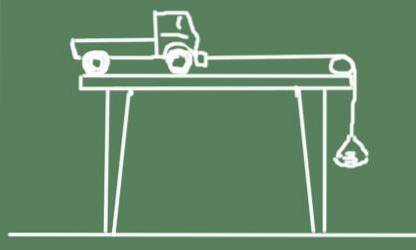
- Slipp vognen og se den få fart.
- Øk deretter vognens masse ved å plassere mynter på den, eller noe som øker vekten..
- Si om akselerasjonen øker eller avtar. Legg mer deig på vognen, se at den akselererer og avslutt.
Vognen blir deretter igjen uten ekstra vekt og får lov til å akselerere. Deretter legges mer vekt på kurven for å øke kraften som blir påført vognen..
- Sammenlign akselerasjonen med forrige tilfelle, indiker om den øker eller avtar. Du kan gjenta å legge til mer vekt i kurven og observere akselerasjonen i vognen.
- Angi om den øker eller avtar.
- Analyser resultatene dine og si om de er enige med Newtons andre lov.
Artikler av interesse
Eksempler på Newtons andre lov.
Newtons første lov.
Eksempler på Newtons andre lov.
Referanser
- Alonso M., Finn E. 1970. Fysikk bind I: Mekanikk. Interamerikansk utdanningsfond S.A. 156-163.
- Hewitt, P. 2012. Konseptuell fysikk. Femte utgave. 41-46.
- Young, Hugh. 2015. Universitetsfysikk med moderne fysikk. 14. utg. Pearson. 108-115.



Ingen har kommentert denne artikkelen ennå.